0. 들어가며
오늘은 본격적으로 Linear Regression Model (선형회귀모델)에 대하여 알아보고자 한다.
1. Linear Regression Model 개요
Linear Regression Model은 출력변수 Y를 입력변수 X들의 Linear Combination으로 표현한 모델이다.
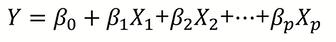
Linear Combination(선형결합)은 변수들을 상수배와 (+), (-)를 통해 결합하는 것을 의미한다.
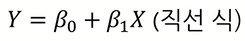
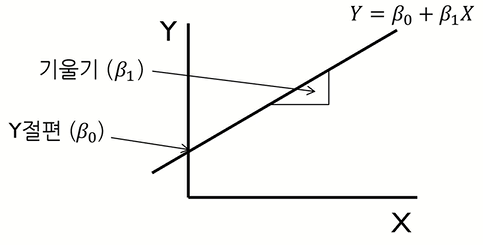
예를 들어, X변수 1개가 Y변수 1개를 표현하는 경우는 위와 같은 식으로 나타낼 수 있을 것이고, 해당 식은 직선이므로 위와 같이 그릴 수 있다.
결국, Linear Regression Model 의 목적은 2가지이다.
- X변수와 Y변수 사이의 관계를 수치로 설명
- 미래의 반응변수 Y값을 예측
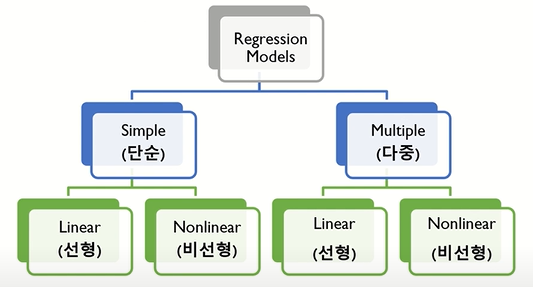
Linear Regression Model 은 위와 같이 나눌 수 있는데,
X변수의 수가 1개면 Simple, 2개 이상이면 Multiple로 구분된다.
또한 X변수와 Y변수의 선형성 여부에 따라 각각 Linear, Nonlinear로 구분된다.
2. Linear Regression Model 가정
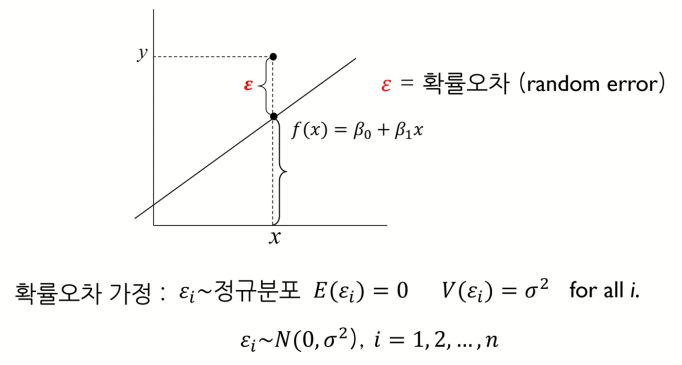
Linear Regression Model 을 구축하기 위해 필요한 한 가지 가정에 대하여 알아보겠다.
우선 ε 이 의미하는 것은 Error라고 지난 포스팅에서 언급했었다. Linear Regression Model 은 ε 은 정규분포를 따른다는 가정하에 설명이 된다.
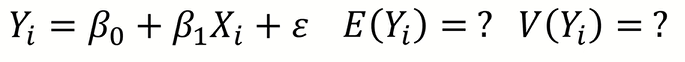
ε 이 정규분포를 따르기 때문에 결국 Y도 정규분포를 따른다는 것을 알 수 있다.
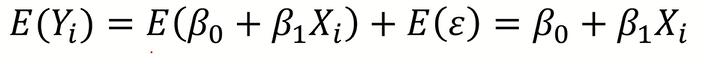
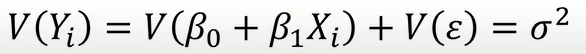
Y의 Mean값과 Variance값을 구하면 위와 같다.
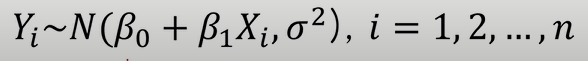
따라서 Y도 위와 같은 정규분포를 따름을 알 수 있다.
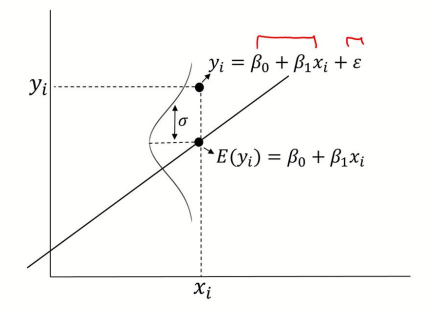
그렇다면 출력변수 Y가 특정값이 아닌 확률분포를 따르는데 X와 Y의 관계를 어떻게 추론할 수 있을까?
결론부터 말하자면, 입력변수 X와 출력변수 Y의 평균 ( E(Y) )과의 관계 를 설명하는 선형식을 찾으면 된다.
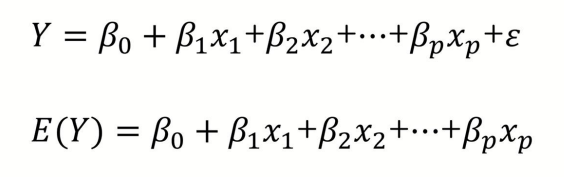
E(Y)를 구하면 확률분포를 따르는 ε 이 사라지고 f(X)만 남기 때문에 E(Y)는 확률분포를 따르지 않고 특정값으로 산출되기 때문이다.
3. 마치며
오늘은 Linear Regression Model 에 관한 간단한 개요와 가정을 알아보았다.
- Linear Regression은 X와 Y의 선형결합으로 이루어짐
- Linear Regression에서의 출력변수 Y는 정규분포를 따르기 때문에 X와 Y평균과의 관계를 추론 해야 함
다음 포스팅에서는 parameter B0, B1을 추정하는 방법과 Linear Regression에서 주로 사용하는 최적화(optimization) 기법에 대하여 알아보겠다.
또한 필자는 고려대학교 김성범 교수님이 운영하시는 유튜브 채널을 보고 공부한 내용을 포스팅 하였으므로 아래 출처를 남긴다.
https://www.youtube.com/@user-yu5qs4ct2b
