0. 들어가며
지난 포스팅에서 Linear Regression Model 의 기본 개념과 가정에 대해 알아보았다.
아래를 보고 다시 복기해보자.
- Linear Regression은 X와 Y의 선형결합으로 이루어짐
- Linear Regression에서의 출력변수 Y는 정규분포를 따르기 때문에 X와 Y평균과의 관계를 추론 해야 함
오늘은 Linear Regression Model 의 parameter를 추정하는 방법에 대하여 알아보고자 한다.
1. Parameter 추정
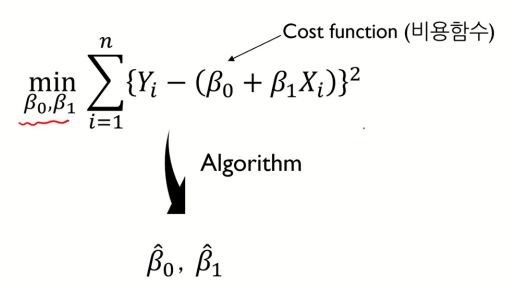
우리의 목표는 Cost function 이 최소가 되도록 하는 B0와 B1 을 구하는 것이다.
이때, 특정 알고리즘을 이용하여 구한 B0와 B1값을 각각 B̂0, B̂1 이라고 한다.
cf) 기호 위에 모자처럼 그려진 hat 기호는 실제값이 아닌 계산한 예측값이라는 의미로 주로 사용
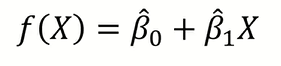
그렇게 구한 parameter값을 대입하면 우리의 모델은 위와 같은 식으로 쓸 수 있을 것이다.
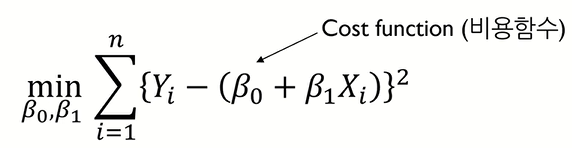
다시 본론으로 돌아와서, 우리의 목표는 Cost function 이 최소가 되도록 하는 parameter를 구하는 것이다.
이때, Cost function 이 어떻게 생겼는지에 따라서 parameter를 구하는 방법의 난이도가 달라진다.
다행히도 Linear Regression Model 에서의 parameter 추정은 쉽게 구할 수 있는데, 그 이유는 Cost function 의 형태가 Convex 하기 때문이다.
Convex function의 특징 중 하나는 아래와 같다.
- Cost function is convex -> globally optimal solution exists (전역 최적해 존재)
전역 최적해가 존재하기 때문에 우리는 Cost function 을 미분해서 값이 0이 되는 B0와 B1을 구하기만 한다면 Cost function 이 최소가 되는 parameter를 구할 수 있는 것이다.
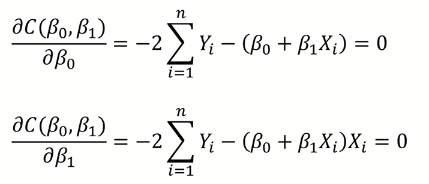
따라서 Cost function 을
- B0에 대해서 미분한 값이 0이 되게 하는 식
- B1에 대해서 미분한 값이 0이 되게 하는 식
총 2개의 식을 세워서 연립을 하여 풀 수 있다.
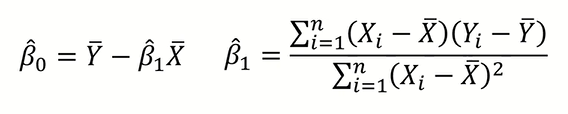
연립을 하면 위와 같은 값이 나온다.
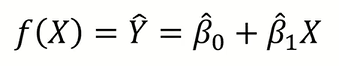
따라서 결국 위와 같은 모델을 구하였다.
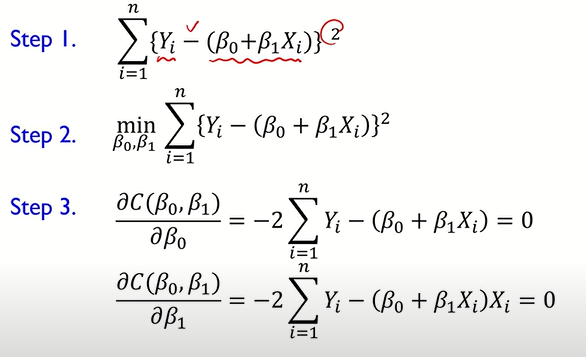
parameter 추정 알고리즘을 요약하자면
- Cost function을 구한다.
- Cost function이 최소가 되도록 하는 B0와 B1을 구한다.
- B0와 B1에 대하여 각각 미분한다.
(Cost function의 기울기가 0인 지점에서 최소를 가지기 때문)
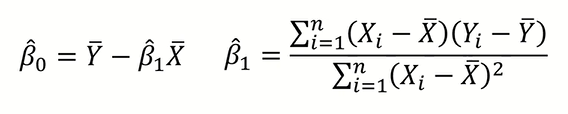
중요!!!
위와 같은 방식으로 Linear Regression Model 에서 B0과 B1을 구하는 알고리즘을 LSE(Least Squares Estimation)이라 한다.
2. 잔차(Residual)
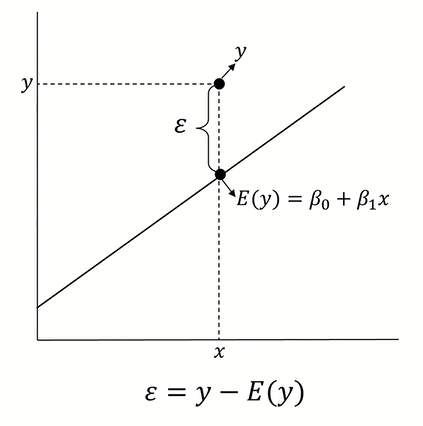
우리는 이전에 ε 은 Error를 의미하고 정규분포를 따른다는 가정을 배웠다.
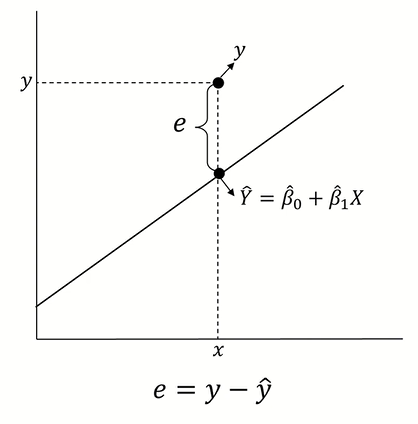
잔차(Residual) 은 확률오차 ε 이 실제로 구현된 값으로 정규분포를 따르는 것이 아닌 실제 값을 의미한다.
3. 마치며
오늘은 Linear Regression Model 에서의 parameter 추정 방법인 LSE(Least Square Estimation) 알고리즘과 잔차(Residual) 에 대해서 알아보았다.
다음 포스팅에서는 Logistic Regression Model 에 대하여 알아볼 예정이다.
또한 필자는 고려대학교 김성범 교수님이 운영하시는 유튜브 채널을 보고 공부한 내용을 포스팅 하였으므로 아래 출처를 남긴다.
https://www.youtube.com/@user-yu5qs4ct2b
