[ML] 머신러닝 학습 과정

박건·2023년 8월 23일

[ML] Machine Learning

목록 보기

4/10

지난 포스팅에서는 수치형 데이터 와 범주형 데이터 에 대해서 알아보았다.

이번에는 Machine Learning 의 전체적인 학습 과정에 대하여 기술하고자 한다.

위의 이미지를 보면 다변량 데이터는 다음과 같이 X와 Y로 나눌 수 있고, 각각 (독립변수, 종속변수) 혹은 (입력변수, 출력변수) 로 불리운다고 일전에 언급한 적이 있다.

만약 X변수가 Y변수에 어떤 영향을 주는지를 정확하게 우리가 알고있다면 새로운 데이터 X가 들어왔을 때 어떤 출력이 나올지 예상할 수 있을 것이다.

핵심 아이디어는 X와 Y의 관계를 찾는 것.

예측하려는 대상인 Y를 설명하는 여러 개의 X변수를 이용

X변수를 조합하여 Y를 표현

수학적으로는 Y = f(X1, X2, X3, X4, ... , Xn)

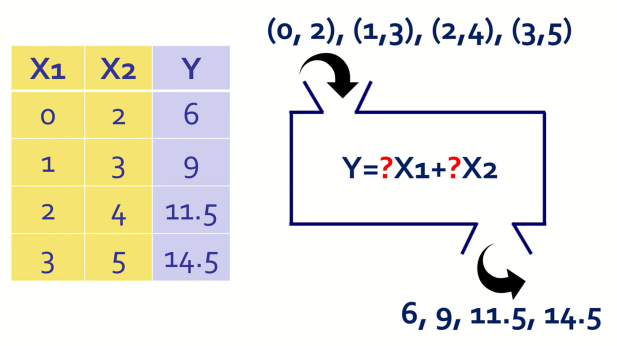
다음과 같은 데이터가 주어진다면 우리의 목표는 X와 Y가 수학적으로 어떤 관계가 있는지를 알아내는 것이다.

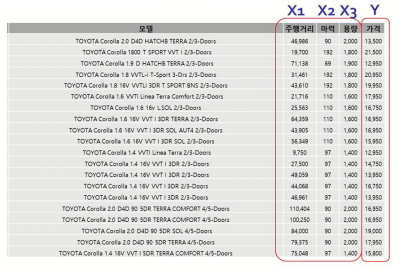
실제로 위와 같은 중고차 모델 데이터가 주어진다면

이를 수학적으로 표현하면 아래와 같다.

뒤에 적혀있는 ε 은 입실론이라고 읽고, 여기서는 X로 설명할 수 없는 부분. 쉽게 말하자면 Error를 의미한다.

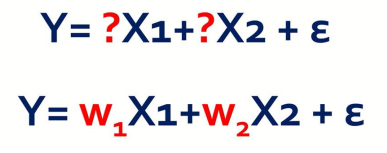
앞에서 보았던 수식에서 ?를 수학적 기호로 w1, w2 로 쓰게 되면 위 사진과 같다.

그렇다면 우리에게 주어진 것은 Y, X1, X2이므로 w1, w2만 구할 수 있다면 Y값을 예측할 수 있다

이때, w1과 w2를 모델의 parameter 라고 하고, 다시 말해서 모델의 parameter w1과 w2 를 구한다면 우리가 원하는 결과를 얻을 수 있다는 뜻이다.

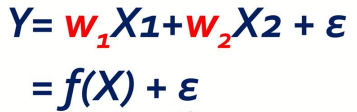
수식을 Y에 대해서 다시 정리하면 X에 대한 함수 f(X)와 그렇지 않은 ε으로 나타낼 수 있다.

이를 ε 에 대해서 정리하면 위와 같고, 이것이 의미하는 것은 Error(오차) 이다.

Error 가 0이 된다면 모델 f(X)는 완벽한 모델임을 의미하고, 따라서 우리의 목표는 ε 을 가장 작게 만드는 것이다.

실제로 우리는 수많은 데이터 Sample을 사용하여 모델을 학습하기 때문에 Sample의 수가 총 n개 있을 때 각각의 X, Y 데이터에 대한 식은 위처럼 나타낼 수 있을 것이다.

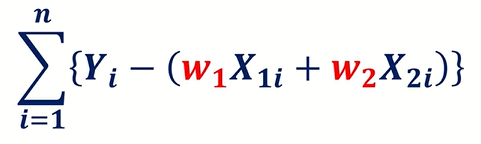
따라서 모든 Sample에 대하여 각 데이터의 ε 을 Summation한 수식은 위와 같다.

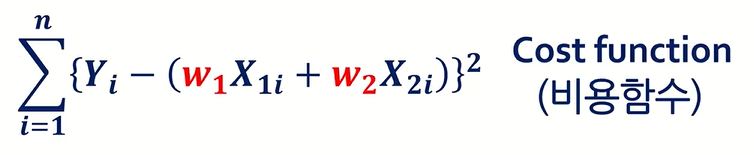
여기서 중요한 점은 일반적으로 ε 을 최소로 만들기 위한 식을 세울 때, 제곱을 취한 값을 Summation하여 사용한다.
제곱을 취한 값이 여러가지로 학습에 효율적이기 때문인데 그 이유는 다음과 같다.

위와 같은 식을 Cost function 이라고 부르고, Loss function 이라고도 불리우므로 두 가지 표현 모두 알고 있는 것이 좋다.

정리하자면 Machine Learning 은 결국 Cost function 이 최소가 되도록 모델을 학습 시키는 과정을 거치는 것이다.

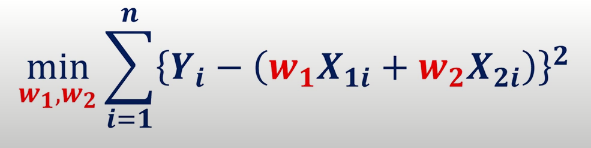
결국 Cost function 을 최소가 되도록 하기 위한 w1과 w2를 찾아야 하는 문제로 귀결된다. (Y, X1, X2값은 이미 우리가 알고있는 상수이다.)

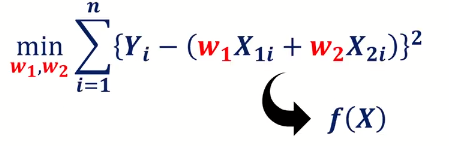
지금까지는 다중선형회귀 모델을 예로 들어서 설명하였지만, 실제 Machine Learning 에는 수많은 모델이 존재한다.
그리고 각각의 Model parameter (w1, w2...)를 추정하는 방법 또한 제각각이다.

다중선형회귀모델을 사용할 때는 LSE(Least Square Estimation) 라는 방법을 통하여 Model parameter를 추정
로지스틱회귀모델 을 사용할 때는 Conjugate Gradient 라는 방법을 통하여 Model parameter를 추정
뉴럴네트워크모델 을 사용할 때는 Backpropagation 이라는 방법을 통하여 Model parameter를 추정

최종적으로 Machine Learning 모델의 학습 과정을 요약하자면 다음과 같다.