(2573) 빙산 (Java)

문제

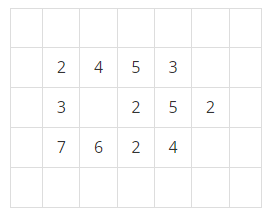
지구 온난화로 인하여 북극의 빙산이 녹고 있다. 빙산을 그림 1과 같이 2차원 배열에 표시한다고 하자. 빙산의 각 부분별 높이 정보는 배열의 각 칸에 양의 정수로 저장된다. 빙산 이외의 바다에 해당되는 칸에는 0이 저장된다. 그림 1에서 빈칸은 모두 0으로 채워져 있다고 생각한다.

그림 1. 행의 개수가 5이고 열의 개수가 7인 2차원 배열에 저장된 빙산의 높이 정보

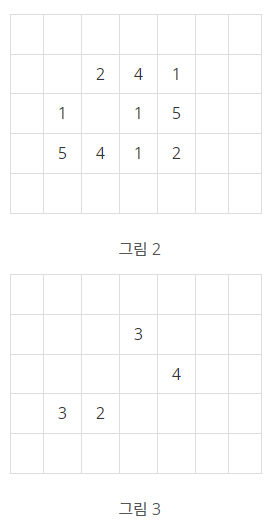
빙산의 높이는 바닷물에 많이 접해있는 부분에서 더 빨리 줄어들기 때문에, 배열에서 빙산의 각 부분에 해당되는 칸에 있는 높이는 일년마다 그 칸에 동서남북 네 방향으로 붙어있는 0이 저장된 칸의 개수만큼 줄어든다. 단, 각 칸에 저장된 높이는 0보다 더 줄어들지 않는다. 바닷물은 호수처럼 빙산에 둘러싸여 있을 수도 있다. 따라서 그림 1의 빙산은 일년후에 그림 2와 같이 변형된다.

그림 3은 그림 1의 빙산이 2년 후에 변한 모습을 보여준다. 2차원 배열에서 동서남북 방향으로 붙어있는 칸들은 서로 연결되어 있다고 말한다. 따라서 그림 2의 빙산은 한 덩어리이지만, 그림 3의 빙산은 세 덩어리로 분리되어 있다.

한 덩어리의 빙산이 주어질 때, 이 빙산이 두 덩어리 이상으로 분리되는 최초의 시간(년)을 구하는 프로그램을 작성하시오. 그림 1의 빙산에 대해서는 2가 답이다. 만일 전부 다 녹을 때까지 두 덩어리 이상으로 분리되지 않으면 프로그램은 0을 출력한다.

입력

첫 줄에는 이차원 배열의 행의 개수와 열의 개수를 나타내는 두 정수 N과 M이 한 개의 빈칸을 사이에 두고 주어진다. N과 M은 3 이상 300 이하이다. 그 다음 N개의 줄에는 각 줄마다 배열의 각 행을 나타내는 M개의 정수가 한 개의 빈 칸을 사이에 두고 주어진다. 각 칸에 들어가는 값은 0 이상 10 이하이다. 배열에서 빙산이 차지하는 칸의 개수, 즉, 1 이상의 정수가 들어가는 칸의 개수는 10,000 개 이하이다. 배열의 첫 번째 행과 열, 마지막 행과 열에는 항상 0으로 채워진다.

출력

첫 줄에 빙산이 분리되는 최초의 시간(년)을 출력한다. 만일 빙산이 다 녹을 때까지 분리되지 않으면 0을 출력한다.

예제 입력 1

5 7
0 0 0 0 0 0 0
0 2 4 5 3 0 0
0 3 0 2 5 2 0
0 7 6 2 4 0 0
0 0 0 0 0 0 0

예제 출력 1

2

출처

Olympiad > 한국정보올림피아드 > KOI 2006 > 초등부 2번

잘못된 데이터를 찾은 사람: occidere, zayne

알고리즘 분류

구현
그래프 이론
그래프 탐색
너비 우선 탐색
깊이 우선 탐색

Solution

import java.io.*;
import java.util.LinkedList;
import java.util.Queue;
import java.util.StringTokenizer;

public class Main {
    public static int n, m, area, year;
    public static boolean isIceburg;
    public static int[][] iceburg;
    public static boolean[][] visited;
    public static int[] dx = {-1, 1, 0, 0};
    public static int[] dy = {0, 0, -1, 1};
    public static class Node {
        int x, y;
        Node(int x, int y) {
            this.x = x;
            this.y = y;
        }
    }
    public static Queue<Node> q;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        StringTokenizer st = new StringTokenizer(br.readLine());

        n = Integer.parseInt(st.nextToken());
        m = Integer.parseInt(st.nextToken());
        iceburg = new int[n][m];
        q = new LinkedList<Node>();

        for(int i = 0; i < n; i++) {
            st = new StringTokenizer(br.readLine());
            for(int j = 0; j < m; j++) {
                iceburg[i][j] = Integer.parseInt(st.nextToken());
            }
        }

        year = -1;   // 경과 년수 초기화, (빙산의 area를 카운트하는 시점이 그 빙산이 세팅이 된 다음 턴이므로)

        // 빙산이 2덩어리가 되거나, 0으로 없어질때까지 반복
        while(countArea() == 1);

        if(isIceburg) bw.write(String.valueOf(year));
        else bw.write("0");

        bw.flush();
        bw.close();
        br.close();
    }

    public static int countArea() {
        isIceburg = false;  // 빙산 유무 flag
        area = 0;   // 덩어리 수 초기화
        visited = new boolean[n][m];    // 방문처리 초기화

        for(int i = 0; i < n; i++) {
            for(int j = 0; j < m; j++) {
                // 빙산이 아니거나, 이미 방문한 빙산이면 skip
                if(iceburg[i][j] <= 0 || visited[i][j]) continue;

                // 빙산이 있으면 flag true
                isIceburg = true;

                // 영역 +1
                area++;

                q.offer(new Node(i, j));
                visited[i][j] = true;

                while(!q.isEmpty()) {
                    Node curNode = q.poll();

                    int cnt = 0;
                    for(int k = 0; k < 4; k++) {
                        int nx = curNode.x + dx[k];
                        int ny = curNode.y + dy[k];

                        // 노출 면의 수 구하기, 해당 년도에 빙산이었던 경우는 제외해야하므로 방문 여부도 체크
                        if(iceburg[nx][ny] <= 0 && !visited[nx][ny]) cnt++;

                        // 바다 범위를 벗어나거나, 바다이거나, 이미 방문한 빙산이면 skip
                        if(isNotRange(nx, ny) || iceburg[nx][ny] <= 0 || visited[nx][ny]) continue;

                        // 다음 탐색 칸 큐에 넣고, 방문처리
                        q.offer(new Node(nx, ny));
                        visited[nx][ny] = true;
                    }

                    // 현재 칸의 노출 면수에 따라 높이 차감
                    iceburg[curNode.x][curNode.y] -= cnt;
                }
            }
        }

        // +1년 경과
        year++;

        // 빙산이 없을때 까지 2덩어리가 되지 못했으므로
        if(!isIceburg) return 0;
        else return area;
    }

    public static boolean isNotRange(int x, int y) {
        return (x < 0 || x >= n || y < 0 || y >= m) ? true : false;
    }
}

Feedback

1. 빙산이 녹으면서 0 미만으로 떨어지는 경우가 있을 수 있기 때문에, '빙산이 아니다' 라는 조건을 따질때 0보다 작거나 같은 경우로 따져줘야 한다.
2. 한 턴(1년)을 탐색하는 중간에 빙산이 녹아 바다가 되는 경우도 있기 때문에, 시작점을 잡을때 빙산이 아닌 경우만 continue를 할게 아니라, 방문여부도 따져줘야 한다. (해당 턴에 빙산이 녹아서 바다가 된 경우를 빙산이 아닌 경우로 인식하여 continue 시켜버릴 수 있기 때문)