(2146) 다리 만들기 (Java)
| 시간 제한 | 메모리 제한 | 제출 | 정답 | 맞힌 사람 | 정답 비율 |
|---|---|---|---|---|---|
| 2 초 | 192 MB | 36988 | 13559 | 8414 | 33.506% |
문제
여러 섬으로 이루어진 나라가 있다. 이 나라의 대통령은 섬을 잇는 다리를 만들겠다는 공약으로 인기몰이를 해 당선될 수 있었다. 하지만 막상 대통령에 취임하자, 다리를 놓는다는 것이 아깝다는 생각을 하게 되었다. 그래서 그는, 생색내는 식으로 한 섬과 다른 섬을 잇는 다리 하나만을 만들기로 하였고, 그 또한 다리를 가장 짧게 하여 돈을 아끼려 하였다.
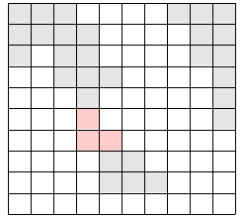
이 나라는 N×N크기의 이차원 평면상에 존재한다. 이 나라는 여러 섬으로 이루어져 있으며, 섬이란 동서남북으로 육지가 붙어있는 덩어리를 말한다. 다음은 세 개의 섬으로 이루어진 나라의 지도이다.
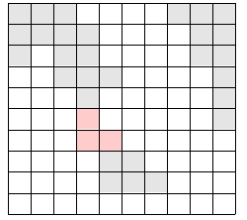
위의 그림에서 색이 있는 부분이 육지이고, 색이 없는 부분이 바다이다. 이 바다에 가장 짧은 다리를 놓아 두 대륙을 연결하고자 한다. 가장 짧은 다리란, 다리가 격자에서 차지하는 칸의 수가 가장 작은 다리를 말한다. 다음 그림에서 두 대륙을 연결하는 다리를 볼 수 있다.
물론 위의 방법 외에도 다리를 놓는 방법이 여러 가지 있으나, 위의 경우가 놓는 다리의 길이가 3으로 가장 짧다(물론 길이가 3인 다른 다리를 놓을 수 있는 방법도 몇 가지 있다).
지도가 주어질 때, 가장 짧은 다리 하나를 놓아 두 대륙을 연결하는 방법을 찾으시오.
입력
첫 줄에는 지도의 크기 N(100이하의 자연수)가 주어진다. 그 다음 N줄에는 N개의 숫자가 빈칸을 사이에 두고 주어지며, 0은 바다, 1은 육지를 나타낸다. 항상 두 개 이상의 섬이 있는 데이터만 입력으로 주어진다.
출력
첫째 줄에 가장 짧은 다리의 길이를 출력한다.
예제 입력 1
10
1 1 1 0 0 0 0 1 1 1
1 1 1 1 0 0 0 0 1 1
1 0 1 1 0 0 0 0 1 1
0 0 1 1 1 0 0 0 0 1
0 0 0 1 0 0 0 0 0 1
0 0 0 0 0 0 0 0 0 1
0 0 0 0 0 0 0 0 0 0
0 0 0 0 1 1 0 0 0 0
0 0 0 0 1 1 1 0 0 0
0 0 0 0 0 0 0 0 0 0
예제 출력 1
3
출처
빠진 조건을 찾은 사람: choiking10
데이터를 추가한 사람: hello70825, ohyuni
잘못된 데이터를 찾은 사람: tncks0121
알고리즘 분류
그래프 이론
그래프 탐색
너비 우선 탐색
Solution
import java.io.*;
import java.util.LinkedList;
import java.util.Queue;
import java.util.StringTokenizer;
public class Main {
public static int n, min;
public static int[][] cntr;
public static boolean[][] visited;
public static class Node {
int x, y, dis;
Node(int x, int y, int dis) {
this.x = x;
this.y = y;
this.dis = dis;
}
}
public static Queue<Node> q;
public static int[] dx = {-1, 1, 0, 0};
public static int[] dy = {0, 0, -1, 1};
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st;
n = Integer.parseInt(br.readLine());
cntr = new int[n][n];
visited = new boolean[n][n];
q = new LinkedList<Node>();
// 나라 세팅
for(int i = 0; i < n; i++) {
st = new StringTokenizer(br.readLine());
for(int j = 0; j < n; j++) {
cntr[i][j] = Integer.parseInt(st.nextToken());
}
}
// 섬마다 넘버링
numberingIsland();
// 방문 초기화 및 최단 거리 초기화
visited = new boolean[n][n];
min = Integer.MAX_VALUE;
// 최단 다리 길이 구하기
for(int i = 0; i < n; i++) {
for(int j = 0; j < n; j++) {
if(cntr[i][j] == 0 || visited[i][j]) continue;
// 다리 최단 거리 찾기
findDistance(i, j, cntr[i][j]);
// 다음 섬 탐색을 위한 방문 초기화
visited = new boolean[n][n];
}
}
bw.write(String.valueOf(min));
bw.flush();
bw.close();
br.close();
}
public static void numberingIsland() {
int num = 0;
for(int i = 0; i < n; i++) {
for(int j = 0; j < n; j++) {
if(visited[i][j] || cntr[i][j] == 0) continue;
num++;
q.offer(new Node(i, j, 0));
cntr[i][j] = num;
visited[i][j] = true;
while(!q.isEmpty()) {
Node cur = q.poll();
for(int k = 0; k < 4; k++) {
int nx = cur.x + dx[k];
int ny = cur.y + dy[k];
if(isNotRange(nx, ny) || visited[nx][ny] || cntr[nx][ny] == 0) continue;
q.offer(new Node(nx, ny, 0));
cntr[nx][ny] = num;
visited[nx][ny] = true;
}
}
}
}
}
public static void findDistance(int i, int j, int num) {
q = new LinkedList<Node>();
q.offer(new Node(i, j, 0));
visited[i][j] = true;
while(!q.isEmpty()) {
Node cur = q.poll();
for(int k = 0; k < 4; k++) {
int nx = cur.x + dx[k];
int ny = cur.y + dy[k];
// 인접 칸이 나라의 범위를 벗어나거나, 이미 방문했으면 skip
if(isNotRange(nx, ny) || visited[nx][ny]) continue;
// 인접 칸이 현재 칸과 같은 섬이면 방문처리 후 skip
if(cntr[nx][ny] == num) {
visited[nx][ny] = true;
continue;
}
// 인접 칸이 바다일 경우 큐에 넣고, 방문처리 (거리 계산 +1)
if(cntr[nx][ny] == 0) {
q.offer(new Node(nx, ny, cur.dis+1));
visited[nx][ny] = true;
}
// 인접 칸이 현재 섬과 다른 섬인 경우 최단거리 비교
else if(cntr[nx][ny] != 0 && cntr[nx][ny] != num) {
min = Math.min(min, cur.dis);
return;
}
}
}
}
public static boolean isNotRange(int x, int y) {
return (x < 0 || x >= n || y < 0 || y >= n) ? true : false;
}
}Feedback
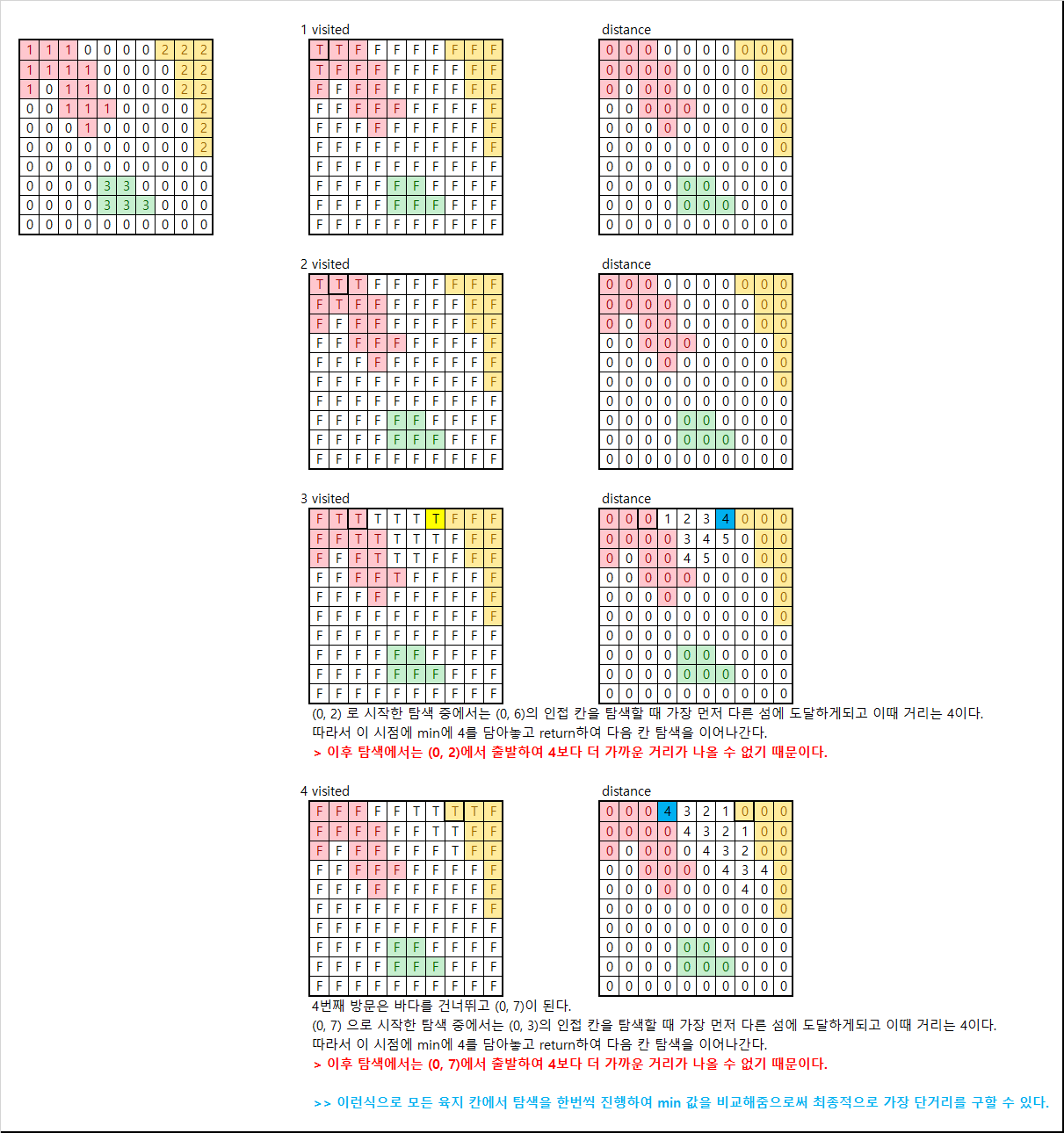
- 섬마다 넘버링을 하여 서로 다른 섬이라는 것을 구분지어 주어야 섬 사이의 거리를 계산해낼 수 있다.
- 각 육지칸을 탐색하며, 가장 짧은 거리를 구해서 min에 담고, 비교하고, 담고의 과정을 반복한다.
- 이때 초기 min 값을 바보같이 n 으로 잡았다.. 그럴거면 n*n으로 잡아야했는데, 다음부터 이런 경우에는 그냥 Integer.MAX_VALUE를 사용하자.