[DNN] Weight Initialization

가중치 초기화의 중요성

가중치 초기화는 딥러닝 모델이 학습을 시작할 때의 출발점을(초기 값) 의미하며, 이 값들이 모델의 학습 및 minimum cost 수렴 동작에 영향을 미칩니다.

만약 모든 가중치를 0으로 초기화하면 역전파 과정에서 모든 뉴런이 동일한 기울기(gradient)를 가지게 되어, 네트워크가 대칭성 문제에 빠지고 학습이 어려워집니다. 또한, 초기 가중치가 너무 크거나 작으면 기울기(gradient)가 너무 커지거나 작아져서 기울기(gradient) 폭주나 소실 문제가 발생할 수 있습니다.

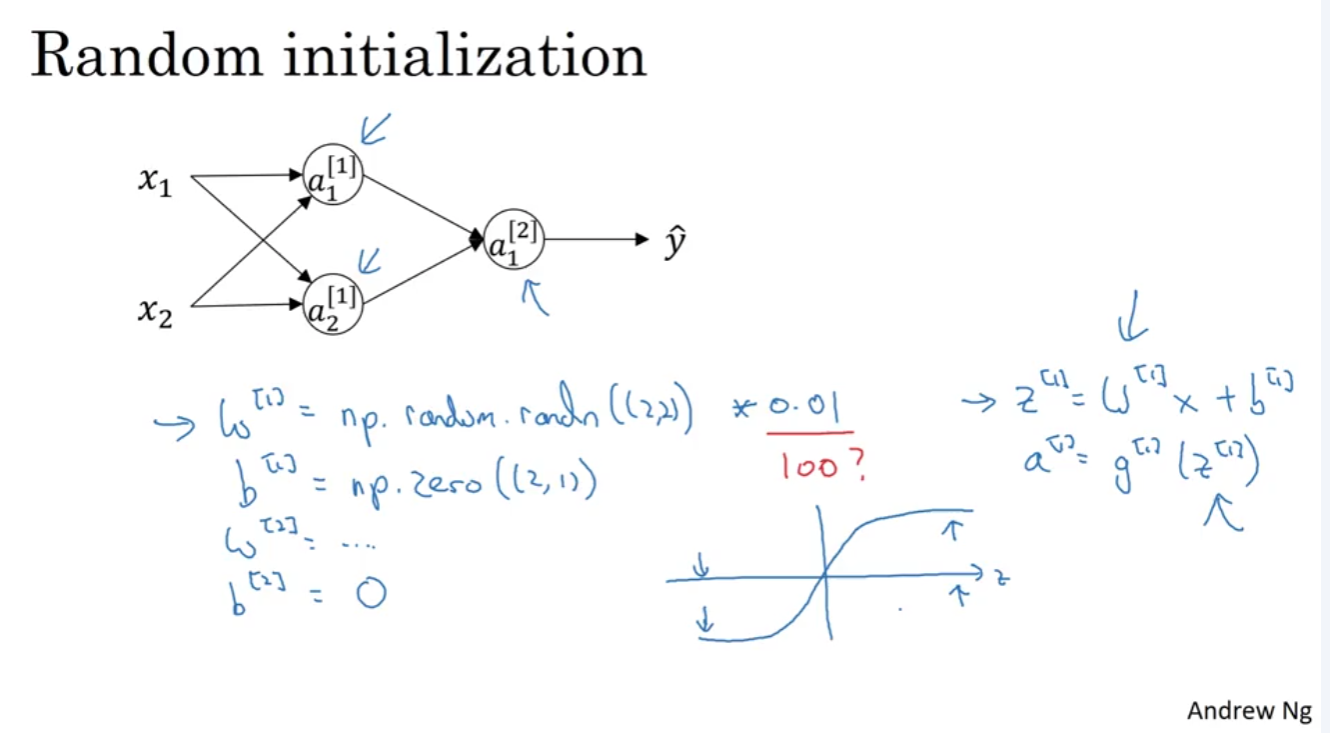
Zero Initialization

• a1과 a2가 완전히 동일한 output을 계산하게되므로 layer의 node를 여러개 두는게 의미가 없으며, 학습이 진행되지 않음.

Constant Initialization

• 신경망의 가중치를 0이 아닌 상수로 초기화하면 같은 계층에 있는 뉴런은 마치 하나의 뉴런만 있는 것처럼 작동함.

Random Initialization

• 만약 Weight를 크게 설정하면 Sigmoid/Tanh function을 통과할 때 0 또는 1에 가까운 값을 출력하게 되는데, 이 부분은 굉장히 평평한 부분이라서 기울기가 굉장히 작음. 따라서 학습이 엄청 느려지게 됨.
• 따라서 Weight는 0.01 과 같은 작은 숫자를 곱해서 작게 만들어주는게 기본임.

He initialization and Xavier initialzation

• Make usre the weights are 'just right', not too small, not too big.

※ see [DNN] Vanishing and exploding gradients first.

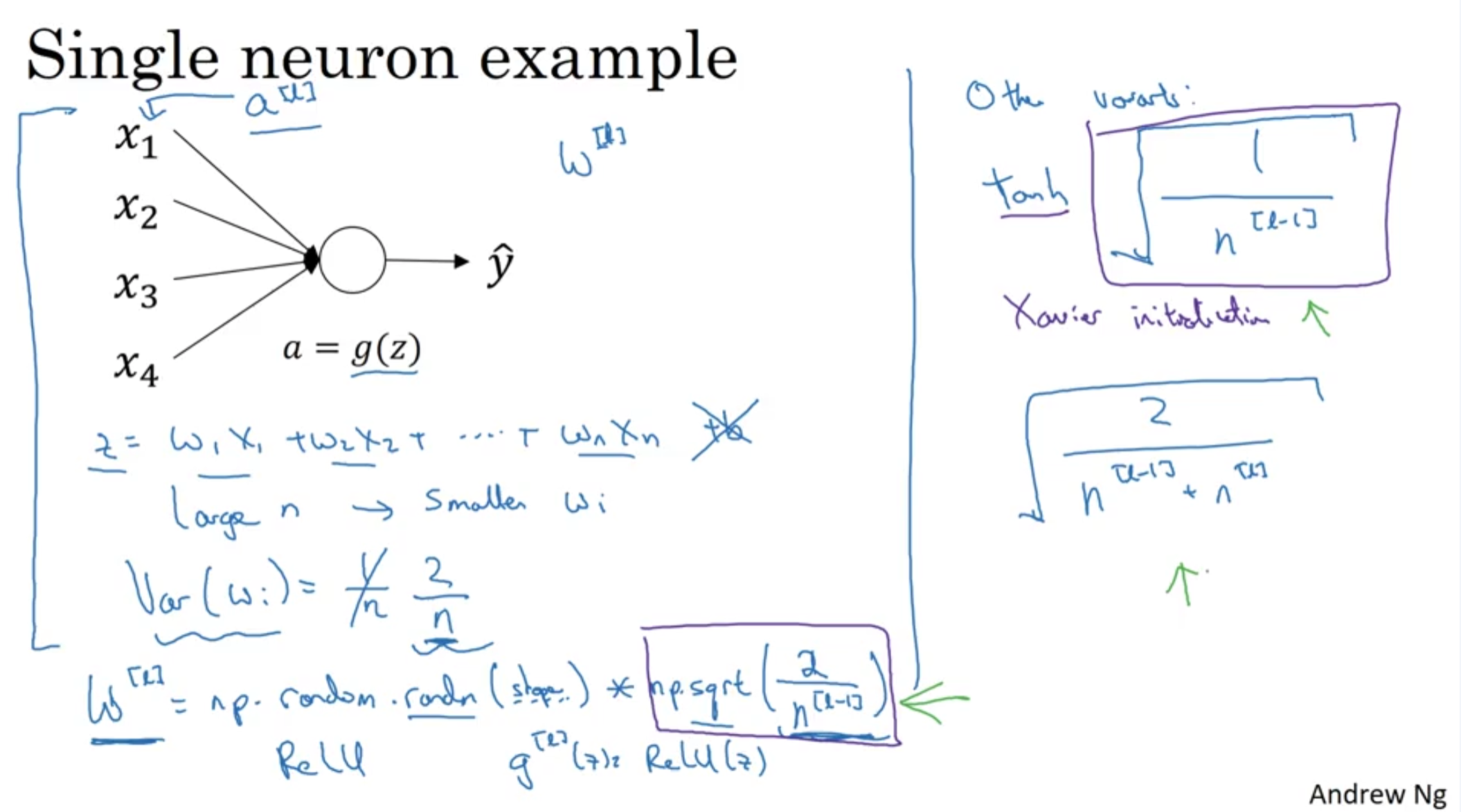
• Z is the sum of w * x.
• so if n is large, you want smaller wi in order to prevent exploding.
• One reasonable approach is multiplying the variance of wi which is 1/n when initializing the matrix.

For relu: W[l] = np.random.randn(shape) np.sqrt(2/n^[l-1]) < He
For tanh: W[l] = np.random.randn(shape) np.sqrt(1/n^[l-1]) < Xavier initialization
there are other methods as well.