추천시스템 문헌조사(CB, CF, MF, NCF, AutoRec)

대표적인 문제

cold start

• 유저 혹은 아이템에 대한 정보가 없는 상태에서 시작해 추천의 정확도가 떨어지는 문제
• 예를들어 넷플릭스에 처음 가입한 상태가 있다. 아직 시청 기록도 평가 기록도 없으므로 추천을 하기 어렵다.

sparsity dataset

• 아이템이 너무 많아서 유저가 사용한 경험이 있는 아이템의 수 는 그 중에서 극히 일부 밖에 되지 않는다. 즉, 유저-아이템 행렬을 만들었을 때, 0이 되는 부분이 엄청 많아지게 된다.

long tail

• 전체 추천 아이템으로 보이는 비율이 ‘사용자들의 관심을 많이 받은 소수의 아이템'으로 구성되어 있는 ‘비대칭적 쏠림 현상’이 발생하는 문제

Content-Based Recommender systems(CB)

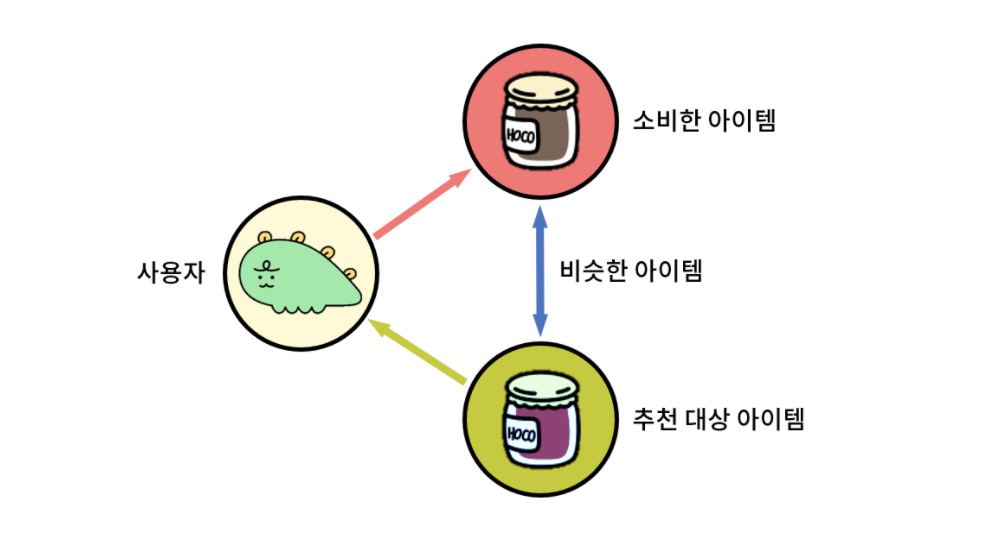
• 유저가 좋은 평가한 영화와 유사한 영화 추천

	감독	배우1	배우2	장르	등등…
영화1
영화2

• 이렇게 있을때 영화1과 영화2의 유사도를 구할 수 있다.
• 영화를 시청한 유저의 feature도 영화의 feature를 계속 쌓아서 만들 수 있다. 그 결과 유저의 feature도 만들 수 있고 유저간의 유사도도 구할 수 있다.

1. 장점
   • 유저의 취향 변화를 빠르게 적용할 수 있다.
2. 단점
   • item에 대한 정보가 많을수록 추천 정확도가 높아지는 구조라 필요한 정보량이 많다.
   • cold start problem

Collaborative Filtering-based recommender system(CFB)

1. Memory-based collaborative filtering
   • 추천 결과를 모두 메모리에 올려 놓고 사용
   • 추천 속도가 매우 빠름
   • 개별 사용자에게 맞춘 추천이 가능
   • 대용량 데이터에서 속도 저하 이슈
   • sparse 한 데이터에서 성능 저하 이슈
2. Model-based collaborative filtering
   • 데이터를 활용해 모델을 만들어 놓고 추천하는 방식
   • 최적화나 매개변수 학습 활용
   • sparse한 데이터에서 성능이 상대적으로 좋음
   • 결과 설명력이 낮음

Memory-based collaborative filtering

user based CF

• 유저간의 유사도를 계산하여 유사도가 높은 유저가 본 영화중 평점이 높은 영화를 추천하는 방식이다.
• 즉, 나와 비슷한 성향의 유저를 찾는다. → 그 유저가 높게 평가한 내가 보지 않은 아이템을 추천한다.
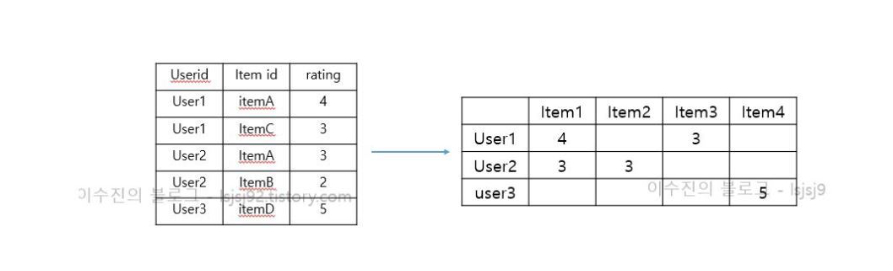
• 사용자 아이템 행렬에서 사용자가 아직 평가하지 않은 아이템을 예측하는 것이 목표

algorithm

1. user X와 선호, 불호가 유사한 user A를 찾는다. X는 A의 neighbourhood라고 부른다.
   1. 유사한 userA는 대표적으로 cosine similarity를 사용해 찾을 수 있다.
2. X가 가장 선호할것같은 item들이 A에게 추천된다.

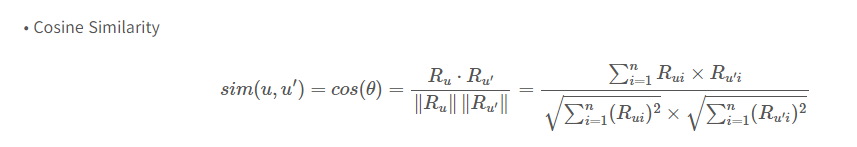
장점

• 최적화나 훈련 과정이 필요 없다.
• 접근 방식이 쉽고 성능이 좋은 편이다.

단점

• sparse matrix의 경우 성능이 많이 저하된다.
• 여전히 cold start 문제가 있다.
• long tail 문제 : 점점 더 편향될 확률이 높다.
• 대용량 데이터의 경우 계산 결과값을 메모리에 계속 올려놔야한다는 문제
• 또한 유저 아이템이 많으면 계산량이 많아진다는 문제
• 유저와 아이템이 확장될 때마다 새로 계산해야함

Model-based collaborative filtering

memory based CF 의 문제

• sparse matrix의 경우 성능이 많이 저하된다.
• 유저와 아이템이 확장될 때마다 새로 계산해야함

이 두 가지 문제를 해결하기 위해 등장한 것이 Matrix Factorization(MF)

행렬분해의 다양한 기법 활용가능

• Orthogonal Factorization(Singular Vector Decomposition(SVD) 특이값 분해 )
• Non-Negative Matrix Factorization(NMF)
• Probabilistic Factorization(PMF) 등

Matrix Factorization(SVD)

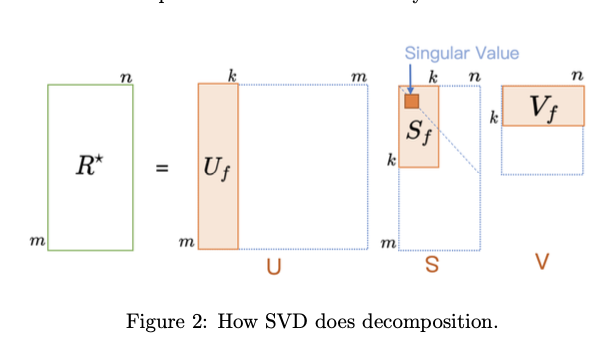
• 초기에는 많이 알려진 수학적 모델인 svd와 같은 행렬 분해 방법을 사용했다.
• 분해를 하고 차원을 축소하여 복원하면 관측되지 않은 rating 값을 예측할 수 있다.
• 문제는 sparse data에 대해서 대처가 투박했다는 점이다.
  • 평균값을 넣고 계산하는 방식으로 활용

Laten Factor Model(Funk-SVD)

• 본격적으로 laten factor를 학습하는 방식이 활용
• 딥러닝적 접근

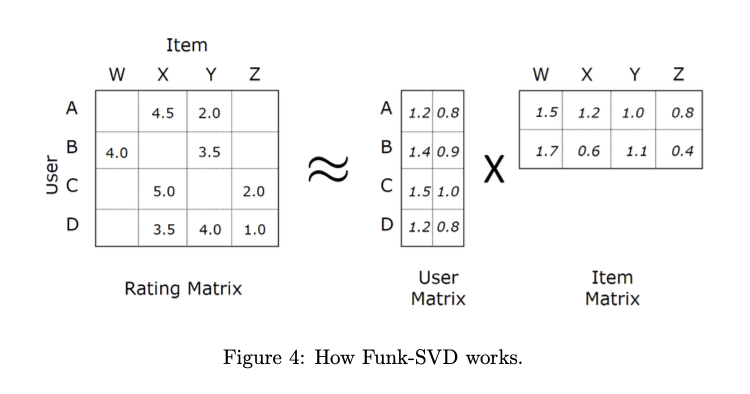
• user, item → one-hot encoding
• $P_u, Q_i = latent\,vecotr$
• $\bold{v}_u,\, \bold{v}_i = one-hot\, vector$

$\hat{r}*{ui}=\Sigma*{f=1}^{F}{p_{uf}q_{if}}=P^T\bold{v}^{U}_u \cdot Q^T\bold{v}^{I}_i$

Loss Function

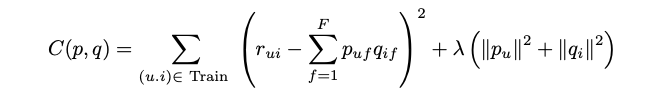
• overfitting 방지를 위한 l2 정규화

장점

• 모델만 만들어 놓으면 바로바로 계산해서 결과를 도출할 수 있어서 메모리 부담이 적음

단점

• 선형모델이라 설명력이 부족함

Factorization Machine (FM)

• 유저와 아이템간의 특성 벡터를 학습하는 것이 아니라 유저-아이템을 묶은 특성을 학습
• high sparsity data 에서도 잘 작동한다.

Deep Learning based Matrix Factorization

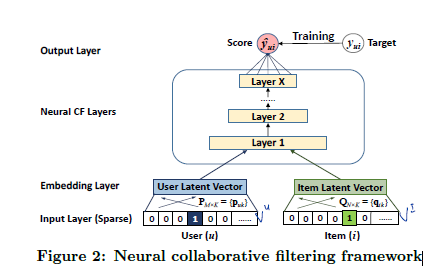
장점

• MF model에 비선형성을 넣어 더 복잡한 관계를 표현할 수 있다
• 기존 MF 모델보다 정확도가 높다.

Neural Collaborative Filtering

GMF

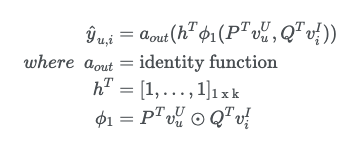
• 저자는 MF는 NCF의 특별한 케이스이며 이를 GMF라고 칭한다.

• GMF란 $a_{out}$(non-linear function)과 $h^{T}$(weight)를 아래와 같이 둔다.

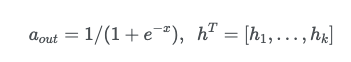
MLP

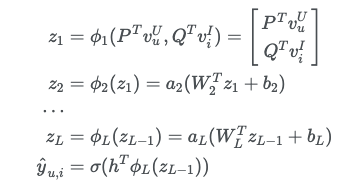
• mlp를 사용하면 복잡한 비선형 관계를 표현할 수 있다고 한다.
• rating 뿐만 아니라 다양한 implict action들을 학습할 수 있다.

GMF + MLP

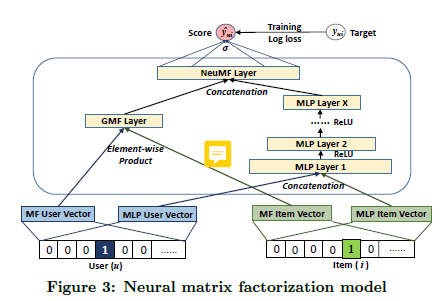
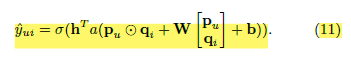
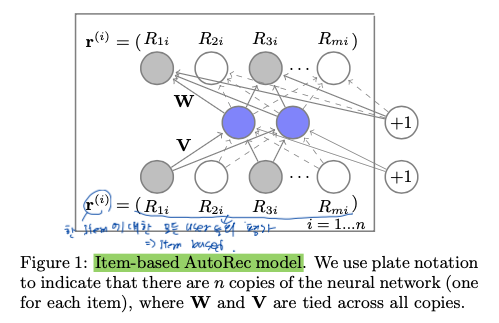
AutoRec

• AutoEncoder 구조를 사용해 user-item rating matrix를 reconstriction 한다.
• 이 과정에서 관측되지 않은 rating 값이 예측된다.

RMSE

• 일반적인 CF 모델에 비해 계산량이 적지만 성능은 크게 뒤쳐지지 않는다.
• mf모델과 달리 user(혹은 item)만 latent space로 embed 한다.

추천시스템 평가 방법

Precision/Recall@K (기본적인 방법)

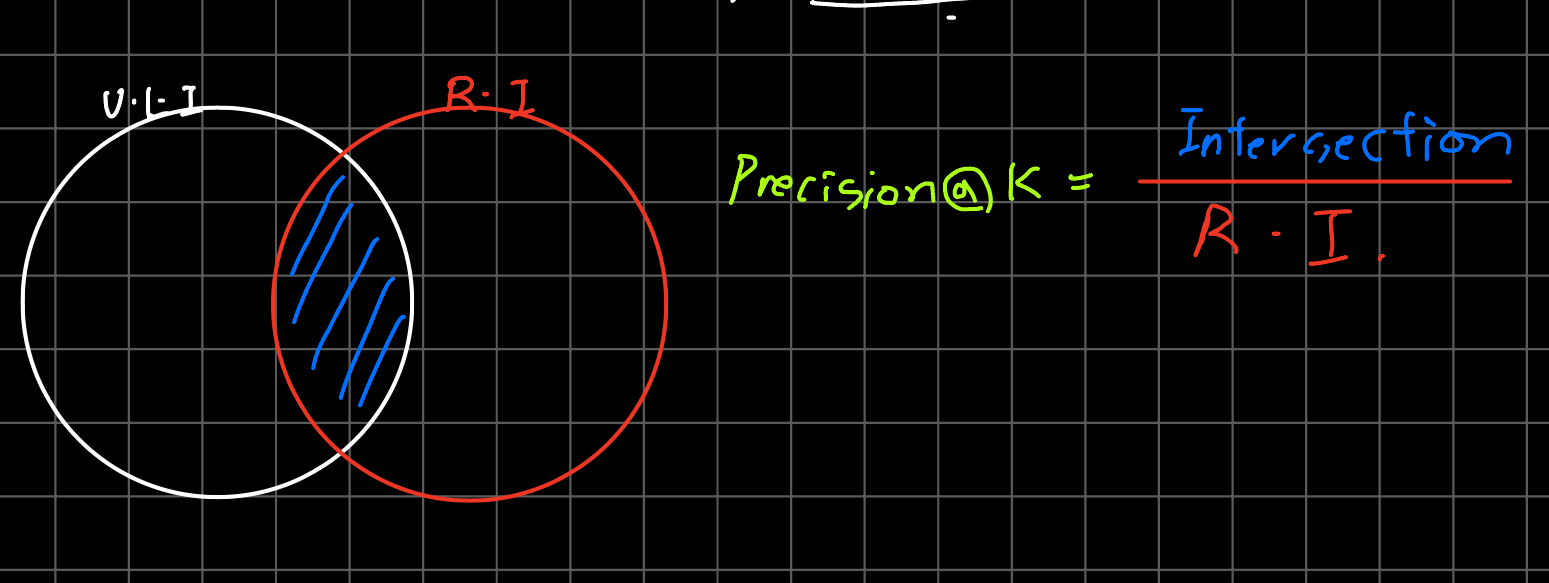
Precision@K

• 내가 추천한 K개의 item 중에 소비자의 관심에 있던 item은 몇 개 인가?
• 예를들어 내가 5개의 item을 추천했을 때 소비자가 그 중 3개를 좋아했다면

⇒ $Precision@K = \frac{R\cap U}{R}= \frac{3}{5} = 0.6$

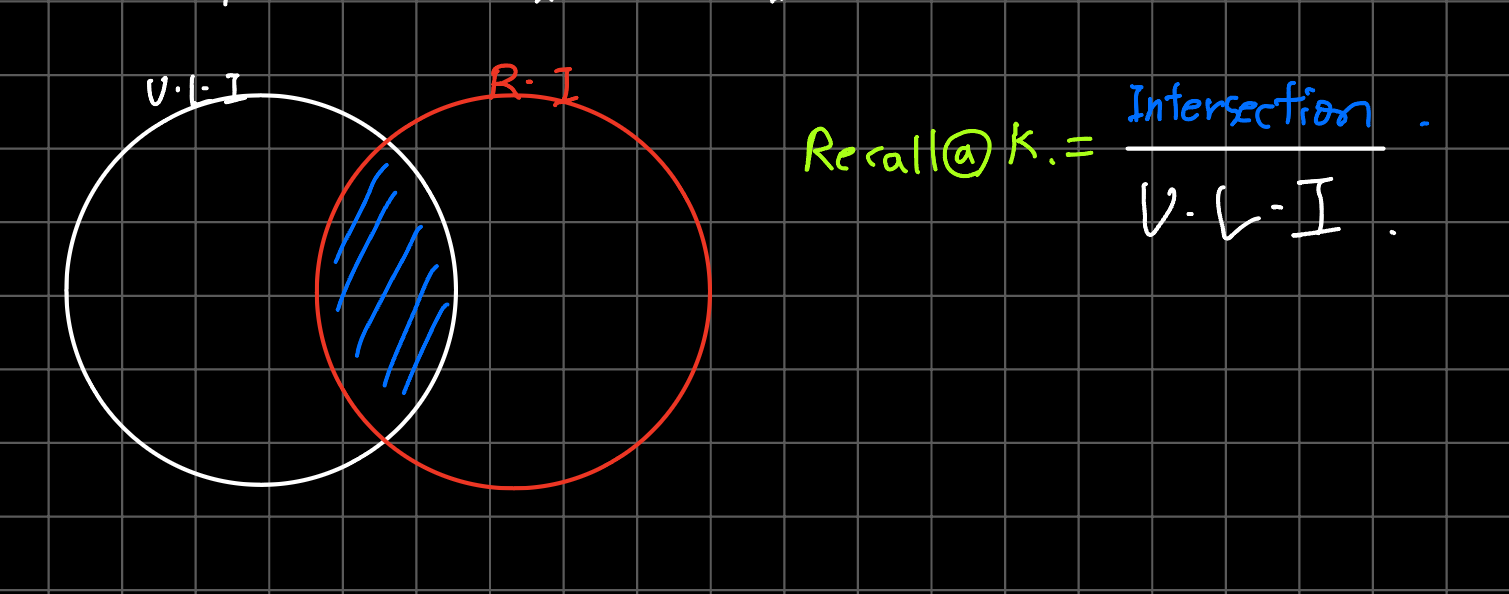
Recall@K

• 사용자가 좋아하는 item중에 내가 추천한 K개의 item이 몇 개나 포함이 되어있나?
• 예를들어 소비자가 좋아요를 눌러 놓은 아이템이 5일 때, 내가 추천한 아이템 중 2개가 거기에 포함되어 있다면

⇒ $Recall@K = \frac{R\cap U}{U}= \frac{2}{5} = 0.4$

Mean Average Precision@K

• precision, recall과 달리 추천 순서를 고려한 평가 지표
• mean (average precision)으로 average precision의 mean 값이다.

Average Precision@K

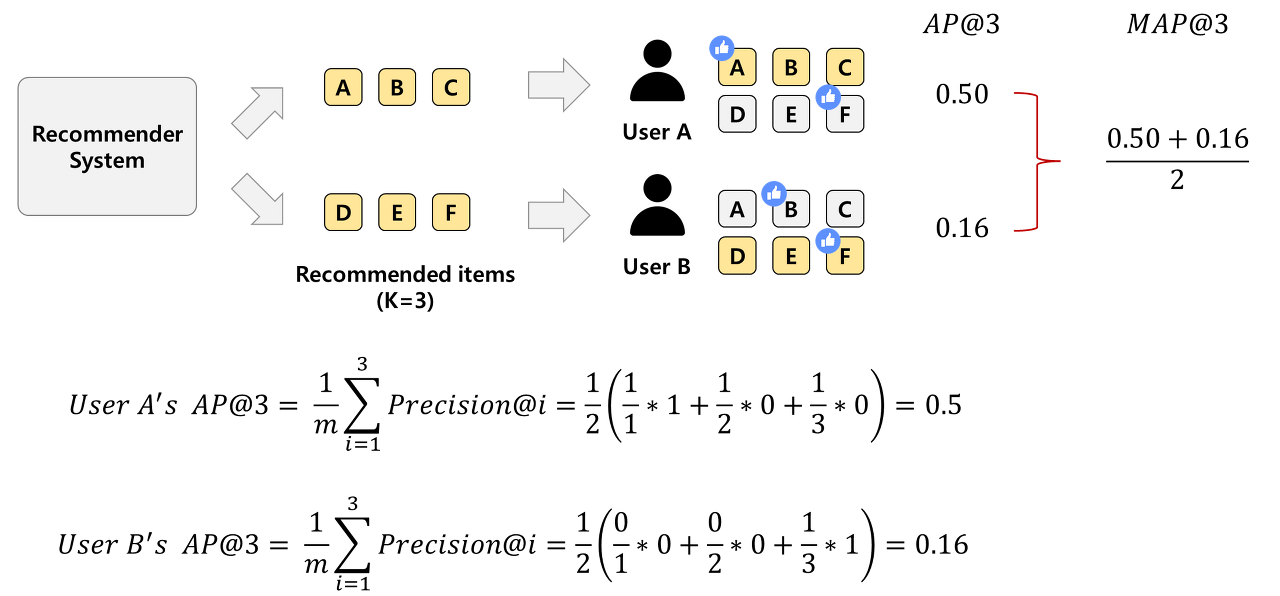
• $Precision@i$는 K개의 추천 중에서 i까지만 고려한 precision 값
• 예를들어 A를 계산할때는 1추천한 것 중에 1개 맞음, B를 추천했을때는 2개 추천 중에 1개 맞음 이런식

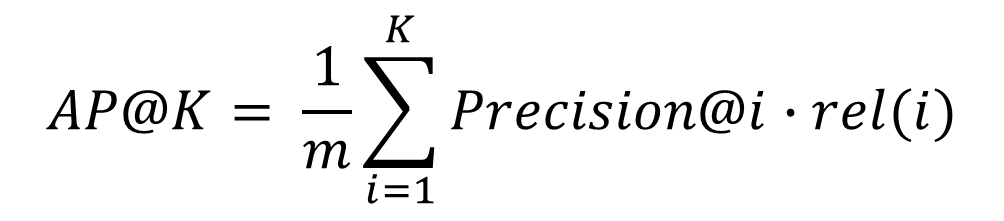
• $rel(i)$는 i번 째 item을 좋아하는지 아닌지 여부이다. binary value로 {0, 1}로 표현된다.

Mean Average Precision@K

• $MAP@K는 AP@K$의 평균

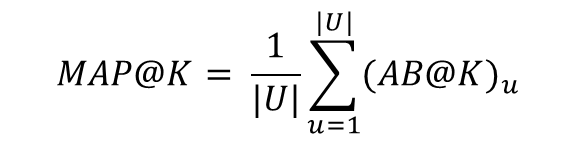
NDCG@K (Normalized Discounted Cumulative Gain)

• 원래 NDCG는 검색 분야에서 사용되던 지표지만 추천 시스템에도 많이 사용
• MAP는 추천 리스트 중 어떤 순서에 포함 되었는지(rel(i)) 여부만 반영 되지만 $NDCG@K$는 순서에 $MAP@K$보다 민감하게 가중치를 두고 계산한다.

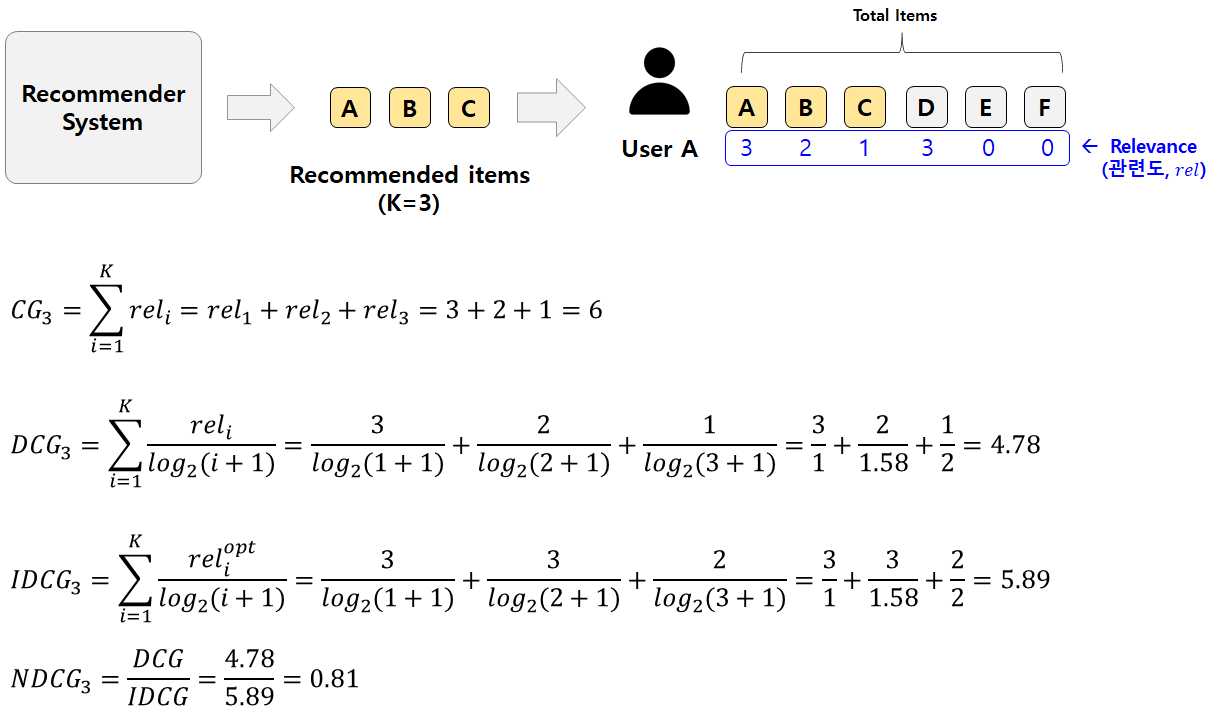
Relevance

• 사용자가 특정 아이템과 얼마나 관련이 있는지 나타내는 값
• 예를들어 신발 추천인 경우 사용자가 해당 신발을 얼마나 클릭 했는지 등으로 선정할 수 있다.

Cumulative Gain(CG)

• 추천한 아이템의 relevance 합

  

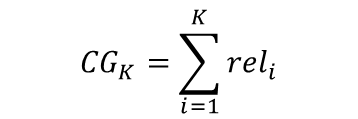
Discounted Cumulative Gain (DCG)

• 순서에 따른 할인 개념 도입
• 추천 순서가 뒤로 갈수록 분모가 커져 영향을 적게 받는다.
• 문제는 사용자별로 추천 아이템의 수가 다른 경우 정확한 성능 평가가 어렵다는 한계점이 존재한다. 추천 아이템의 수가 많아질수록 DCG 값은 증가하기 떄문에, 정확한 평가를 위해서는 scale을 맞춰야 한다.

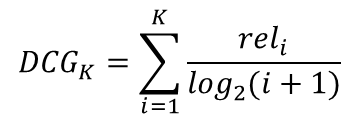
Normalized DCG (NDCG)

• 앞선 DCG의 문제인 추천 아이템이 많을 수록 값이 증가한다는 점을 보완하기 위해 정규화를 적용한 DCG이다.

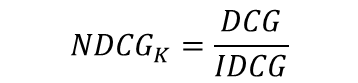
• IDCG는 최선의 추천을 했을 때 받을 수 있는 DCG 값이다.

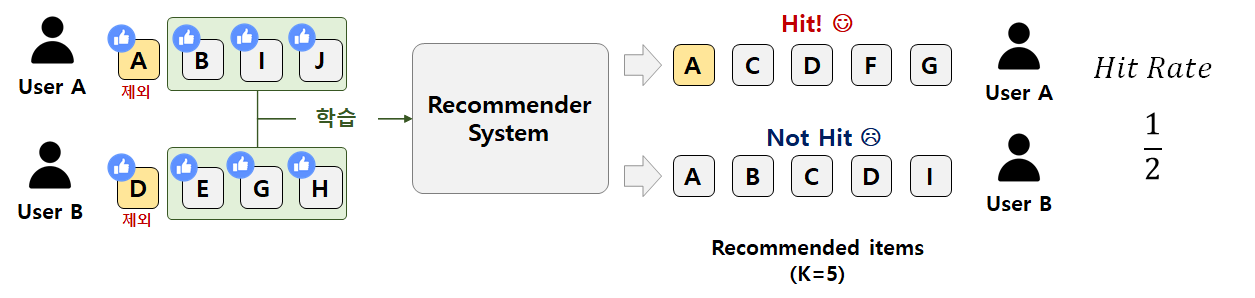
Hit Rate@K

• 전체 사용자 수 대비 적중한 사용자 수를 의미한다. (적중률)

1. 사용자가 선호한 아이템 중 1개를 제외한다.
2. 나머지 아이템들로 추천 시스템을 학습한다.
3. 사용자별로 K개의 아이템을 추천하고, 앞서 제외한 아이템이 포함되면 Hit이다.
4. 전체 사용자 수 대비 Hit한 사용자 수 비율을 구하면 Hit Rate가 된다.

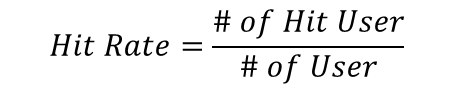
MAE & RMSE

• 평점 예측에 적합한 평가 방법

MAE

• 단순 평균 이기 때문에 이상치에 쉽게 영향을 받는다.

RMSE

• 제곱을 하기 때문에 1미만의 오차는 작아지고 1이상의 오차는 더 크게 반영된다.

Reference

• https://tech.kakao.com/2021/12/27/content-based-filtering-in-kakao/
• https://lsjsj92.tistory.com/563
• An Introduction to Matrix factorization and Factorization Machines in Recommendation System, and Beyond
• A systematic review and research perspective on recommender systems
• https://leehyejin91.github.io/post-ncf/
• https://kmhana.tistory.com/31
• https://users.cecs.anu.edu.au/~akmenon/papers/autorec/autorec-paper.pdf
• https://sungkee-book.tistory.com/11