[Paper Review]Deep Weakly-supervised Anomaly Detection

1. PURPOSE

• weakly supervised learning은 우리가 anomaly label을 불완전하게 가지고 있다고 가정한다. 이러한 가정에서 두 가지 문제를 해결하고자 한다.
• 해당 논문은 1번 문제인 작은 양의 anomaly data문제를 해결하기 위해 pairwise augment 방법을 제시한다.

2. CONTENTS

Intorduction

• anomaly detection(AD)의 목표는 예외적인 data instance를 찾고 정의하는 것이다.
• 문제는 anomaly data를 labeling 하는 것에 비용이 매우 많이 발생하고, 데이터에 noise나 unintersting isolated data 들이 anomaly로 섞여 있어서 detection error가 많다.
• 최근 semi-supervised AD method들은 단지 supervised-learning과 unsupervised-learning을 연결하기 위한 방법으로만 사용되었다.
• 문제는 이러한 방법들이 small anomaly dataset에서 설명할 수 있는 anomaly data에만 초점이 맞춰져 있다는 점이다. 실제 이상치는 예상치 못한곳에서 발생한다.
• 이러한 문제를 해결하기 위해서 Weakly supervised AD(혹은 open-set supervised AD) 를 만들었다. ****
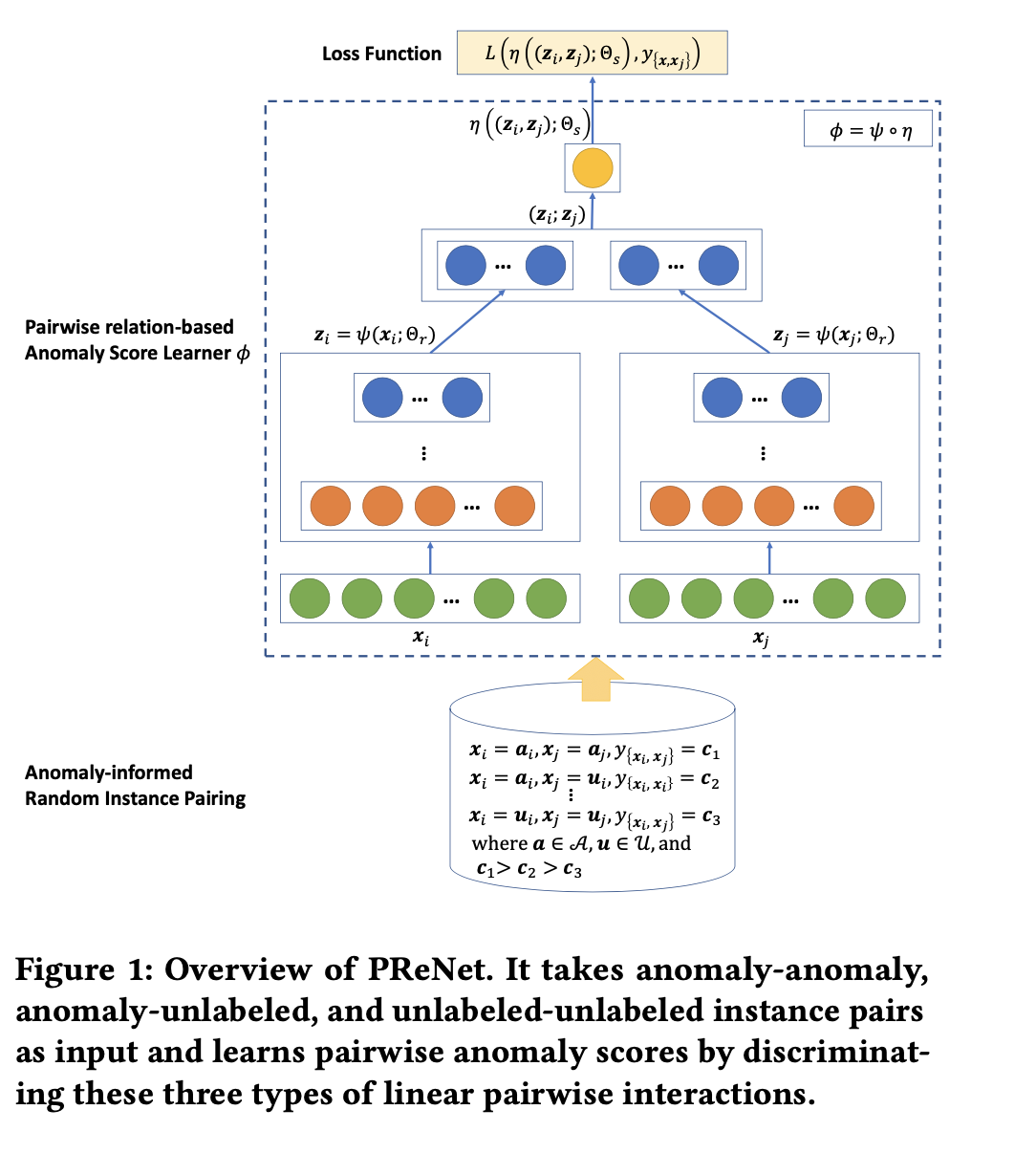
• 새로운 AD 모델인 Pairwise Relation PredictionNetwork(RPeNet)을 소개한다. 이 모델은 관련된 특성의 데이터를 한 쌍으로 묶어서 비교하며 학습하는 모델이다. 두 데이터의 관계 예측과 anomaly scoring으로 접근한다.

The Proposed Apporoach

1. overview of our approach PReNet

2. The Instantiated Model
   

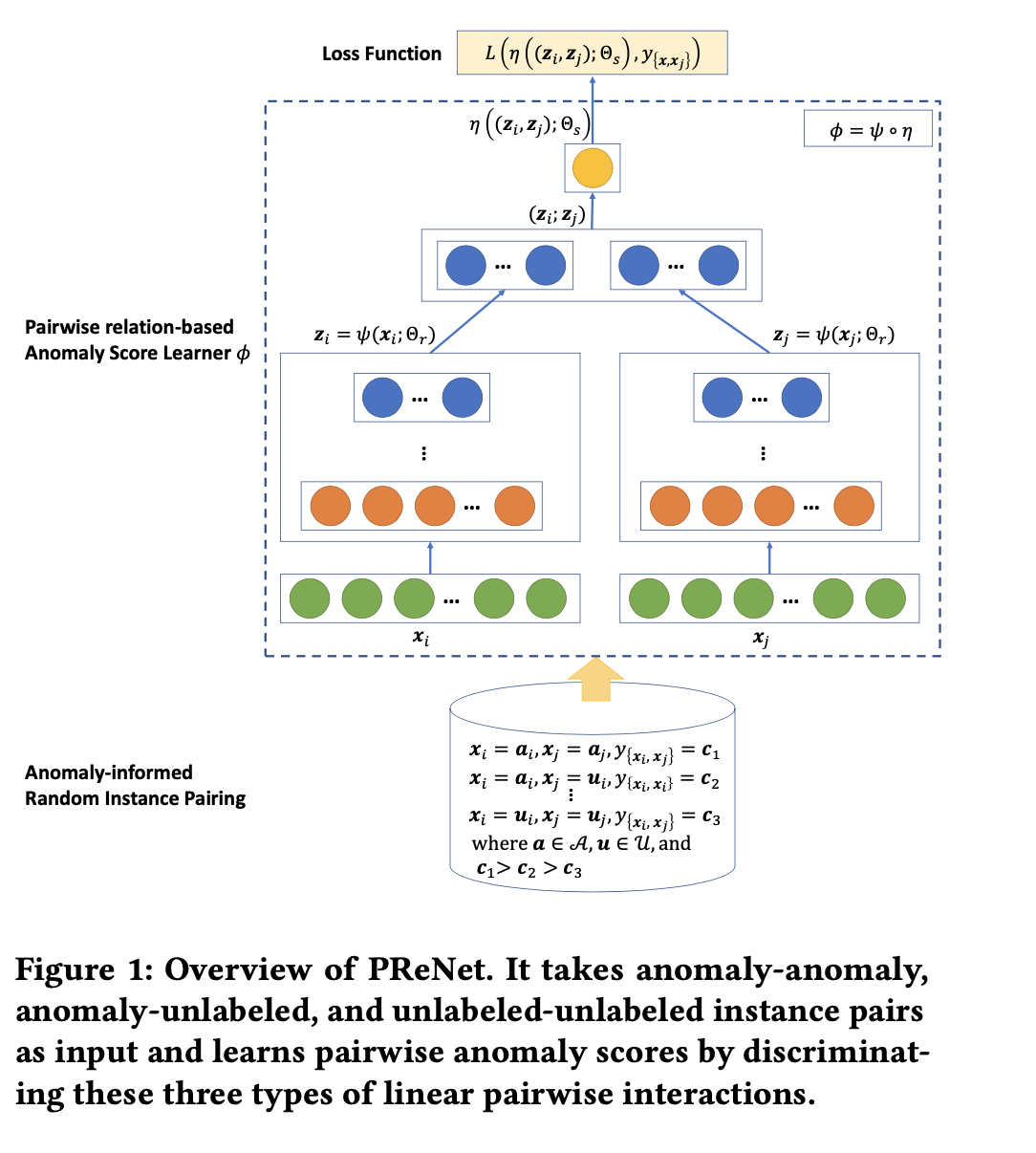
• $x_i, x_j$에는 anomaly와 unlabeled 가 섞여있다.
• $\psi$는 feature learner, $\eta$는 anomaly score, $\phi$는 score function(=anomaly score)

• feature와 anomaly score를 계산할 때, fully connected layer를 사용한다.

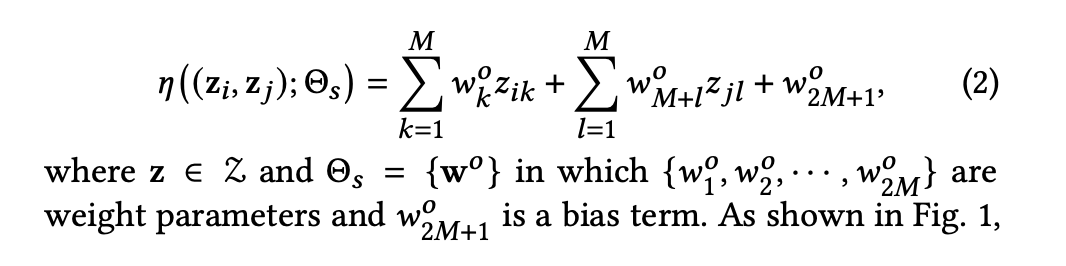
• z에 붙은 k와 l은 $z_i, z_j$set 안에 있는 index를 말한다.

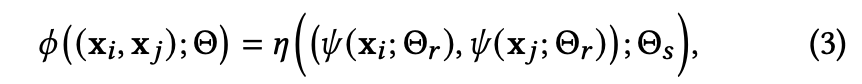
• 풀어쓰면 아래와 같다

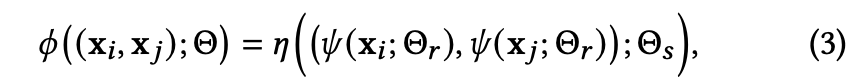
최종적인 loss function은 아래와 같다

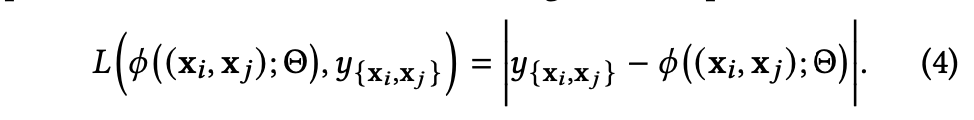
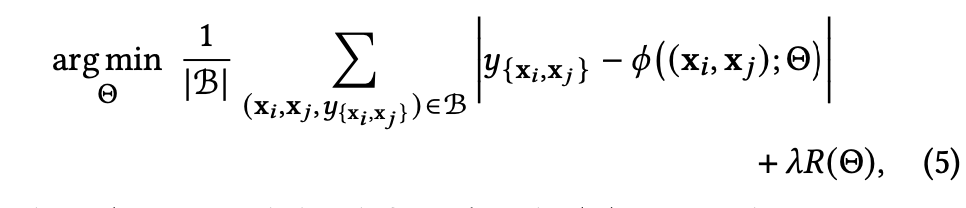
결론은 feature를 fc layer로 학습하는데 dataset을 pair로 구성해서 augmentation 효과를 내어 성능을 향상시켰다.

Loss fuction

Theoretical Analysis

1. Robust Anomaly Score Learning

   PReNet 모델을 unlabeled data를 normal data로 가정하고 학습을 한다. 하지만 unlabeled data에서 normal이 아닌 abnormal data가 존재한다면 학습에 문제가 되진 않을까? 결론부터 말하자면 거의 영향이 없다. 현실 세계에서 abnormal data는 아주 소수만 존재한다.
   
   위 표에 따르면 $\epsilon$은 unlabeled data에서 abnormal data가 존재할 확률이다. 전부 합했을때 $2\epsilon - \epsilon^2$만큼의 노이즈 확률이 존재한다. 이는 현실에서 $\epsilon$ ≤2.5% 정도의 abnormal data가 나오는 것으로 볼때 얼마 되지 않는 값이다. 따라서 unlabeled data에 존재할지 모르는 abnormal data는 학습에 큰 문제가 되지 않는다.

Experiment

1. Datasets
   • seen anomaly detection datasets
   • unseen anomaly detection datasets
2. Performance Evaluation metric
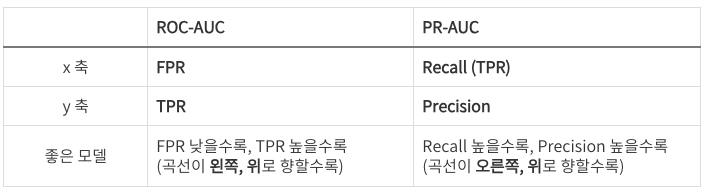
   • the Area Under Receiver Operating Characteristic Curve(AUC-ROC)
   • Area Under Precision-Recall Curve(AUC-PR)

- we have $\epsilon < \frac{2}{3}$ for our default setting: 𝑐1 = 8, 𝑐2 = 4 and 𝑐3 = 0

3. result
   

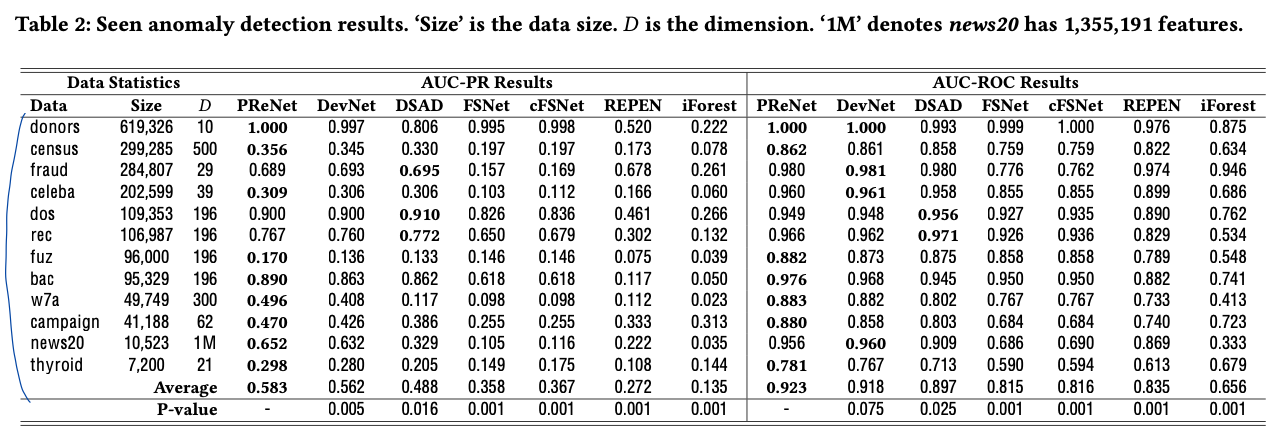
3. RESULT

• augmentation 방법으로 적절할 것으로 보인다.
• time series data에는 완전 적합하진 않아보인다. 하지만 feature learning 부분을 lstm과 같은 시계열 모델을 사용한다면 가능 할 수 있을 것 같다.

4. ADDITION

Code

x

Additional Materiar

• Deep Weakly-supervised Anomaly Detection

joint training, alternate training

ROC(Receiver Operating Characteristic) curve 와 AUC(Area Under the Curve)

ROC-AUC, PR-AUC 개념 비교 정리