hands-on 서적을 참고한 글입니다.
목표
사이킷런 (scikit-learn)을 사용하지 않고softmax로 붓꽃 분류를 해보자.
(데이터셋 임포트를 위한 sklearn 사용은 제외)
1. import
import numpy as np
from sklearn import datasets
iris = datasets.load_iris()
list(iris.keys())
X = iris["data"][:, (2,3)] # length, width
y = iris["target"]X_with_bias = np.c_[np.ones([len(X),1]), X]- 편향 특성을 추가한다. (1로 초기화)
np.random.seed(2042)2. train & test split
- sklearn의
train_test_split기능을 구현한다.
test_ratio = 0.2
validation_ratio = 0.2
total_size = len(X_with_bias)
test_size = int(total_size * test_ratio)
validation_size = int(total_size * validation_ratio)
train_size = total_size - test_size - validation_size
rnd_indices = np.random.permutation(total_size)
X_train = X_with_bias[rnd_indices[:train_size]]
y_train = y[rnd_indices[:train_size]]
X_valid = X_with_bias[rnd_indices[train_size:-test_size]]
y_valid = y[rnd_indices[train_size:-test_size]]
X_test = X_with_bias[rnd_indices[-test_size:]]
y_test = y[rnd_indices[-test_size:]]3. one hot encoding
- sklearn의
OneHotEncoder기능을 구현한다.
def to_one_hot(y):
n_classes = y.max() + 1
m = len(y)
Y_one_hot = np.zeros((m, n_classes))
Y_one_hot[np.arange(m), y] = 1
return Y_one_hoty_train[:10]
to_one_hot(y_train[:10])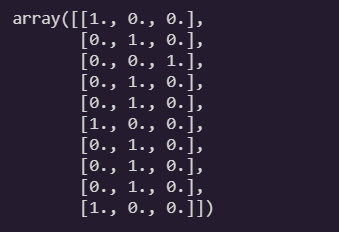
Y_train_one_hot = to_one_hot(y_train)
Y_valid_one_hot = to_one_hot(y_valid)
Y_test_one_hot = to_one_hot(y_test)4. softmax
def softmax(logits):
exps = np.exp(logits)
exp_sums = np.sum(exps, axis=1, keepdims=True)
return exps / exp_sumsn_inputs = X_train.shape[1] # 2 features and bias ( == 3 )
n_outputs = len(np.unique(y_train)) # 3 iris classes ( == 3)Cost function
Gradient function
eta = 0.01
n_iterations = 5001
m = len(X_train)
epsilon = 1e-7 # avoid nan (ex. log(0))
theta = np.random.randn(n_inputs, n_outputs)
for iteration in range(n_iterations):
logits = X_train.dot(theta) # softmax score
Y_proba = softmax(logits)
if iteration % 500 == 0:
loss = -np.mean(np.sum(Y_train_one_hot * np.log(Y_proba + epsilon), axis=1))
print(iteration, loss)
error = Y_proba - Y_train_one_hot
gradients = 1/m * X_train.T.dot(error)
theta = theta - eta * gradients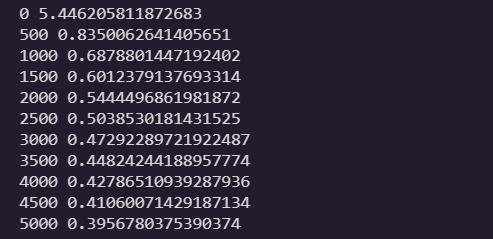
theta
logits = X_valid.dot(theta)
y_proba = softmax(logits)
y_predict = np.argmax(y_proba, axis=1)
accuracy_score = np.mean(y_predict == y_valid)
accuracy_score
5. early stopping
eta = 0.1
n_iterations = 5001
m = len(X_train)
epsilon = 1e-7
alpha = 0.1
best_loss = np.infty
theta = np.random.randn(n_inputs, n_outputs)
for iteration in range(n_iterations):
logits = X_train.dot(theta)
Y_proba = softmax(logits)
error = Y_proba - Y_train_one_hot
gradients = 1/m * X_train.T.dot(error) + np.r_[np.zeros([1, n_outputs]), alpha * theta[1:]]
theta = theta - eta * gradients
# caculate loss using validation set
logits = X_valid.dot(theta)
Y_proba = softmax(logits)
xentropy_loss = -np.mean(np.sum(Y_valid_one_hot * np.log(Y_proba + epsilon), axis=1))
l2_loss = 1/2 * np.sum(np.square(theta[1:])) # Ridge regularization
loss = xentropy_loss + alpha * l2_loss
if iteration % 500 == 0:
print(iteration, loss)
if loss < best_loss:
best_loss = loss
else:
print(iteration - 1, best_loss)
print(iteration, loss, "early stopped")
break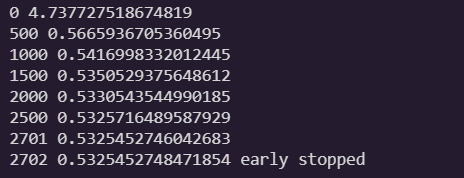
logits = X_valid.dot(theta)
Y_proba = softmax(logits)
y_predict = np.argmax(Y_proba, axis=1)
accuracy_score = np.mean(y_predict == y_valid)
accuracy_score
x0, x1 = np.meshgrid(
np.linspace(0, 8, 500).reshape(-1, 1),
np.linspace(0, 3.5, 200).reshape(-1, 1)
)
X_new = np.c_[x0.ravel(), x1.ravel()]
X_new_with_bias = np.c_[np.ones([len(X_new), 1]), X_new]
logits = X_new_with_bias.dot(theta)
Y_proba = softmax(logits)
y_predict = np.argmax(Y_proba, axis=1)
zz1 = Y_proba[:, 1].reshape(x0.shape)
zz = y_predict.reshape(x0.shape)
import matplotlib.pyplot as plt
plt.figure(figsize=(10, 4))
plt.plot(X[y==2, 0], X[y==2, 1], "g^", label="Iris virginica")
plt.plot(X[y==1, 0], X[y==1, 1], "bs", label="Iris versicolor")
plt.plot(X[y==0, 0], X[y==0, 1], "yo", label="Iris setosa")
from matplotlib.colors import ListedColormap
custom_cmap = ListedColormap(['#fafab0','#9898ff','#a0faa0'])
plt.contourf(x0, x1, zz, cmap=custom_cmap)
contour = plt.contour(x0, x1, zz1, cmap=plt.cm.brg)
plt.clabel(contour, inline=1, fontsize=12)
plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14)
plt.legend(loc="upper left", fontsize=14)
plt.axis([0, 7, 0, 3.5])
plt.show()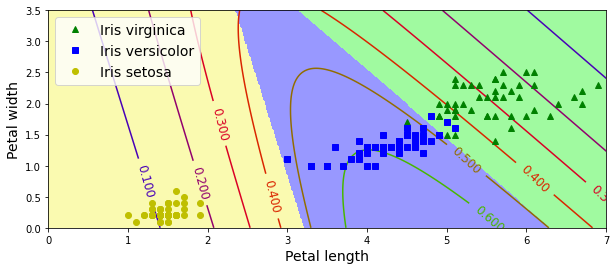
logits = X_test.dot(theta)
Y_proba = softmax(logits)
y_predict = np.argmax(Y_proba, axis=1)
accuracy_score = np.mean(y_predict == y_test)
accuracy_score

