스터디노트 (DeepLearning 2)

Deep Learning from scratch

Deep Learning from scratch - 순방향연산 및 간단한 학습원리

• chapter 42
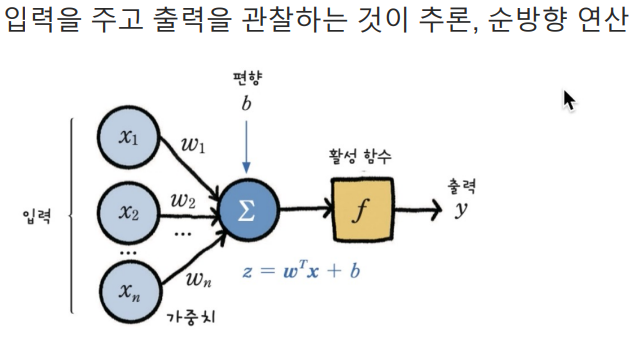
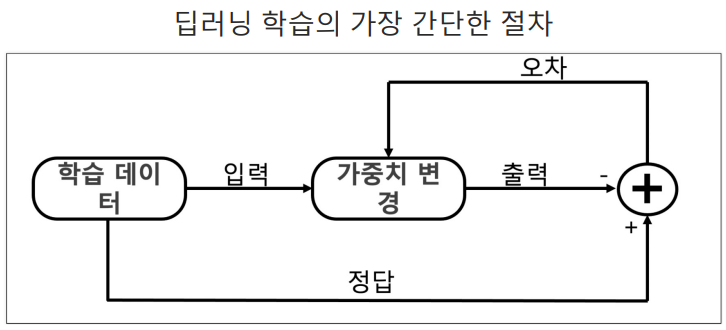
• 입력을 주고 출력을 관찰하는 것이 추론, 순방향 연산

# 데이터 준비

import numpy as np

X = np.array([
    [0, 0, 1], 
    [0, 1, 1], 
    [1, 0, 1], 
    [1, 1, 1]
])

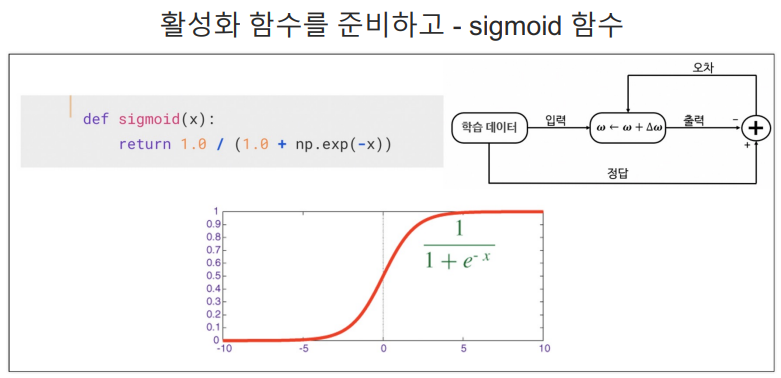
# 활성화 함수 준비 - sigmoid 함수

def sigmoid(x):
    return 1.0 / (1.0 + np.exp(-x))

# 가중치를 랜덤하게 선택
# 원래는 학습이 완료된 가중치를 사용해야 한다

W = 2*np.random.random((1, 3)) - 1
W

# 추론 결과

N = 4
for k in range(N):
    x = X[k, :].T
    v = np.matmul(W, x)
    y  = sigmoid(v)
    
    print(v)

• 가중치가 이제 정답을 맞추도록 학습을 시켜야 한다

# 정답을 주자 - AND

import numpy as np

#X = np.array([[0, 0, 1], [0, 1, 1], [1, 0, 1], [1, 1, 1]])

D = np.array([[0], [0], [1], [1]])

# 모델의 출력을 계산하는 함수

def calc_output(W,x):
    v = np.matmul(W, x)
    y = sigmoid(v)
    
    return y

# 오차 계산

def calc_error(d, y): # d : 정답, y : 추론값
    e = d - y
    delta = y*(1-y)*e 
    
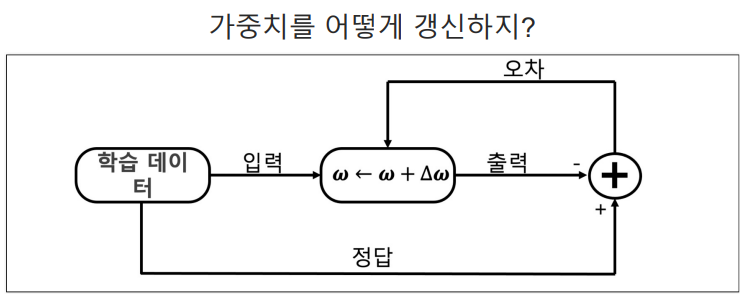
    return delta

# 한 epoch에 수행되는 W의 계산

def delta_GD(W, X, D, alpha):
    for k in range(4):
        x = X[k, :].T
        d = D[k]
        
        y = calc_output(W, x)
        delta = calc_error(d, y)
        
        dW = alpha*delta*x # alpha : 학습률
        W = W + dW
        
    return W

# 가중치를 랜덤하게 초기화하고 학습 시작

W = 2*np.random.random((1, 3)) -1

# 가중치는 업데이트가 된다
alpha = 0.9
for epoch in range(10000):
    W = delta_GD(W, X, D, alpha)
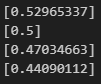
    print(W)

# 결과 확인

N = 4

for k in range(N):
    x = X[k, :].T
    v = np.matmul(W, x)
    y = sigmoid(v)
    print(y)

W

X

D

---

Deep Learning from scratch - 오차의 역전파(XOR)

# XOR 데이터

import numpy as np

X = np.array([[0, 0, 1], 
              [0, 1, 1], 
              [1, 0, 1], 
              [1, 1, 1]])

D = np.array([[0], [1], [1], [0]])

W = 2*np.random.random((1, 3)) - 1

# 활성화 함수 준비 - sigmoid 함수

def sigmoid(x):
    return 1.0 / (1.0 + np.exp(-x))

# 모델의 출력을 계산하는 함수

def calc_output(W,x):
    v = np.matmul(W, x)
    y = sigmoid(v)
    
    return y

# 오차 계산

def calc_error(d, y): # d : 정답, y : 추론값
    e = d - y
    delta = y*(1-y)*e 
    
    return delta

# 한 epoch에 수행되는 W의 계산

def delta_GD(W, X, D, alpha):
    for k in range(4):
        x = X[k, :].T
        d = D[k]
        
        y = calc_output(W, x)
        delta = calc_error(d, y)
        
        dW = alpha*delta*x # alpha : 학습률
        W = W + dW
        
    return W

# 학습 train

alpha = 0.9
for epoch in range(10000): 
    W = delta_GD(W, X, D, alpha)

# 결과 확인 - 엉망

N = 4
for k in range(N):
    x = X[k, :].T
    v = np.matmul(W, x)
    y = sigmoid(v)
    print(y)
    

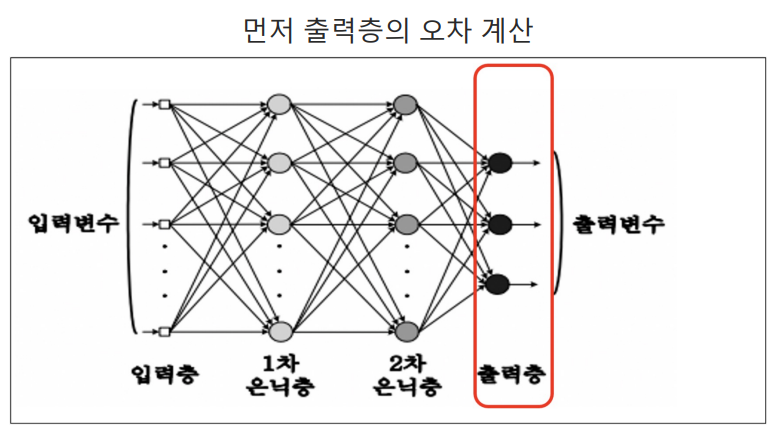
• 역전파
  - 단층의 경우, 정답과 출력의 오차를 계산해서 가중치를 갱신할 수 있다.
  - 다층 신경망은 그럴 수 없다.
  - Backpropagation 개념 개발됨

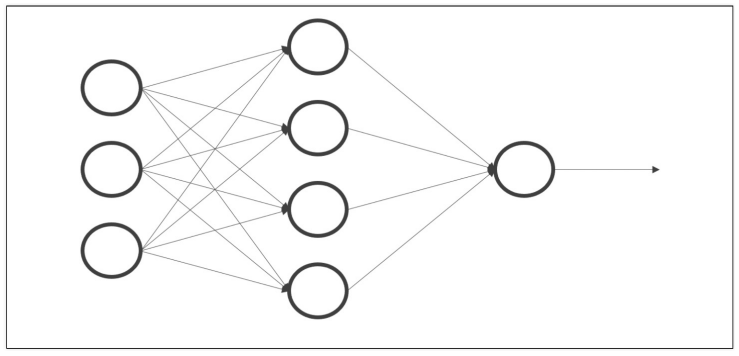
• 다시 새로운 구조

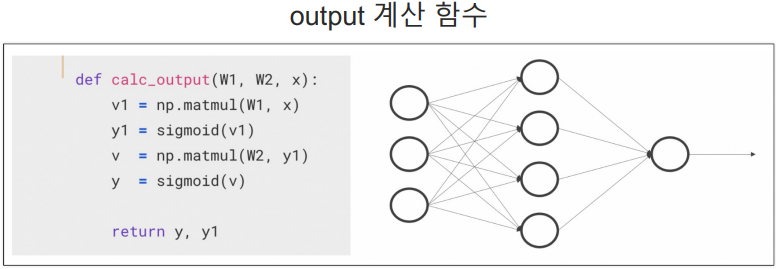
# output 계산 함수 
# W1, W2는 layer 사이의 가중치(?..)

def calc_output(W1, W2, x):
    v1 = np.matmul(W1, x)
    y1 = sigmoid(v1)
    v = np.matmul(W2, y1)
    y = sigmoid(v)
    
    return y, y1

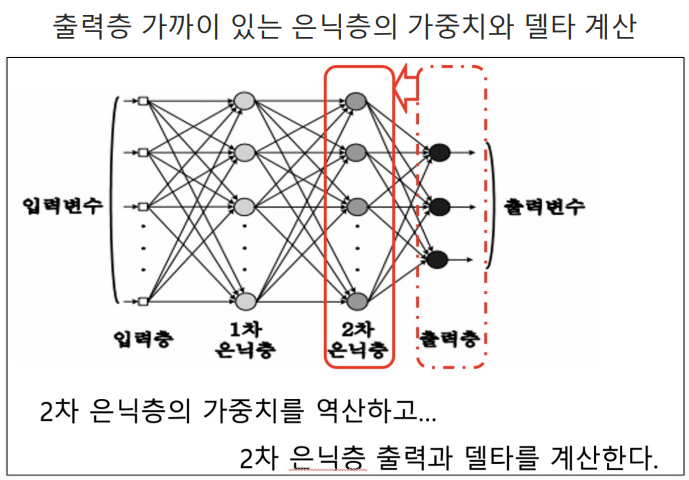
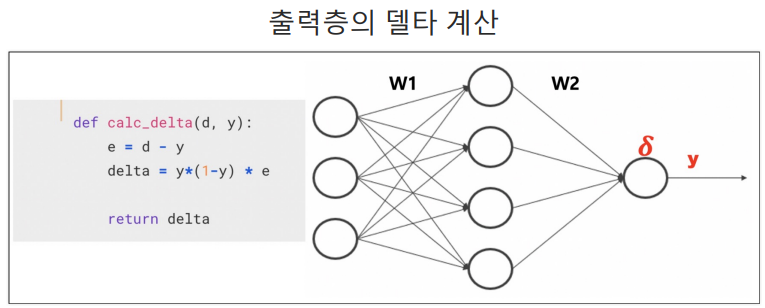
# 출력층의 델타 계산

def calc_delta(d, y):
    e = d - y
    delta = y*(1-y)*e
    
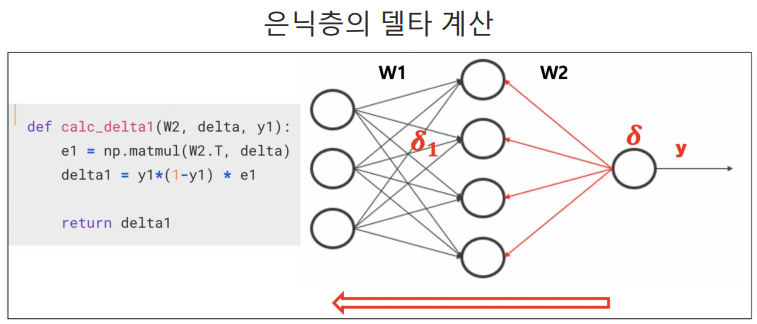
    return delta

# 은닉층의 델타 계산

def calc_delta1(W2, delta, y1):
    e1 = np.matmul(W2.T, delta)
    delta1 = y1*(1-y1)*e1
    
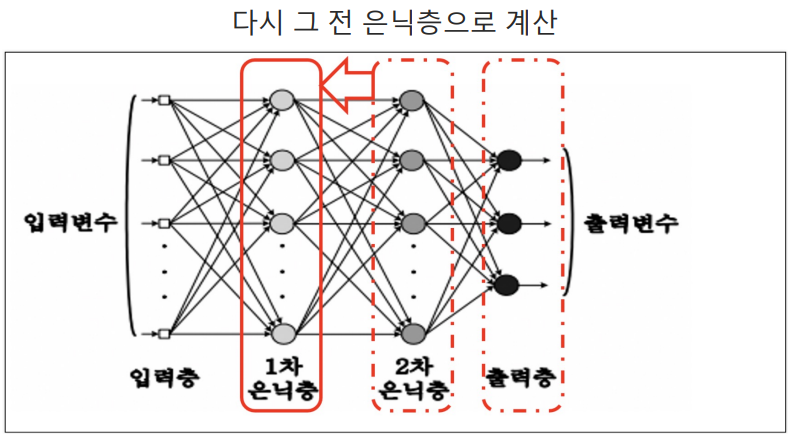
    return delta1

• 역전파 코드

# 역전파 코드

def backprop_XOR(W1, W2, X, D, alpha):
    for k in range(4):
        x = X[k, :].T
        d = D[k]
        
        y, y1 = calc_output(W1, W2, x)
        delta = calc_delta(d, y)
        delta1 = calc_delta1(W2, delta, y1)
        
        dW1 = (alpha*delta1).reshape(4, 1)*x.reshape(1, 3)
        W1 = W1 + dW1
        
        dW2 = alpha * delta * y1
        W2 = W2 + dW2
    
    return W1, W2

# 데이터를 준비하고 가중치를 랜덤하게 초기화

X = np.array([[0, 0, 1], [0, 1, 1], [1, 0, 1], [1, 1, 1]])
D = np.array([[0], [1], [1], [0]])

W1 = 2*np.random.random((4, 3)) -1
W2 = 2*np.random.random((1, 4)) -1

# 학습

alpha = 0.9

for epoch in range(10000):
    W1, W2 = backprop_XOR(W1,W2, X, D, alpha)

# 결과

N = 4
for k in range(4):
    x = X[k, :].T
    v1 = np.matmul(W1, x)
    y1 = sigmoid(v1)
    v = np.matmul(W2, y1)
    y = sigmoid(v)
    print(y)

---

Deep Learning from scratch - 크로스엔트로피(Loss)

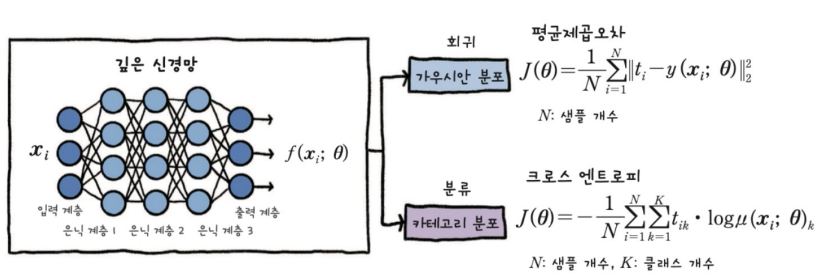
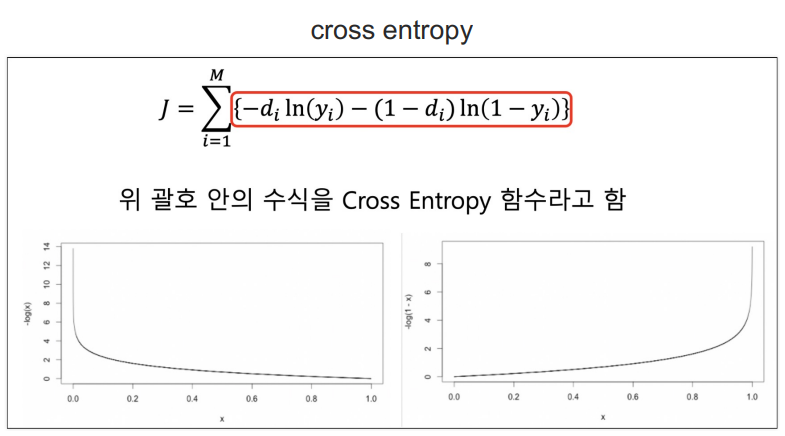
• 델타를 구할 때 Cross Entropy 함수를 사용하면 델타는 오차와 같다

# 활성화 함수 준비 - sigmoid 함수
import numpy as np


def sigmoid(x):
    return 1.0 / (1.0 + np.exp(-x))

# output 계산 함수 
# W1, W2는 layer 사이의 가중치(?..)

def calc_output(W1, W2, x):
    v1 = np.matmul(W1, x)
    y1 = sigmoid(v1)
    v = np.matmul(W2, y1)
    y = sigmoid(v)
    
    return y, y1

# cross_entropy의 델타

def calcDelta_ce(d, y):
    e = d - y
    delta = e
    
    return delta

# 은닉층에서

def calcDelta1_ce(W2, delta, y1):
    e1 = np.matmul(W2.T, delta)
    delta1 = y1*(1-y1)*e1
    
    return delta1

# 다시 역전파

def BackpropCE(W1, W2, X, D, alpha):
    for k in range(4):
        x = X[k, :].T
        d = D[k]
        
        y, y1 = calc_output(W1, W2, x)
        delta = calcDelta_ce(d, y)
        delta1 = calcDelta1_ce(W2, delta, y1)
        
        dW1 = (alpha*delta1).reshape(4, 1) * x.reshape(1, 3)
        W1 = W1 + dW1
        
        dW2 = alpha * delta * y1
        W2 = W2 + dW2
        
        return W1, W2

# 학습

X = np.array([[0, 0, 1], [0, 1, 1], [1, 0, 1], [1, 1, 1]])
D = np.array([[0], [1], [1], [0]])

W1 = 2*np.random.random((4, 3)) -1
W2 = 2*np.random.random((1, 4)) -1

alpha = 0.9

for epoch in range(10000):
    W1, W2 = BackpropCE(W1, W2, X, D, alpha=0.9)

# 결과

N = 4

for k in range(N):
    x = X[k, :].T
    v1 = np.matmul(W1, x)
    y1 = sigmoid(v1)
    v = np.matmul(W2, y1)
    y = sigmoid(v)
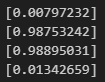
    print(y)

결과가 약간 이상하게 나온다..?...;;

💻 출처 : 제로베이스 데이터 취업 스쿨