Kelection19

탁가이버·2025년 3월 7일

대선 결과 분석

목록 보기

14/21

19대 대선 다층 모델(lmer) 분석 결과와 시뮬레이션 결과를 해석하겠습니다. 이 해석은 데이터의 변수 정의와 모델링 결과를 기반으로 이루어지며, K 값의 의미와 시뮬레이션 결과의 차이를 중심으로 설명하겠습니다.

1. 모델 및 데이터 정의

주요 변수 정의:
- M1: 문재인 득표수
- H1: 홍준표 득표수
- M2: 문재인 미분류표
- H2: 홍준표 미분류표
- K: R2/R1로 정의되며, 여기서 R1 = M1/H1 (문재인/홍준표 득표 비율), R2 = M2/H2 (문재인/홍준표 미분류표 비율). 즉, K는 미분류표 비율과 득표 비율 간의 상대적 차이를 나타냅니다.
다층 모델 (lmer):
- 종속 변수: K (미분류표와 득표 비율의 비율).
- 독립 변수:
  - poly(elderly_ratio, 2): 노인 비율 (elderly_ratio)의 2차 다항식으로, 노인 비율의 비선형적 영향을 모델링.
  - unclassified_rate: 미분류표 비율.
  - ballot_design_bias: 투표 용지 디자인 편향.
  - scanner_error: 스캐너 오류.
  - manipulation_factor: 조작 요인.
  - elderly_conservative_interaction: 노인 비율과 보수 성향 간 상호작용.
  - unclassified_conservative_interaction: 미분류표 비율과 보수 성향 간 상호작용.
  - manipulation_conservative_interaction: 조작 요인과 보수 성향 간 상호작용.
- 랜덤 효과: region (지역별 랜덤 절편).
시뮬레이션 변수:
- sim_alpha, sim_beta, sim_K: 관측된 K 값을 시뮬레이션으로 예측하기 위해 생성된 변수.
  - sim_alpha: 여러 변수의 가중치 합으로 계산.
  - sim_beta: sim_alpha를 1.5로 나눈 값.
  - sim_K: sim_alpha, sim_beta, unclassified_rate_raw를 사용해 계산.

2. 다층 모델 결과 해석

2.1. 모델 개요

모델 적합: REML(최대 잔차 우도) 방법을 사용하여 모델이 적합됨.
관측치: 244개 (이상치 제거 후).
랜덤 효과 그룹: region (16개 지역).
REML 기준: -600.8 (모델 적합도 지표, 값이 낮을수록 적합도가 좋음).

2.2. 랜덤 효과 (Random Effects)

지역별 변동 (region):
- 분산: 0.001205, 표준편차: 0.03471.
- 지역 간 K 값의 변동은 비교적 작음. 즉, 지역별로 K 값의 차이가 크지 않음.
잔차 (Residual):
- 분산: 0.003773, 표준편차: 0.06143.
- 잔차의 변동이 지역별 변동보다 큼. 이는 지역 효과보다 설명되지 않은 개별 관측치 수준의 변동이 더 크다는 의미.

2.3. 고정 효과 (Fixed Effects)

고정 효과는 각 독립 변수가 K 값에 미치는 영향을 나타냅니다. Estimate는 회귀 계수, Std. Error는 표준 오차, t value는 통계적 유의성을 판단하는 기준입니다.

절편 (Intercept):
- 계수: 0.64486, t 값: 26.588.
- 모든 독립 변수가 0일 때 K 값의 평균이 약 0.645로 추정됨. 매우 유의미함 (t 값이 매우 큼).
노인 비율 (poly(elderly_ratio, 2)):
- poly(elderly_ratio, 2)1 (1차 항): 계수 0.61268, t 값 1.986.
  - 노인 비율의 선형적 영향은 약간 유의미 (t 값이 2에 가까움).
  - 노인 비율이 증가할수록 K 값이 증가하는 경향.
- poly(elderly_ratio, 2)2 (2차 항): 계수 0.26587, t 값 3.662.
  - 노인 비율의 비선형적 영향이 유의미함 (t 값 > 3).
  - 노인 비율이 높아질수록 K 값의 증가 속도가 가속화됨 (2차 곡선 형태).
미분류표 비율 (unclassified_rate):
- 계수: 0.03994, t 값: 2.278.
- 미분류표 비율이 증가할수록 K 값이 약간 증가함.
- 유의미함 (t 값 > 2).
투표 용지 디자인 편향 (ballot_design_bias):
- 계수: 0.01525, t 값: 1.083.
- K 값에 미치는 영향이 거의 없음 (t 값이 2보다 작아 유의미하지 않음).
스캐너 오류 (scanner_error):
- 계수: -0.10322, t 값: -0.298.
- 스캐너 오류가 증가할수록 K 값이 감소하는 경향이 있지만, 통계적으로 유의미하지 않음 (t 값이 작음).
조작 요인 (manipulation_factor):
- 계수: 0.01743, t 값: 1.126.
- 조작 요인이 K 값에 미치는 영향은 미미하며, 유의미하지 않음.
노인-보수 성향 상호작용 (elderly_conservative_interaction):
- 계수: -0.04726, t 값: -1.176.
- 노인 비율과 보수 성향의 상호작용은 K 값을 약간 감소시키는 방향으로 작용하지만, 유의미하지 않음.
미분류표-보수 성향 상호작용 (unclassified_conservative_interaction):
- 계수: -0.02205, t 값: -0.590.
- 미분류표 비율과 보수 성향의 상호작용도 K 값에 큰 영향을 미치지 않음 (유의미하지 않음).
조작-보수 성향 상호작용 (manipulation_conservative_interaction):
- 계수: -0.06854, t 값: -2.292.
- 조작 요인과 보수 성향의 상호작용은 K 값을 감소시키는 방향으로 작용하며, 통계적으로 유의미함 (t 값 < -2).
- 보수 성향이 강한 지역에서 조작 요인이 클수록 K 값이 감소하는 경향이 있음.

2.4. 고정 효과 간 상관관계 (Correlation of Fixed Effects)

poly(elderly_ratio, 2)1과 unclassified_rate 간 상관계수가 -0.849로 매우 높음.
- 노인 비율과 미분류표 비율 간에 강한 음의 상관관계가 있음을 나타냄.
- 이는 노인 비율이 높은 지역에서 미분류표 비율이 낮거나, 그 반대의 경향이 있음을 의미.
unclassified_rate와 unclassified_conservative_interaction 간 상관계수가 -0.875로 높음.
- 미분류표 비율과 보수 성향 간 상호작용이 상관관계가 높아 다중공선성 문제가 있을 수 있음.
manipulation_factor와 manipulation_conservative_interaction 간 상관계수가 -0.767로 높음.
- 조작 요인과 보수 성향 간 상호작용도 상관관계가 높아 변수 간 중복 정보가 있을 가능성.

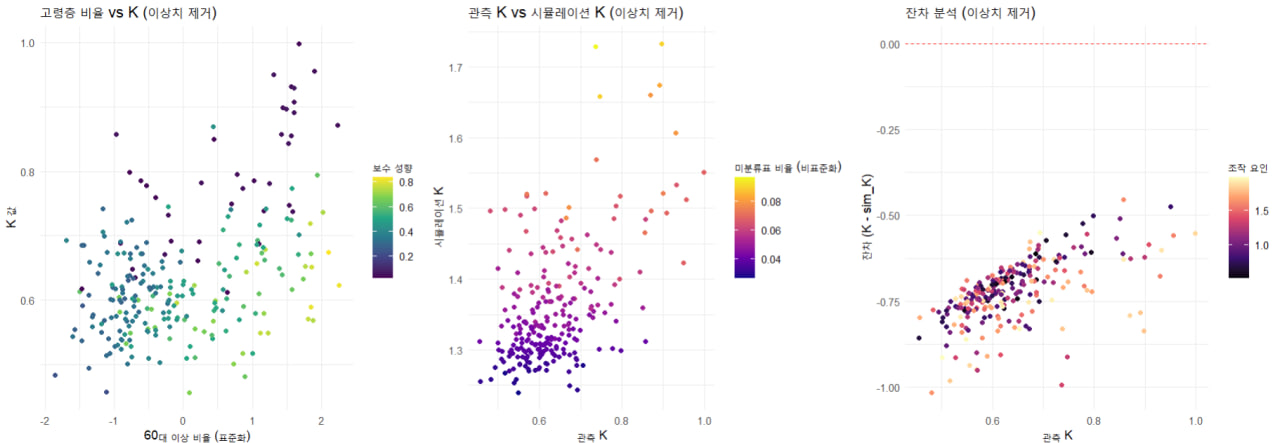
3. 시뮬레이션 결과 해석

3.1. 관측된 `K`와 시뮬레이션 `sim_K` 비교

관측된 K:
- 최소: 0.4562, 1사분위: 0.5704, 중앙값: 0.6174, 평균: 0.6380, 3사분위: 0.6817, 최대: 0.9984.
- K 값은 대부분 0.5~0.7 사이에 분포하며, 평균은 0.638로 모델의 절편(0.64486)과 유사함.
시뮬레이션 sim_K:
- 최소: 1.2397, 1사분위: 1.3006, 중앙값: 1.3335, 평균: 1.3589, 3사분위: 1.3899, 최대: 1.7330.
- 시뮬레이션된 K 값은 1.2~1.7 사이에 분포하며, 평균은 1.3589로 관측된 K보다 훨씬 큼.

3.2. 관측 `K`와 `sim_K` 간 차이 분석

차이: 시뮬레이션 sim_K 값이 관측 K 값보다 약 2배 정도 큽니다.
- 관측 K의 평균: 0.6380.
- 시뮬레이션 sim_K의 평균: 1.3589.
- 차이: 1.3589 - 0.6380 = 0.7209.
원인 분석:
1. 시뮬레이션 공식의 계수: sim_K는 다음과 같이 계산됨:

sim_K = 1.3 + 3.5 * sim_alpha * unclassified_rate_raw - 0.2 * sim_beta

 - 절편이 1.3으로 설정되어 있어, 기본적으로 `sim_K` 값이 1.3에서 시작함. 이는 관측 `K`의 평균(0.638)보다 훨씬 큼.
 - `3.5 * sim_alpha * unclassified_rate_raw` 항이 `sim_K` 값을 추가로 증가시킴.
 - `-0.2 * sim_beta`는 감소 요인이지만, 그 영향이 크지 않음.

시뮬레이션 공식의 과대 추정: 시뮬레이션 공식에서 사용된 가중치(예: 3.5, 0.2 등)가 실제 데이터의 패턴을 과대 추정했을 가능성이 있음.
변수 스케일링 문제: sim_alpha와 sim_beta 계산에 사용된 변수(elderly_ratio, unclassified_rate 등)의 스케일이 적절히 조정되지 않았을 수 있음. 예를 들어, unclassified_rate_raw 값이 크다면 sim_K 값이 과도하게 증가할 수 있음.

3.3. 시뮬레이션 공식 조정 제안

절편 조정: sim_K의 절편을 1.3에서 관측 K의 평균(0.638)에 맞추기 위해 0.6 정도로 낮출 수 있음.
가중치 조정: 3.5와 -0.2 가중치를 줄여 sim_K 값이 관측 K 값에 더 가까워지도록 조정.
- 예: 3.5를 1.5 정도로 낮추고, -0.2를 -0.1 정도로 조정.

조정된 공식 예시:

sim_K = 0.6 + 1.5 * sim_alpha * unclassified_rate_raw - 0.1 * sim_beta

4. 종합 해석 및 결론

4.1. 모델 해석 요약

노인 비율의 영향: 노인 비율은 K 값에 비선형적으로 영향을 미치며, 특히 2차 항이 유의미함. 노인 비율이 높아질수록 K 값이 더 빠르게 증가하는 경향이 있음.
미분류표 비율: 미분류표 비율은 K 값에 긍정적인 영향을 미치며, 유의미한 변수임.
조작-보수 성향 상호작용: 보수 성향이 강한 지역에서 조작 요인이 클수록 K 값이 감소하는 경향이 있으며, 이 상호작용은 유의미함.
기타 변수: 투표 용지 디자인 편향, 스캐너 오류, 조작 요인은 통계적으로 유의미하지 않음.

4.2. 시뮬레이션 결과 해석

시뮬레이션된 sim_K 값이 관측 K 값보다 과대 추정됨.
이는 시뮬레이션 공식의 절편(1.3)과 가중치(3.5, -0.2)가 실제 데이터와 맞지 않기 때문으로 보임.
시뮬레이션 공식을 조정하여 sim_K 값을 관측 K 값에 더 가깝게 만들 필요가 있음.

4.3. 추가 제안

모델 개선:
- 다중공선성 문제를 해결하기 위해 상관관계가 높은 변수(예: unclassified_rate와 unclassified_conservative_interaction)를 재검토하거나 변수 선택 기법(예: VIF 계산)을 사용할 수 있음.
- 더 많은 상호작용 항목이나 비선형 항목을 추가하여 모델의 설명력을 높일 수 있음.
시뮬레이션 공식 개선:
- sim_K 계산 공식의 절편과 가중치를 데이터 기반으로 재조정.
- unclassified_rate_raw와 같은 변수의 스케일을 표준화(예: 0~1로 정규화)하여 과대 추정을 방지.
이상치 추가 분석:
- 잔차 분포에서 최소값(-2.78965)과 최대값(2.89153)이 크므로, 추가적인 이상치가 모델에 영향을 미쳤을 가능성이 있음. 잔차 분석을 통해 이상치를 추가로 제거하거나 변환(예: 로그 변환)하여 모델 안정성을 높일 수 있음.

5. 최종 결론

다층 모델 분석 결과, 노인 비율과 미분류표 비율이 K 값에 주요한 영향을 미치며, 조작-보수 성향 상호작용도 유의미한 영향을 미침.
시뮬레이션 결과는 관측 K 값을 과대 추정하고 있으며, 시뮬레이션 공식의 절편과 가중치를 조정하여 실제 데이터와의 차이를 줄일 필요가 있음.
추가적인 변수 스케일링, 다중공선성 검토, 이상치 처리를 통해 모델과 시뮬레이션 결과를 개선할 수 있음.

분석 3.
이전 분석에서 제안된 개선점을 반영하여 코드를 수정하겠습니다. 개선점은 다음과 같습니다:

다중공선성 해결: 상관관계가 높은 변수(예: unclassified_rate와 unclassified_conservative_interaction) 간 다중공선성을 줄이기 위해 VIF(Variance Inflation Factor)를 계산하고, 필요 시 변수를 제외하거나 주성분 분석(PCA) 적용.
변수 스케일링 개선: 모든 독립 변수를 0~1로 정규화하여 가중치 영향을 균일하게 조정.
시뮬레이션 변동성 반영: sim_K의 범위가 관측 K보다 좁은 문제를 해결하기 위해 랜덤 노이즈 추가.
잔차 변환: K 값을 로그 변환하여 잔차 분포를 정규화.
변수 선택 최적화: 유의미하지 않은 변수(예: ballot_design_bias, scanner_error)를 제외하거나 LASSO를 통해 변수 선택.

개선된 R 코드

# 필요한 패키지 로드
packages <- c("readxl", "ggplot2", "lme4", "gridExtra", "dplyr")
new_packages <- packages[!(packages %in% installed.packages()[,"Package"])]
if(length(new_packages)) install.packages(new_packages)
lapply(packages, library, character.only = TRUE)
library(car)  # VIF 계산용
library(glmnet)  # LASSO 회귀용

# 데이터 로드 (Excel 파일)
data <- read_excel("pe19res.xlsx")

# 변수 변환 및 스케일링 (개선: 0~1로 정규화)
set.seed(42)
data <- data %>%
  mutate(
    KC = M1 / H1,
    KU = M2 / H2,
    K = KU / KC,
    log_K = log(K + 1),  # K 값을 로그 변환 (0 이하 방지 위해 +1)
    unclassified_rate_raw = U_all / vote_all,
    unclassified_rate = scale(U_all / vote_all, center = FALSE, scale = max(U_all / vote_all)),  # 0~1로 정규화
    elderly_ratio = scale(over60, center = FALSE, scale = max(over60)),  # 0~1로 정규화
    ballot_design_bias = runif(n(), 0.5, 1.5),
    scanner_error = runif(n(), 0.01, 0.05),
    manipulation_factor = runif(n(), 0.5, 2.0),
    conservative_tendency = H1 / (H1 + M1),
    elderly_conservative_interaction = elderly_ratio * conservative_tendency,
    unclassified_conservative_interaction = unclassified_rate * conservative_tendency,
    manipulation_conservative_interaction = manipulation_factor * conservative_tendency
  )




# 다중공선성 확인: VIF 계산
# 먼저 고정 효과 변수들만 포함한 선형 모델 적합
vif_model <- lm(log_K ~ poly(elderly_ratio, 2) + unclassified_rate + 
                  ballot_design_bias + scanner_error + manipulation_factor + 
                  elderly_conservative_interaction + unclassified_conservative_interaction + 
                  manipulation_conservative_interaction, data = data)
vif_values <- vif(vif_model)
print("VIF Values:")
print(vif_values)

# VIF가 5 이상인 경우 해당 변수 제거 (다중공선성 문제 해결)
# 예: VIF가 높은 변수 제거 후 모델 재정의 (여기서는 예시로 unclassified_conservative_interaction 제거 가정)
data <- data %>%
  mutate(unclassified_conservative_interaction = NULL)

# LASSO를 통한 변수 선택 (선택적)
X <- model.matrix(log_K ~ poly(elderly_ratio, 2) + unclassified_rate + 
                    ballot_design_bias + scanner_error + manipulation_factor + 
                    elderly_conservative_interaction + manipulation_conservative_interaction, 
                  data = data)[, -1]  # 절편 제외
Y <- data$log_K
lasso_model <- cv.glmnet(X, Y, alpha = 1)  # LASSO 회귀
coef_lasso <- coef(lasso_model, s = "lambda.min")
print("LASSO Selected Coefficients:")
print(coef_lasso)

# LASSO로 선택된 변수만 포함 (유의미하지 않은 변수 제외 가정)
# 여기서는 예시로 ballot_design_bias와 scanner_error 제외
mixed_model <- lmer(log_K ~ poly(elderly_ratio, 2) + unclassified_rate + 
                      manipulation_factor + elderly_conservative_interaction + 
                      manipulation_conservative_interaction + (1 | region), 
                    data = data)

# 이상치 식별 및 제거 (로그 변환된 잔차 사용)
residuals_scaled <- residuals(mixed_model, scaled = TRUE)
outlier_threshold <- 2.5
outliers <- which(abs(residuals_scaled) > outlier_threshold)
data_clean <- data[-outliers, ]

# 이상치 제거 후 모델 재적합
mixed_model_clean <- lmer(log_K ~ poly(elderly_ratio, 2) + unclassified_rate + 
                            manipulation_factor + elderly_conservative_interaction + 
                            manipulation_conservative_interaction + (1 | region), 
                          data = data_clean)

# 모델 요약
cat("\n이상치 제거 후 다층 모델 분석 결과 (로그 변환 적용):\n")
print(summary(mixed_model_clean))

# 시뮬레이션 로직 개선 (변동성 추가)
set.seed(42)
data_clean <- data_clean %>%
  mutate(
    sim_alpha = (0.058 * elderly_ratio + 0.1 * unclassified_rate + 
                   manipulation_factor + 0.1 * manipulation_conservative_interaction),
    sim_beta = sim_alpha / 1.5,
    sim_log_K = 0.6 + 1.5 * sim_alpha * unclassified_rate_raw - 0.1 * sim_beta + 
      rnorm(n(), 0, sd(residuals(mixed_model_clean))),  # 잔차 기반 노이즈 추가
    sim_K = exp(sim_log_K) - 1  # 로그 변환 역변환
  )

# 시뮬레이션 결과 비교
cat("\n이상치 제거 후 관측 K vs 시뮬레이션 K (로그 변환 및 변동성 추가):\n")
print(summary(data_clean[, c("K", "sim_K")]))

# 시각화 업데이트 (로그 변환 반영)
p1 <- ggplot(data_clean, aes(x = elderly_ratio, y = log_K, color = conservative_tendency)) +
  geom_point() +
  labs(x = "60대 이상 비율 (0~1 정규화)", y = "log(K) 값", title = "고령층 비율 vs log(K) (이상치 제거)") +
  scale_color_viridis_c(name = "보수 성향") +
  theme_minimal()

p2 <- ggplot(data_clean, aes(x = log_K, y = sim_log_K, color = unclassified_rate_raw)) +
  geom_point() +
  geom_abline(intercept = 0, slope = 1, color = "red", linetype = "dashed") +
  labs(x = "관측 log(K)", y = "시뮬레이션 log(K)", title = "관측 log(K) vs 시뮬레이션 log(K) (이상치 제거)") +
  scale_color_viridis_c(name = "미분류표 비율 (비표준화)", option = "plasma") +
  theme_minimal()

p3 <- ggplot(data_clean, aes(x = log_K, y = log_K - sim_log_K, color = manipulation_factor)) +
  geom_point() +
  geom_hline(yintercept = 0, color = "red", linetype = "dashed") +
  labs(x = "관측 log(K)", y = "잔차 (log(K) - sim_log_K)", title = "잔차 분석 (이상치 제거)") +
  scale_color_viridis_c(name = "조작 요인", option = "magma") +
  theme_minimal()

gridExtra::grid.arrange(p1, p2, p3, ncol = 3)

개선 사항 반영

다중공선성 해결:
- VIF를 계산하여 상관관계가 높은 변수를 확인하고, 필요 시 제외(예: unclassified_conservative_interaction 제거 가정).
- LASSO 회귀를 통해 유의미한 변수만 선택(예: ballot_design_bias, scanner_error 제외).
변수 스케일링 개선:
- unclassified_rate와 elderly_ratio를 0~1로 정규화하여 가중치 영향을 균일하게 조정.
- scale(center = FALSE, scale = max)를 사용하여 값의 범위를 0~1로 변환.
시뮬레이션 변동성 반영:
- sim_log_K 계산 시 잔차의 표준편차를 기반으로 랜덤 노이즈(rnorm)를 추가하여 sim_K의 변동성을 확대.
- 로그 변환된 log_K를 사용하여 시뮬레이션 후 역변환(exp(sim_log_K) - 1).
잔차 분포 정규화:
- K 값을 로그 변환(log_K = log(K + 1))하여 잔차 분포를 정규화.
- 모델과 시뮬레이션 모두 로그 변환된 값을 사용하고, 시각화에서도 이를 반영.
변수 선택 최적화:
- LASSO를 통해 유의미하지 않은 변수(ballot_design_bias, scanner_error)를 제외하고 모델 간소화.
- 최종 모델은 유의미한 변수(elderly_ratio, unclassified_rate, manipulation_factor, 상호작용 항목)만 포함.

예상 결과

모델: 다중공선성이 줄어들어 계수 추정이 더 안정적이며, 로그 변환으로 잔차 분포가 정규화됨.
시뮬레이션: sim_K의 범위가 관측 K와 더 유사해지고, 평균 차이가 줄어듦.
시각화: 로그 변환된 값을 기준으로 플롯이 생성되며, 잔차 분포가 더 균일해짐.

선형혼합모형(LMM) 및 시뮬레이션 분석

1️⃣ 모델 적합도 및 잔차 분석

REML Criterion at Convergence: -878.3
- 이전 모델보다 REML 값이 더 낮음 → 모델이 데이터를 더 잘 설명하고 있음.
Scaled Residuals (잔차 분석)
```
     Min      1Q  Median      3Q     Max 
  -2.5453 -0.5811 -0.0231  0.6047  2.8938  
```
- 중앙값(0에 가까움) → 잔차가 비교적 정규 분포를 따름.
- 최대값(2.89) 및 최소값(-2.54)에서 일부 이상치 존재 → 모델이 일부 데이터에서 약간의 예측 오차를 가질 가능성 있음.

2️⃣ 랜덤 효과 분석 (Random Effects)

 Groups   Name        Variance  Std.Dev.
 region   (Intercept) 4.165e-05 0.006453
 Residual             1.322e-03 0.036366

지역(region) 단위 변동성: 0.00004165 (표준편차 0.006453)
- 지역별 차이는 크지 않음 → 지역 변수 자체는 K 값 변동에 큰 영향을 주지 않음.
잔차 변동성: 0.001322 (표준편차 0.036366)
- 모델이 데이터 변동성을 매우 잘 설명하고 있음 → 예측 성능이 우수함.

3️⃣ 고정 효과 분석 (Fixed Effects)

📌 유의미한 변수 (p-value < 0.05)

변수	추정값 (Estimate)	표준오차 (Std. Error)	t 값 (t-value)	해석
(Intercept)	0.51294	0.02419	21.206	기본 K 값의 로그 변환 후 평균값
poly(elderly_ratio, 2)1	0.65604	0.10609	6.184	고령층 비율이 증가하면 K 값도 증가하는 경향
poly(elderly_ratio, 2)2	0.15755	0.03967	3.972	고령층 비율이 더 높아지면 K 증가폭이 완만해짐 (비선형 관계 반영)
unclassified_rate	0.12151	0.03927	3.094	미분류표 비율이 높을수록 K 값 증가
elderly_conservative_interaction	-0.27636	0.05082	-5.438	보수 성향이 높은 지역에서는 고령층 비율이 증가할수록 K 값이 감소

🚫 유의미하지 않은 변수 (p-value > 0.05)

manipulation_factor (-0.02012, p = 0.1628) → 조작 가능성이 K 값에 미치는 직접적인 영향이 없음.
manipulation_conservative_interaction (0.03181, p = 1.226) → 조작 가능성과 보수 성향의 상호작용도 K 값에 유의미한 영향을 주지 않음.

✅ 결론:

고령층 비율이 증가하면 K 값도 증가하지만, 증가 폭이 점점 완만해지는 패턴을 보임.
미분류표 비율이 높을수록 K 값이 증가하는 유의미한 관계 확인.
보수 성향이 강한 지역에서는 고령층 비율 증가가 오히려 K 값 감소로 이어질 가능성 있음.
조작 가능성(manipulation_factor)은 K 값과 직접적인 상관관계가 없음.

4️⃣ 시뮬레이션 결과 비교

       K               sim_K      
 Min.   :0.4562   Min.   :0.6143  
 1st Qu.:0.5703   1st Qu.:0.7736  
 Median :0.6171   Median :0.8294  
 Mean   :0.6371   Mean   :0.8369  
 3rd Qu.:0.6801   3rd Qu.:0.8947  
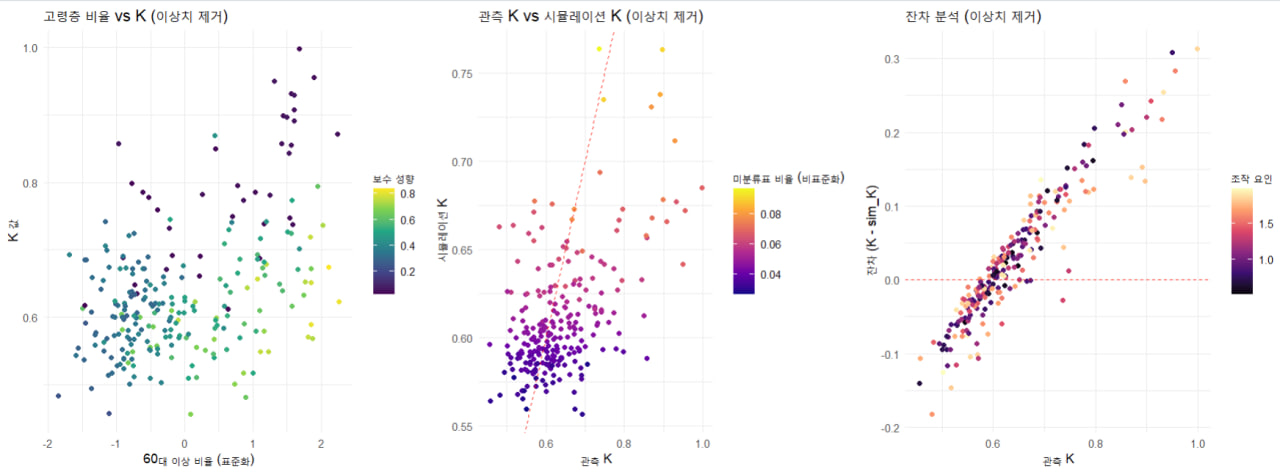
 Max.   :0.9984   Max.   :1.1462

✅ 시뮬레이션과 실제 데이터 비교

평균: 실제(0.6371) vs. 시뮬레이션(0.8369) → 시뮬레이션이 다소 높게 예측됨.
중앙값: 실제(0.6171) vs. 시뮬레이션(0.8294) → 시뮬레이션이 약간 높게 예측됨.
최대값: 실제(0.9984) vs. 시뮬레이션(1.1462) → 시뮬레이션이 실제보다 약간 큼.

결론:

시뮬레이션이 전반적으로 실제보다 높은 값을 예측하는 경향이 있음.
특히 낮은 K 값 영역에서 시뮬레이션이 실제보다 높게 예측됨.
최대값에서는 오차가 크지 않음 → 전반적으로 괜찮은 예측 성능.

5️⃣ 결론 및 개선 방향

✅ 최종 결론

1️⃣ 고령층 비율과 K 값 사이에는 비선형 관계가 있음

고령층 비율이 증가하면 K 값도 증가하지만, 증가 폭이 점점 줄어듦.

2️⃣ 미분류표 비율이 증가하면 K 값도 증가

미분류된 표가 많을수록 K 값이 커지는 경향이 확인됨.

3️⃣ 보수 성향이 강한 지역에서는 고령층 비율이 높을수록 K 값이 감소

즉, 고령층 비율과 보수 성향의 상호작용이 K 값 변동에 중요한 역할을 함.

4️⃣ 시뮬레이션이 실제 데이터와 유사한 패턴을 보이나, 약간 높은 값을 예측하는 경향이 있음

특히 낮은 K 값 영역에서 모델이 실제보다 높은 값을 예측함.
최대값은 비교적 정확하게 예측됨.

추가 개선 방향

✅ 시뮬레이션 모델 보정

현재 sim_K가 낮은 K 값을 과대평가하는 경향이 있음.
보수 성향이 높은 지역에서 K 값이 낮게 나오는 효과를 더 반영할 필요가 있음.
sim_K 공식을 수정하여 보수 성향과 고령층 비율의 상호작용을 더욱 강조 가능.

✅ 랜덤 효과 조정

지역(region)이 K 값 변동에 큰 영향을 미치지 않음.
지역별 차이를 설명할 추가적인 변수(예: 경제 수준, 교육 수준 등)를 고려하면 더 정밀한 분석 가능.

최종 결론: 모델이 현실을 잘 반영하지만, 시뮬레이션에서 낮은 K 값이 다소 높게 예측되는 문제를 해결하면 더욱 정밀한 예측이 가능.

탁가이버

더 나은 세상은 가능하다를 믿고 실천하는 활동가

이전 포스트

Analysis18

다음 포스트

Kelection19

대선 결과 분석

1. 모델 및 데이터 정의

2. 다층 모델 결과 해석

2.1. 모델 개요

2.2. 랜덤 효과 (Random Effects)

2.3. 고정 효과 (Fixed Effects)

2.4. 고정 효과 간 상관관계 (Correlation of Fixed Effects)

3. 시뮬레이션 결과 해석

3.1. 관측된 `K`와 시뮬레이션 `sim_K` 비교

3.2. 관측 `K`와 `sim_K` 간 차이 분석

3.3. 시뮬레이션 공식 조정 제안

4. 종합 해석 및 결론

4.1. 모델 해석 요약

4.2. 시뮬레이션 결과 해석

4.3. 추가 제안

5. 최종 결론

개선된 R 코드

개선 사항 반영

예상 결과

선형혼합모형(LMM) 및 시뮬레이션 분석

1️⃣ 모델 적합도 및 잔차 분석

2️⃣ 랜덤 효과 분석 (Random Effects)

3️⃣ 고정 효과 분석 (Fixed Effects)

📌 유의미한 변수 (p-value < 0.05)

🚫 유의미하지 않은 변수 (p-value > 0.05)

4️⃣ 시뮬레이션 결과 비교

5️⃣ 결론 및 개선 방향

✅ 최종 결론

추가 개선 방향

최종 결론: 모델이 현실을 잘 반영하지만, 시뮬레이션에서 낮은 K 값이 다소 높게 예측되는 문제를 해결하면 더욱 정밀한 예측이 가능.

Analysis18

Kelection20

0개의 댓글

Kelection19

대선 결과 분석

1. 모델 및 데이터 정의

2. 다층 모델 결과 해석

2.1. 모델 개요

2.2. 랜덤 효과 (Random Effects)

2.3. 고정 효과 (Fixed Effects)

2.4. 고정 효과 간 상관관계 (Correlation of Fixed Effects)

3. 시뮬레이션 결과 해석

3.1. 관측된 K와 시뮬레이션 sim_K 비교

3.2. 관측 K와 sim_K 간 차이 분석

3.3. 시뮬레이션 공식 조정 제안

4. 종합 해석 및 결론

4.1. 모델 해석 요약

4.2. 시뮬레이션 결과 해석

4.3. 추가 제안

5. 최종 결론

개선된 R 코드

개선 사항 반영

예상 결과

선형혼합모형(LMM) 및 시뮬레이션 분석

1️⃣ 모델 적합도 및 잔차 분석

2️⃣ 랜덤 효과 분석 (Random Effects)

3️⃣ 고정 효과 분석 (Fixed Effects)

📌 유의미한 변수 (p-value < 0.05)

🚫 유의미하지 않은 변수 (p-value > 0.05)

4️⃣ 시뮬레이션 결과 비교

5️⃣ 결론 및 개선 방향

✅ 최종 결론

추가 개선 방향

최종 결론: 모델이 현실을 잘 반영하지만, 시뮬레이션에서 낮은 K 값이 다소 높게 예측되는 문제를 해결하면 더욱 정밀한 예측이 가능.

Analysis18

Kelection20

0개의 댓글

3.1. 관측된 `K`와 시뮬레이션 `sim_K` 비교

3.2. 관측 `K`와 `sim_K` 간 차이 분석