
4. 19대 대선과 가설 1 & 2 요약
<더플랜>에서 제시한 K는 이항 분포 (Binomial distribution)를 적용하여 체계를 갖춘 것으로, 각 후보의 분류표와 미분류표 득표수가 각각 모두 크다고 가정한 후 기대값을 구한 것입니다. 그런데 19대 대선의 13명의 후보자 중에서 전국 250개 지역 모두에서 큰 득표를 했다고 볼 수 있는 후보는 세 후보이므로 K값을 후보1, 2, & 3에게만 적용합니다. 실제로는 득표 1, 2위를 한 당선자와 (후보1) 경쟁자 (후보2) 두 후보에게 적용하는 것이 선거 감시의 의도이지만, 가설을 검증하기 위해 세 후보를 비교합니다.
먼저 18대 대선처럼 하나의 예를 들겠습니다. 19대 대선에서 가장 미분류율이 높았던 곳이 11%이었는데, 이 곳은 60세 이상이 30% 정도인 지역입니다. 그런데 이 곳에서 나온 두 개의 K값은 1.06 (후보1/후보2) & 1.02 (후보1/후보3)로 각각 1에 가깝게 나타났습니다. 미분류율이 높은데도 두 개의 K값이 1에 가깝게 나온 점이 가설2의 예상과는 다름을 보여주는 또 하나의 사례입니다. 전체적인 면에서 19대 대선 결과를 세 가지로 요약하겠습니다.
첫째, 19대 대선에서 세 후보 사이의 K 값을 구해보면, 당선자 후보1과 경쟁자 후보2 사이에서 K=0.6, 그리고 후보1과 후보3 사이에서 K=0.8로 나타났습니다. 이 것은 가설1로 설명이 되지 않습니다. 즉, 세 후보의 미분류율이 같지 않다는 판단에 이르게 됩니다. 그러나 어떻게 미분류율이 후보마다 다르게 나오게 되었는지는 가설1로 설명할 수 없으므로 의문으로 남습니다. 반면에 가설2는 이러한 미분류율 차이를 노령층의 도장표로 설명하려고 시도합니다.
18대 대선에서는K>1로서 당선자가 상대 후보보다 미분류표에서 더 많이 득표함으로써 선출되었지만, 19대 대선에서는 K<1로서 당선자가 상대 후보보다 미분류표에서 덜 득표하였는데도 당선되었습니다. 즉, <더플랜>의 K는 선출된 후보가 상대 후보와 비교해서 미분류표를 통해 상대적 득표를 더 많이 또는 적게 했는지를 보여주는 척도로 이해하면 되겠습니다.
둘째, 가설2로 19대 대선의 미분류율을 제대로 설명할 수 있는지 살펴봅니다. 이를 위해서는 연령별 투표율과 후보 지지율 두 가지가 필요합니다. 18대 대선과는 달리 표2에 나타나 있듯이 60대 이상과 50대 (50~59)의 투표 성향이 달랐으므로 투표자들의 연령 그룹을60세 이상, 50대, 50세 미만 세 그룹으로 조정합니다. 모든 미분류표가 도장표라고 가정하면, 즉 미분류표에 정상표가 전혀 없다고 가정하면, 세 가지 연령 그룹에서 미분류표를 발생시키는 확률이 각각 6.6%, 2.9%, 2.5%로 계산됩니다.
여기에서 유의할 점은 이러한 확률값이 표2에 나와있는 연령별 투표율과 연령별 후보 지지율 두 가지에 의해 결정된다는 사실입니다. 달리 말하자면, 연령별 후보 지지율에 대한 여론 또는 출구 조사 결과에 따라 확률값들이 바뀔 수 있고, 또한 이에 대한 신뢰할만한 자료가 없다면 확률값들을 구할 수 없게 된다는 뜻입니다. 즉, 노령층 가설은 수량화 검증이 어려운 내용으로서 미분류표들을 미지의 영역으로 남게 하는 면이 있습니다. 이 점은 미분류표의 투명성을 약화시켜 공정성 의혹의 근거가 될 수 있으므로, 도장표 방지가 공정성을 지키는 데에 절대적으로 필요하다고 봅니다.
그런데 이 확률들을 250개 지역에 각각 적용해보면, 18대 대선처럼 각 지역의 미분류 비율을 제대로 설명하지 못합니다. 예를 들면, 19대 대선에서는 미분류표 비율이 실제로 3%~11% 사이로 나타난 반면, 가설2에 따른 연령별 확률로는 3%~5% 사이의 예상값이 나옵니다. 가설2가 심정적으로 받아들이기 쉽고 현실성이 있는 것으로 여겨지나, 충분한 설명을 하지 못하는 것으로 판단하게 됩니다.
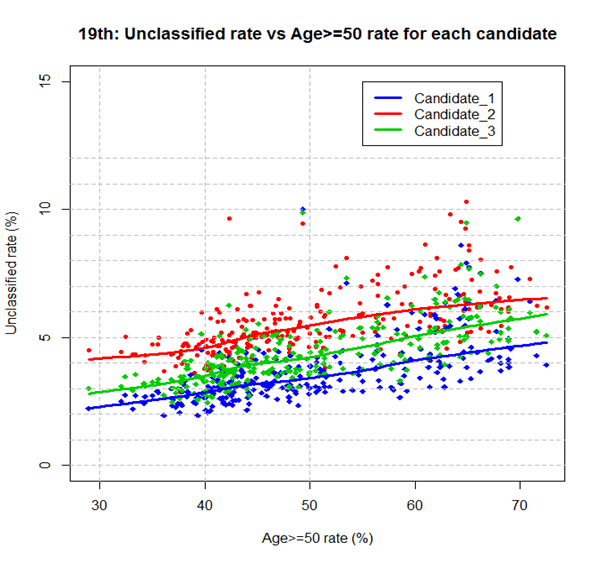
셋째, 가설2는 60세 이상과 50대 투표자들이 50대 미만 투표자들보다 미분류표를 상대적으로 더 많이 만들어 낸다고 설명하고 있으며, 앞에서 살펴본 확률로도 차이가 있음을 보았습니다. 가설2가 옳고 또한 출구 조사 연령별 지지율이 (표2) 신뢰할만 하다고 가정하면, 19대 대선에서 나타난 후보1과 후보3의 미분류율을 이해하기 어렵게 됩니다. 표2에 의하면 후보3은50세 이상 (60세 이상 포함) 연령 그룹에서 후보1보다 지지를 덜 받은 것으로 나타났기 때문에 미분류율이 후보1 보다 작게 나타나야 하는데 실제로는 더 높게 나타났습니다 (그림6). 따라서 이 현상도 가설2로 설명되지 않습니다.
5. 제안과 결론
1) K=1이 정상인가?
일반적으로 공정한 선거라고 할 때, 연령이 높다고 미분류표를 더 많이 만들어 내고, 또는 지지하는 후보에 따라 미분류표 비율이 달라지는 것을 정상적이라고 생각하기 어렵습니다. 공정한 선거와 공정한 선거시스템을 구별할 필요가 있습니다. 18대와 19대 대선 결과를 보면, 한국의 투표 방법이 (투표지 디자인과 도장 크기 등등) 미분류표 발생 과정에 많은 영향을 미치는 것으로 보입니다. 이것은 선거시스템의 문제입니다. 공정한 선거를 견인할 수 있는 공정한 선거시스템이 아니라고 볼 수 있습니다. 따라서 연령이나 후보에 따라 미분류율이 달라지는 것을 당연하다고 받아들이기 전에, 왜 달라지고 있는지 알아보고 그 원인을 제거함으로써 모든 후보의 미분류율이 같아지도록 개선하는 것이 절대적으로 필요합니다. 즉 K=1이 정상이 되는 투개표 환경을 만들어 나가면서, 전자개표기 사용을 감독할 수 있는 여건을 만들어 나갈 때에만 공정한 선거를 통계적으로 확인할 수 있게 됨을 강조합니다.
예를 들어 전자개표기를 사용하는 한국의 투개표 시스템과 비슷한 선거 시스템을 운영하는 다른 나라가 있다고 가정합니다. 그 나라에서는 투표지 디자인과 투표 표시 방법을 한국과 다르게 사용하고 있습니다. 이 선거에K를 적용하면 어떠한 결과가 나올까요? K의 어떤 값이 정상이 될까요? 한국뿐만 아니라 다른 나라의 선거까지 고려하면서 일반적 선거 검증 도구로 K가 적용된다면, K=1이 정상이라는 전제 아래 선거 결과를 분석하는 것이 적절할 것입니다.
다른 예를 들자면, K는 전체 미분류율과 상관이 없이 적용될 수 있습니다. 18대와 19대 대선에서 전국 합하여 대략 4% 정도의 미분류율이 나왔는데, 만약 이 미분류율이 20%로 커진다고 하더라도 K값이 1에 가까이 나온다면 정상적 선거가 이루어졌다고 판단할 수 있습니다. 전자개표기가 낙후되어 또는 준비가(calibration) 잘못되어 미분류율이 높아진다하더라도 각 후보별 미분류율이 같다면 (즉K=1), 기계적 문제일 뿐 개표의 공정성 문제는 아닙니다. 이 점 역시 한국에서 K=1이 정상이 되는 선거 환경을 만들어가야 하는 이유가 됩니다.
2) K=1이 되는 선거 환경을 만들 수 있을까?
결론부터 말하자면 가능합니다. 노령층 가설은 두 가지를 가정하고 있습니다. (1) 노령층이 도장표를 만든다; (2) 노령층이 특정 후보를 지지한다. 여기에서 (2)는 투표권을 가진 누구에게나 주어지는 권리이므로 반론의 여지가 없습니다. 그런데 (1)이 뜻하는 것은 “노령층은 도장을 제대로 찍지 못한다”라는 의미입니다. 노령층 가설과는 별도로 도장표를 만드는 투표자들의 특성에 따르자면, “보수는 도장을 제대로 찍지 못한다”[2], 또는 “특정 후보의 지지자들은 도장을 제대로 찍지 못한다”라는 해석이 나오기도 합니다.
그런데 (1)의 도장표는 방지할 수 있습니다. 즉 노령층도, 보수도, 또는 특정 후보 지지자들도 불필요한 책임에서 벗어날 수 있습니다. 투표지 디자인과 도장찍는 방법 등등 투표 방식의 개선을 통해서 가능합니다. 현재 사용되는 투표지와 도장을 그대로 사용한다면, 그림7에 있는 도구를 사용하여 지지하는 특정 후보에 도장을 제대로 찍을 수 있도록 도움으로써 도장표를 방지할 수 있습니다. 이 외의 여러가지 방법으로 도장표 방지가 가능할 것입니다.
다른 한 편, 도장표를 방지하여 K=1이 정상이 되는 선거 환경을 만든다면, 사전투표 감시 또는 개표 과정 감시에 따르는 비용과 수고를 줄이게 되는 장점이 생깁니다. 즉 K-값만 개표 후 확인하고, K-값이 1보다 큰 개표소에 대한 검증만 하면 됩니다.
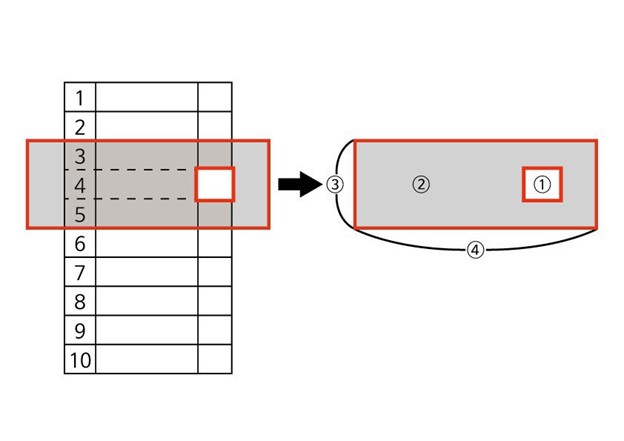
그림7: 투표지 도장 제대로 찍기를 돕는 도구
1) 도장을 찍을 수 있는 구멍.
2) 투명한 카버로 투표지를 볼 수 있으나 도장을 찍을 수 없음.
3) 높이는 후보 3명을 카버할 수 있을 정도.
4) 넓이는 손으로 만질 여백을 위해 투표지보다 넓게.
(아이디어: Kim, MH, 디자인: 프로젝 부)
승리방정식은 다음 장에...
