18대와 19대 대선 데이타에서 나온 K값에 대한 설명 (세 번째 자료)
작성자: 전희경, 현화신
작성일: 2017년 7월 30일
<더플랜>에서 제시한 K가 최근 2017년 5월에 치러진 19대 대선 결과 분석에 적용되었습니다[1,2]. 통계적 분석 방법이 선거에 응용되는 것을 반갑게 생각하면서, 이러한 검증 과정이 지속적으로 이루어져 앞으로 공정하고 투명한 선거 제도를 정착시키는 데에 기여하게 되기를 바랍니다. 그런데 <더플랜>에서 미분류표 분석의 도구로 거론한 K를 일부에서 오해하고 있는 것으로 보여 보충 설명을 하고자 합니다. 객관성을 유지하기 위하여 후보들의 이름보다는 당선자, 경쟁자 또는 후보1, 2로 표기합니다.
한국 18대 대선에서K=1.5로 나타났고, 이 것은 당선자가 경쟁자보다 미분류표에서 상대적으로 더 많이 득표하여 선출된 것을 의미합니다. 또한 전국 251개의 K값이 1.5로 모이는 현상을 발견하고K=1.5를 설명하는 방법의 하나로 전자개표기를 프로그램하는 시나리오를 세웠는데, 시뮬레이션 결과가 표1에 나타난 것과 같이 실제 선거 결과에 (251 개표소) 매우 가깝게 나타났습니다. 이 것이 의미하는 바는 <더플랜>에서 제시한 시나리오에 의해 18대 대선 결과를 재구성할 수 있다는 것입니다. 따라서 <더플랜>의 주제는 전자개표기 사용에 대한 경각심을 불러 일으키고, 더 나아가 개선 방법을 찾자는 것입니다.
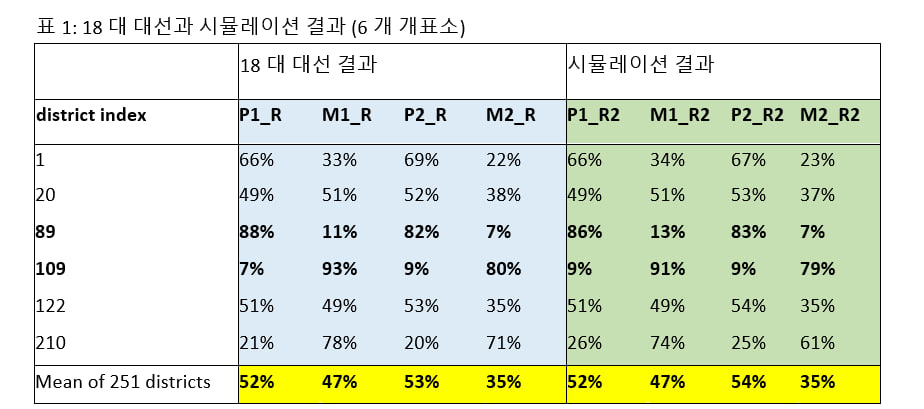
참고: 모든 지역에 대한 시뮬레이션 결과는 프로젝 부 사이트 ”2012 아카이브”에 첨부되어 있습니다. http://www.projectboo.com/archive/153432
18대와 19대 대선 결과와 관련하여 K를 이해하고 적용하는 방법을 아래와 같은 순서로 설명하겠습니다.
1. K란 무엇인가?
2. K값과 미분류표 생성에 대한 두 가지 가설 비교
3. 18대 대선과 가설 1 & 2 요약
4. 19대 대선과 가설 1 & 2 요약
5. 제안과 결론
K=1이 정상인가?
K=1이 되는 선거 환경을 만들 수 있을까?
18대 대선의 K=1.5값이 의도된 것인가?
6. 자료 출처
부록1 (K-test, 기대값과 분산)
부록2 (K-impact, 승리방정식)
1. K란 무엇인가?
<더플랜>에서 소개된 K는 통계적 테스트를 할 수 있는 척도입니다. 예를 들어, 암을 치료하는 새로운 약이 나왔을 때, 이 약의 효능을 판단하기 위하여 두 그룹을 가지고 실험을 합니다. 이 때 통계적으로 정립된 t-test는 두 그룹의 평균을 비교하면서 새로운 약의 효능이 있는지 또는 없는지 판단합니다. 이처럼 K는 두 후보의 미분류율을 비교하면서 당선자가 미분류표에서 상대적으로 득표를 더 많이 했는지 또는 아닌지 여부를 판단하는 테스트 방법으로 이해하면 되겠습니다 (즉, two-sample t-test for equal means versus two-candidate K-test for equal unclassified rates). K는 한국 선거시스템을 고려하여 만들어진 통계적 테스트 방법이지만, 그림1에 나타나 있는 것처럼 한국과 같은 투개표 시스템을 가진 다른 나라에서도 활용될 수 있는 일반화된 테스트 방법입니다.
좀더 통계적 내용을 소개하자면, 두 가지의 test statistic은 아래와 같이 정의됩니다.

Null hypothesis:
T: 두 개의 샘플 평균이 같다.
K: 두 후보의 미분류율이 같다.
테스트 결론을 내리기 위해서는 위 두 가지 검정 통계량(test statistic)을 주어진 데이타에 적용하여 얻은 값을 귀무가설(null hypothesis)에서 나오는 값들과 비교하게 됩니다. 그런데 T는 필요한 조건들을 만족하면 t-distribution을 따르고 있으므로 이를 바탕으로 두 개의 샘플 평균이 같은지 판단합니다. 반면에P1, M1, P2 & M2는 각각 이항분포를 따르지만, K는 특정한 분포를 따르지 않습니다. 따라서 두 후보의 득표수가 크다는 것을 가정하고, 두 후보의 미분류율이 같다는 귀무가설에서 나오는 기대값과 분산을 계산하였습니다 (부록1 참고). 이러한 통계적 테스트 접근 방식에 따라 두 후보의 미분류율을 같다고 놓는 것이 K의 통계적 특성을 찾는 데에 반드시 필요합니다. 주목할 점은 이러한 귀무가설에서는 K의 기대값이 지역 크기와 상관없이 항상 1이고, 분산은 지역 크기에 따라 달라진다는 것입니다. 예를 들어 어떤 지역에서 K=1.05 또는 K=0.94가 나왔을 때, 이 값들이K의 기대값 1과 같은지를 판단하려면, 부록1-(A)에 있는 분산을 적용하면 됩니다 (using log-normal distribution). 즉, 그 지역의 크기와 미분류율을 고려하여 판단하게 됩니다.
하지만 두 후보의 미분류율이 같지 않다면, K의 기대값과 분산 모두 지역마다 달라지게 됩니다 (부록1-(B) 참고) . 즉, 한국 18대 대선에서 나온 251개의 K값은 하나의 같은 분포에서 나온 것이 아니라, 각각 다른 분포에서 나온 것이 됩니다.
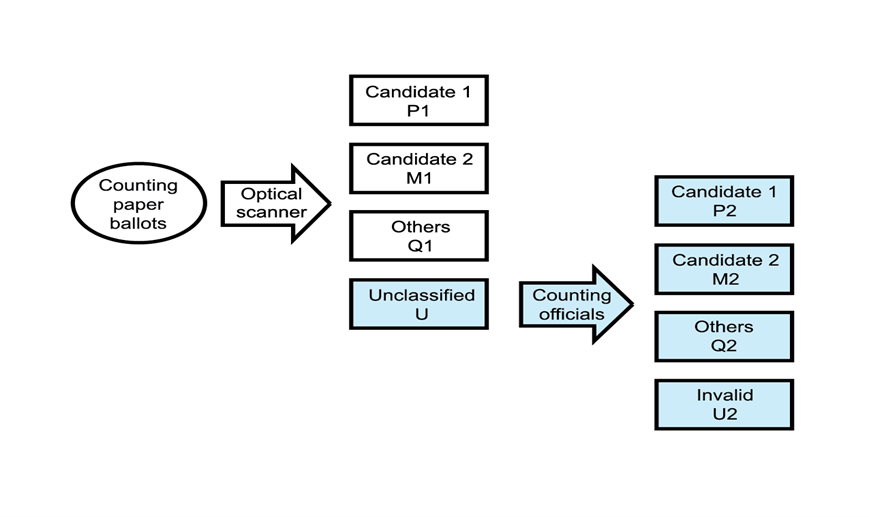
그림1: 투표지 분류 과정: (1) 전자개표기에 (optical scanner) 의해 먼저 분류되고; (2) 미분류된 투표지들은 심사집계부에 의해 재분류된다.
현재까지 논의된 바에 의하면 미분류표는 크게 두 가지로 분류되는데, 전자개표기 오류에 의한 “정상표”와 전자개표기가 판독할 수 없는 “도장표” (도장이 제대로 찍히는 않은 비정상표) 입니다. 분류표가 총 투표수의 96%를 차지하는 것에 비해 미분류표는 4%정도입니다. 따라서 박빙의 선거일 경우에 미분류표가 특정 후보의 당선 여부를 결정하는 데에 영향을 미칠 수 있습니다. 전자개표기가 정상적으로 작동하면, 분류표는 정상표임에 반해, 미분류표는 도장표로서 비정상표입니다. 그런데 미분류된 도장표는 선관위의 결정에 따라 유효 또는 무효표로 재분류 되는데, 선관위의 결정이 일정하지 않고 선거 때마다 바뀌는 부분이 있습니다. 따라서 박빙의 선거에서는 미분류표에 더 많은 관심을 갖게 되는 것이 당연합니다.
선거에서 K를 활용하고 해석하는 방법은:
먼저K=(미분류표에서 당선자/경쟁자)/(분류표에서 당선자/경쟁자)라 놓고 K-값을 구합니다.
(1) K = 1이면, 두 후보의 미분류율이 공정하게 같게 나타난 경우이므로, 즉 정상적인 선거가 이루어졌음을 제시하는 것이고;
(2) K < 1이면, 당선자가 미분류표에서 경쟁자보다 득표를 덜 하고도 선출된 것이므로, 즉 미분류된 비정상표에 의한 이득이 없으므로, 당선자 득표에 대한 의구심을 가질 필요가 없음을 제시하는 것이지만;
(3) K > 1이면, 당선자가 미분류된 비정상표에서 경쟁자보다 득표를 더 많이 하여 선출된 것이므로, 즉 미분류표에 의한 이득이 있으므로, 그 원인을 찾는 것이 필요함을 제시하는 것입니다.
또한 K의 특성을 다른 각도에서 찾을 수도 있습니다. 수학 식을 이용하여 K가 당선자 확정에 미치는 영향을 분석해 보았습니다 (부록2). 요약하자면 18대 대선에서 K=1.5이라는 값은, 분류표에서 (총 투표수의 96% 해당) 후보1이 (당선자) 후보2의 (경쟁자) 99% 이상만 득표하면 선출될 수 있는 수치라는 것을 승리 방정식 (winning equation)이 보여줍니다. 달리 말하자면, K값은 상황에 따라 미리 결정될 수 있고, 이 것을 전자개표기가 프로그램에 의해 실행할 수 있다는 가능성을 보여주는 것입니다. 하지만 이러한 플랜은 분류표를 제대로 확인하지 않을 때에 이루어진다는 점을 밝힙니다.
2. K값과 미분류표 생성에 대한 가설 비교
K값에 대한 기대값은 미분류표의 특성과 관련이 있습니다. 현재까지 논의된 미분류표에 대한 가설은 두 가지인데, 미분류표는 모든 후보에게 똑같이 발생한다라는 가설1과 (<더플랜> 가설) 또는 노령층에 의한 도장표에 의해 미분류표가 발생한다는 가설2 (이하 “노령층 가설” [3]) 있습니다. 지금까지 미분류표에 대한 공식 자료가 없기 때문에 두 가설 모두 검증이 필요하므로, 심정적 선택이 아니라 개연성과 현실성 여부를 비교하고자 합니다. 개연성은 선거 결과를 재구성할 수 있는 정도를 근거로 판단하는 것이 합리적이라 할 수 있겠습니다.
K값의 기대값은 가설1에 의하면 후보와 상관없이 항상 1이고 (이론적으로 증명됨), 가설2에 의하면 후보마다 달라지므로 1보다 크거나 작을 수도 있습니다. 따라서 가설1은 K=1이라는 기대값을 통해 두 후보의 미분류율이 같다 또는 다르다를 판단하는 근거를 제시합니다. 반면에 가설2는 판단의 기준이 없고 도장표 발생에 따라 달라지므로, 선거가 공정하게 이루어졌는지 그 여부를 판단할 수 있는 근거로 사용되지는 못합니다.
3. 18대 대선과 가설 1 & 2 요약
가설1은 <더플랜>에서 보인 시나리오의 근거입니다. 가설1과 시나리오는 연결되어 있지만 같은 내용은 아닙니다. 18대 대선을 재구성하기 위해 제안된 것이 시나리오인데, 이 시나리오가 가설1을 바탕으로 만들어진 것입니다. 그 결과 18대 대선에서 나타난 K=1.5를 바탕으로 계산한 확률들로 251 개표소에서 나온 두 후보의 분류표와 미분류표에서의 득표율 네 가지를 각각 매우 잘 재구성 할 수 있었습니다 (표1). 심정적으로 받아들이기 어려운 부분이 있을 수도 있으나, 18대 대선에서 전자개표기 프로그램이 절대적으로 불가능하다고 확인되지 않는 한, 가설1을 바탕으로한 시나리오를 틀렸다고 할 수 없겠습니다. 시뮬레이션과 실험으로 가설1의 개연성은 검증되었으나, 시나리오의 현실성에 있어서는 증명할 수 없는 부분이므로 가능성만 열어 놓습니다.
다른 한 편, 가설2는 심정적으로 받아들이기 쉬운 반면에 18대 대선 251개 개표소에서 나온 미분류율과K 값들을 제대로 설명하지 못하고 있는 아쉬운 점이 있습니다. 먼저 간단한 예를 들자면, 18대 대선에서 가장 미분류율이 높았던 곳이 12.5%이었는데 (50대 이상이 60%인 상대적으로 노령층이 많은 지역), 이 곳의 K값은 1로 나타났습니다. 노령층이 많으면 미분류율이 높고, 또한 미분류율이 높으면 후보1에게 더 많은 표가 갈 것이므로K>1로 기대되는 점에 어긋나는 사례입니다. 가설2의 개연성은 전반적으로 미분류율을 어느 정도 설명할 수 있느냐에 달려 있습니다.
가설2가 (노령층 가설) 18대 대선의 미분류표를 충분히 뒷받침해주지 못하는 점을 크게 세 가지로 요약하겠습니다. 첫째, 가설2의 핵심적 내용은 미분류표가 노령층에 의해 만들어졌다는 것이므로, 251개 지역에서 나온 미분류율을 노령층 분포[4]로 대략적인 설명을 할 수 있어야 합니다. 실제로는 미분류표에서 정상표들이 발견되었지만, 모든 미분류표가 도장표에 의해 전적으로100% 만들어졌다고 가정하고, 총 투표지 3천만표를 가지고 확률을 계산해 보았습니다 (샘플링이 아니므로 오류가 없음). 50대 이상의 투표자들이 (총 투표자의 44%) 미분류표를 만들 확률이 6.2%이고 50대 미만에서는(총 투표자의56%) 1.8%로 나와 50대 이상 투표자들의 미분류표 발생이 대략 3배 정도 높은 것으로 나옵니다. (q=0.062 & r=0.018, 확률 계산 자세한 방법은 프로젝 부 참고 http://www.projectboo.com/archive/153432)
그런데 이 확률들을 251개표소 각각의 노령층 분포에 (즉 50대 이상의 구성 비율) 적용해보면, 미분류율의 실제값이 2%~13%로 나온 반면에 가설 2 확률에 따른 예상값이1%~5% 정도입니다. 절반에도 못미치는 예상값이므로, 후보별 득표율 예상값도 실제값과 차이가 큽니다. 따라서 가설2는 현실성은 있어 보이나18대 대선을 충분히 설명하지 못합니다.
또한 19대 대선과 비교하기 위해 세 가지 연령 그룹으로 나누어 확률을 계산하여 보면, 60세 이상 (총 투표자의 23%), 50대 (21%), 50미만 (56%) 세 가지 연령 그룹에서 미분류표를 만들었을 확률이 각각 5.5%, 6.4%, 1.8%로 계산됩니다. 즉 50대가 60세 이상 그룹보다 미분류표를 더 많이 만든 것으로 나타납니다. 이 점도 가설2를 뒷받침하지 않는다고 볼 수 있습니다.
둘째, 가설2는 미분류표가 연령에 의해서 발생한다고 했는데, 18대 대선 결과를 보면 지지하는 후보에 따라 미분류표 발생 비율이 달라지는 것으로 나타났습니다. 예를 들면, 후보1의 지지자들이 후보2의 지지자들보다 미분류표를 더 많이 만들어냈습니다. 이 현상은 상대적으로 젊은 지역 (50대 이상 구성 비율이 20~40%인 지역들)에서도 나타났으므로, 미분류표는 연령뿐만 아니라 후보에 따라 발생한 것으로 이해하는 것이 적절합니다. 이 것은 서울 지역의 25개 개표소뿐만 아니라 (그림 2) 전국적으로 나타난 현상으로서 (그림3), 같은 연령 분포를 가진 지역이라도 지지하는 후보자에 따라 미분류표 발생율이 달라진 것을 볼 수 있습니다.
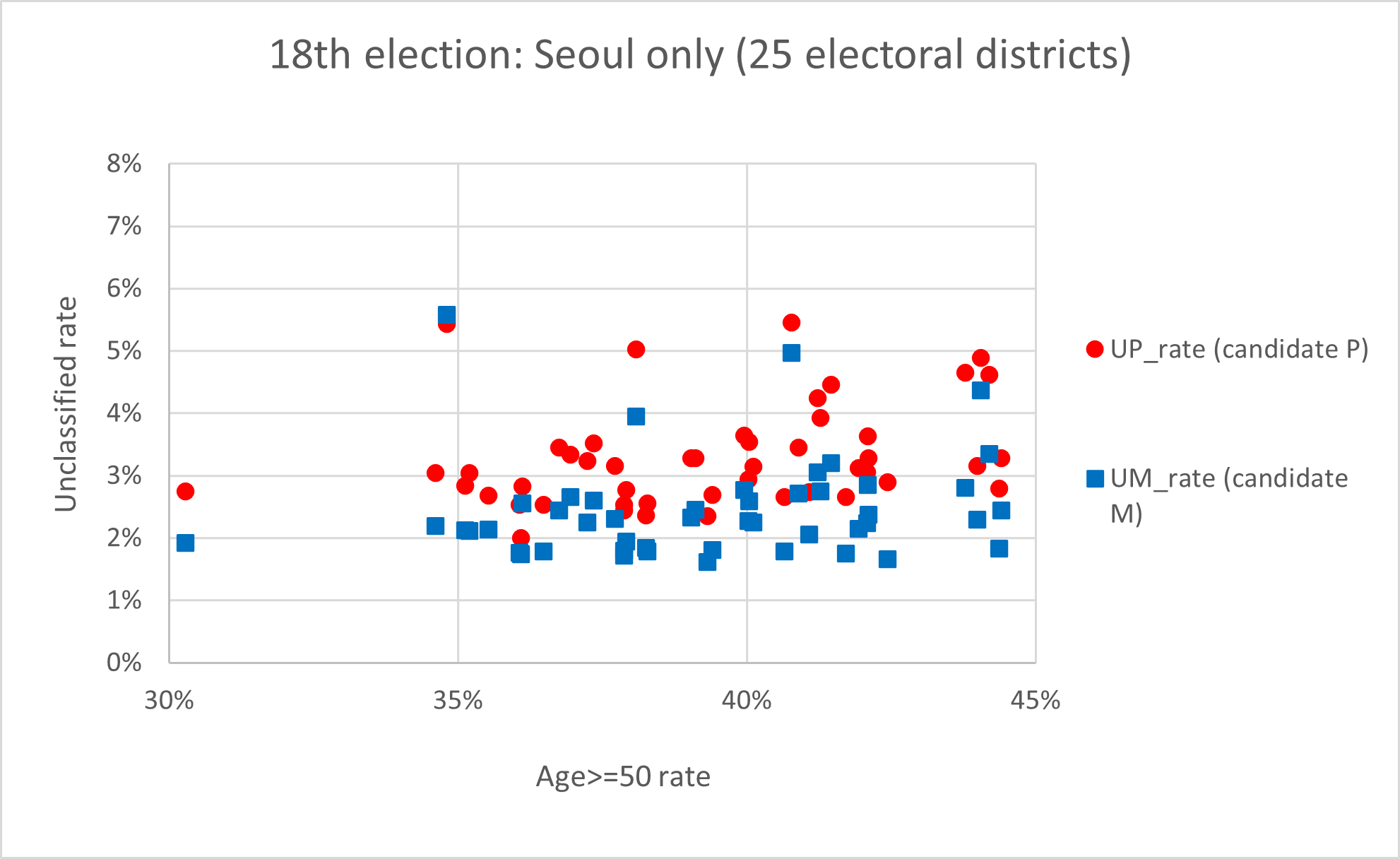
그림2: 18대선 서울지역에서 두 후보 사이의 미분류율 비교: (1) x값: 각 지역에서 50세 이상 투표자들의 비율 (%); (2) y값: 후보별 미분류율=P2/(P1+P2) or M2/(M1+M2).
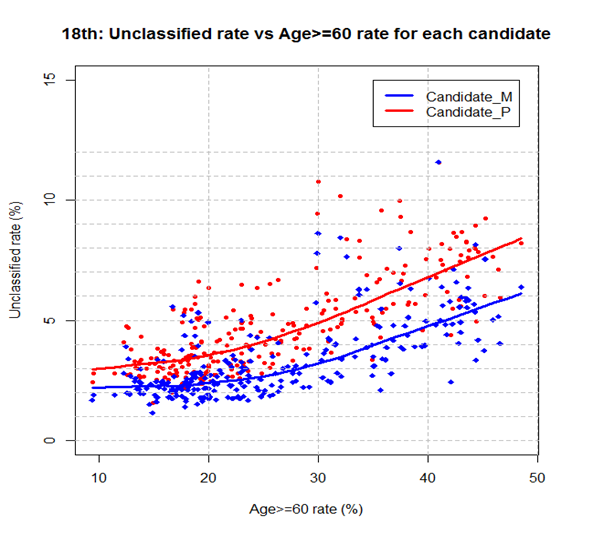
그림3: 18대선 전국에서 미분류율과 60세이상 노령층 비율 사이의 관계: (1) x값: 각 지역 60세 이상 투표자들의 비율 (%); (2) y값: 후보별 미분류율=P2/(P1+P2) or M2/(M1+M2).
그림3은 미분류율이 노령층의 비율이 높아짐에 따라 커지는 것을 보여줌과 동시에 노령층 분포만으로는 설명하지 못하는 점도 나타냅니다. 즉, 연령 분포와 상관없이 후보1 지지자들은 (빨간색) 후보2 지지자 (파란색) 보다 비정상표인 미분류표를 더 많이 만들었다는 것을 뚜렷하게 보여줍니다. 그런데 이 점을 가설2는 설명하지 못하고 있습니다. 이 부분을 “보수”로 설명하려면, 보수 투표자들은 보수가 아닌 투표자들보다 비정상적인 도장표를 더 많이 만들어 낸다는 사실을 인정해야 합니다.
셋째, 가설2는 미분류표가 노령층에 의해서 발생한다고 했는데, 특히 50대 (50세~59세)의 분포만 보면 이를 뒷받침하지 않습니다. 50대의 분포가 18-22%인 지역에서는 50대의 비중이 커져도 미분류율이 전반적으로 비슷하여 차이가 없는 것으로 나타났습니다 (그림4). 참고로 이 현상은18대뿐만 아니라 19대 대선에서도 나타났는데, 가설2를 뒷받침하지 않는 점을19대 대선에서 더욱 뚜렷하게 보여줍니다 (그림5).
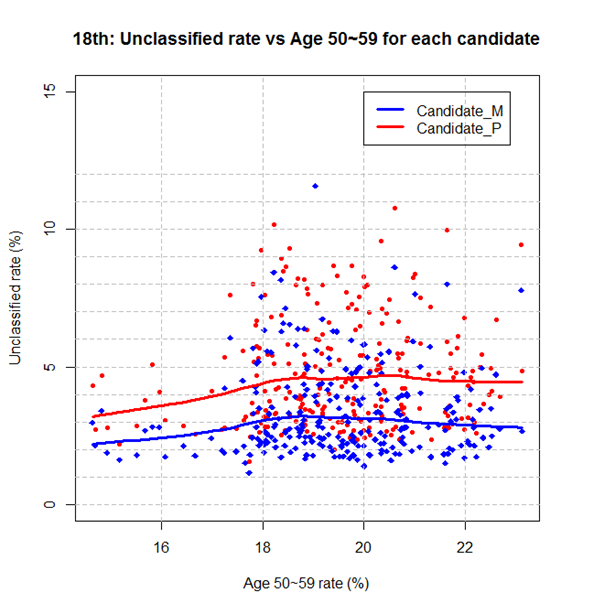
그림 4: 18대선에서 미분류율과 50대 연령층 비율 사이의 관계: (1) x값: 각 지역에서 50대 (50세~59세) 투표자들의 비율 (%); (2) y값: 후보별 미분류율=P2/(P1+P2) or M2/(M1+M2).
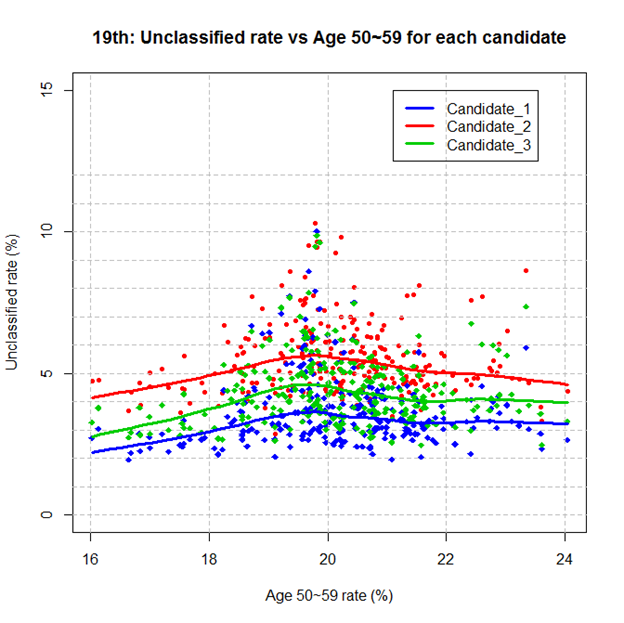
그림 5: 19대선에서 미분류율과 50대 연령층 비율 사이의 관계: (1) x값: 각 지역에서50대 (50세~59세) 투표자들의 비율 (%); (2) y값: 후보별 미분류율= M2/(M1+M2) in blue, H2/(H1+H2) in red or A2/(A1+A2) in green.
19대선 요약은 다음 장에...
