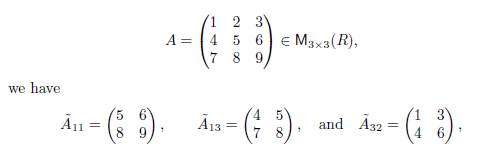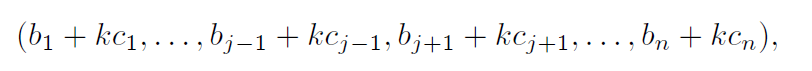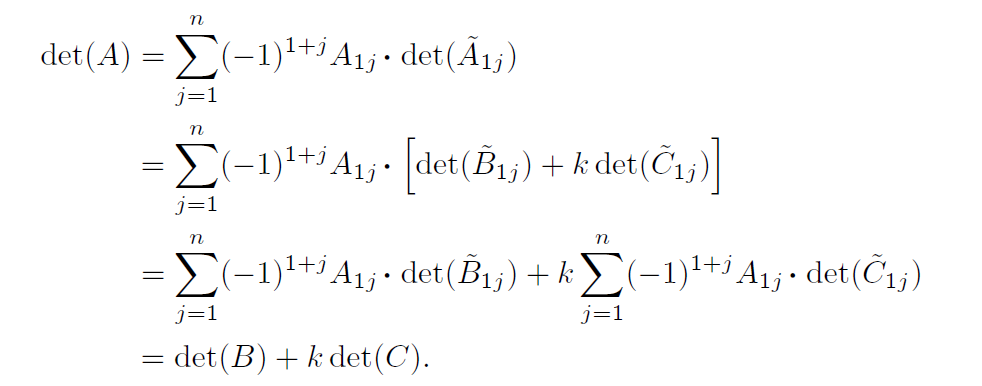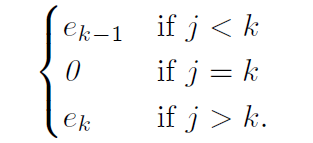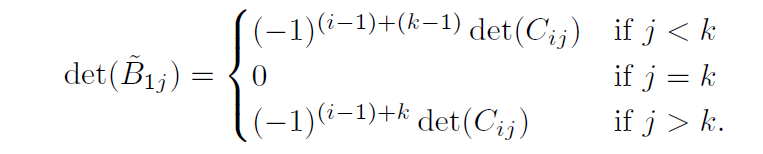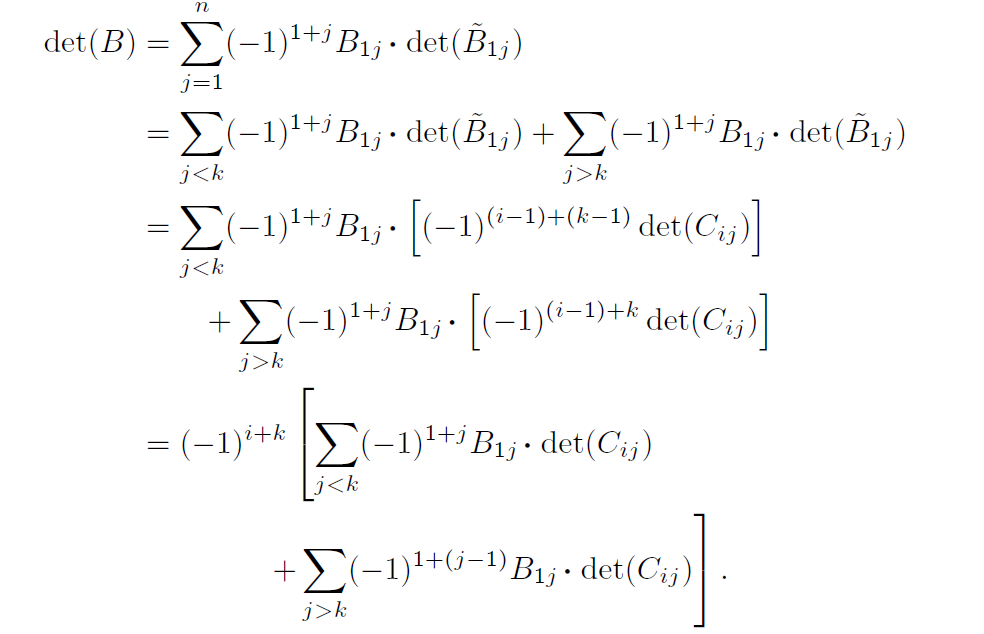0. Intro
행렬식은 일종의 함수로서 정사각행렬의 집합을 정의역으로 하고 스칼라를 함숫값으로 한다. 행렬식을 이용해 다양한 정리가 유도되기 때문에 짚고 넘어가도록 하자.
1. 2차 정사각행렬의 행렬식
우선 가장 간단한 2차 정사각행렬의 행렬식을 다루면서 행렬식에 대한 감을 잡아보자. 2×2 행렬의 행렬식은 다음과 같다.
정의 1. 체 F의 원소를 성분으로 하는 2×2 행렬 A가 다음과 같다고 하자.
(acbd)
이때 스칼라 ad−bc를 A의 행렬식이라 하며, det(A),∣A∣로 표기한다.
2×2 행렬의 행렬식은 고등학교에서 많이 다뤄봤기 때문에, 공식 자체가 낯설지는 않다. 다만, 그 성질에 대해 조금 더 살펴보자.
사실 행렬식은 함수이지만 선형함수는 아니다. 왜냐하면 det(A+B)=det(A)+det(B)이기 때문이다. 하지만 다음과 같이 특이한 선형적으로 보이는 성질을 가지고 있다.
정리 1. 함수 det:M2×2(F)→F는 2×2행렬의 다른 행이 고정되어 있을 때, 행렬의 각 행에 대하여 선형함수이다. 즉, 행렬 전체에 대한 선형성은 없지만, 한 행에 대해서는 선형적이다.
예를 들어 u,w,v∈F2, 스칼라 k에 대해 다음 식이 성립한다.
det(u+kvw)=det(uw)+k×det(vw)
이는 단순히 나열을 통해 증명이 가능한 정리이기 때문에 따로 정리하지는 않겠다.
행렬식의 또다른 중요한 성질은 가역행렬을 판단하는데 행렬식이 사용될 수 있다는 점이다.
정리 2. 행렬 A∈M2×2(F)에 대하여 A의 행렬식이 0이 아니기 위한 필요충분조건은 A가 가역행렬인 것이다. 특히, A가 가역행렬이라면, 역행렬은 다음과 같이 행렬식을 통해 구할 수 있다.
A−1=det(A)1(A22−A21−A12A11)
다음과 같이 증명할 수 있다.
다음과 같이 가역행렬 A가 주어져 있다고 하자.
A=(A11A21A12A22)
이때 가역행렬이므로 rank(A)=2이며, 즉, A11이나 A21은 0이 아니다.
만약 A11=1이면 2행에 1행의 A11−A21하여 다음 행렬을 얻을 수 있다.
(A110A12A22−A11A12A21)
기본행연산을 가한 것이기 때문에, 랭크는 보존되고, 그러므로 A22−A11A12A21=0이다. 결국 위 상황에서 det(A)=0이 된다.
2. n차 정사각행렬의 행렬식
2차 정사각행렬의 경우 공식을 외우면 됐다. 하지만 행렬은 2차 정사각행렬만 존재하지 않는다. 행렬식을 일반화해보도록 하자.
정의부터 이야기하면 다음과 같다.
정의 2. 행렬 A∈Mn×n(F)에 대하여 det(A)를 다음과 같이 귀납적으로 정의하자. (단, n=1이면 A=A11)
det(A)=j=1∑n(−1)1+jA1j⋅det(A~1j)
이때 스칼라 det(A)는 A의 행렬식이며 ∣A∣로 표기한다.
스칼라 (−1)1+jdet(A~1j) 는 A의 i행j열 성분에 대한 여인수(cofactor)를 의미한다.
이때 A~ij는 해당 행과 열을 제외한 나머지 성분으로만 구성된 일종의 부분행렬을 의미하는데 아래와 같이 표현될 수 있다.
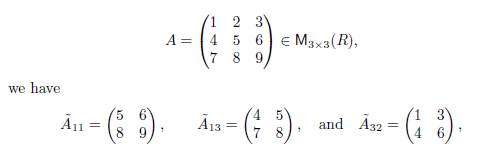
어떤 행렬 A에 대해 cij=(−1)1+jdet(A~1j)로 대입하고 공식을 적용하면 다음과 같을 것이다.
det(A)=A11c11+A12c12+…A1nc1n
다른 행을 써도 되지만, 결국 위의 식에 따르면, A의 행렬식은 A의 1행의 각 성분에 여인수를 곱하여 더한것이 된다. 즉, 행렬식은 행렬 A의 특정 행에 대한 여인수 전개라 할 수 있다. 2차 정사각행렬의 행렬식 공식도 이 식에서 유도되었다. 또한, n차 정사각행렬의 행렬식은 해당 행렬의 여인수를 2차 정사각행렬이 될때까지 반복하여 전개하여 계산하게 된다. 즉, 100×100 행렬이라면, 이를 계속 여인수 전개하여 2차 정사각행렬까지 내려가야한다. 이는 상당한 계산량을 요하게 된다.
3. 행렬 기본연산과 행렬식
n차 정사각행렬에 대해서도 2차 정사각행렬의 행렬식의 성질이 적용된다.
정리 3. n×n 행렬의 행렬식은 나머지 행이 고정되어 있을 때, 행렬의 각 행에 대하여 선형함수이다. 즉 1≤r≤n인 r에 대하여 다음 식이 성립한다. 이때 k는 스칼라이고, u,v와 각 ai는 행벡터이다.

이에 대한 증명은 다음과 같다.
n=1이면 당연히 참이 된다.
n≥2일 경우 다음과 같다.
n×n 행렬 A의 각 행을 a1,…,an이라 할 때, 어떤 r(1≤r≤n)와 u=(b1,…,bn)∈Fn,v=(c1,…,cn)∈Fn, 스칼라 k에 대하여 ar=u+kv라 하자. 이때, A의 r행을 u,v로 바꾼 행렬을 B,C라 하면, det(A)=det(B)+k⋅det(C)을 만족하면 된다.
- r=1일 경우 1≤j≤n에 대하여 자연스럽게 A~1j=B~1j=B~1j가 된다. 이때 행렬 식의 공식에 대입해보면
det(A)=j=1∑n(−1)1+jA1j⋅det(A~1j)=j=1∑n(−1)1+j(B1j+k⋅C1j)⋅det(A~1j)=j=1∑n(−1)1+jB1j⋅det(A~1j)+k⋅j=1∑n(−1)1+jC1j⋅det(A~1j)=j=1∑n(−1)1+jB1j⋅det(B~1j)+k⋅j=1∑n(−1)1+jC1j⋅det(C~1j)=det(B)+k⋅det(C) 그러므로 다른 행이 고정되어 있을 때, r=1이면 행렬식은 선형적이다.
- r≥2일 경우 1≤j≤n에 대하여 A~1j,B~1j,B~1j은 r−1행을 제외한 나머지 행은 같게 된다. 이때, A~1j의 r−1행은 다음과 같다.
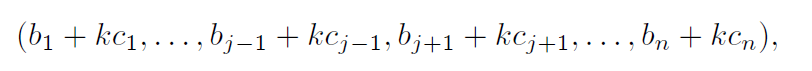
그런데 이는 결국 B~1j와 C~1j의 선형결합 꼴이 된다. 결국 다음과 같이 표현할 수 있게 된다. det(A~1j)=det(B~1j)+k⋅det(C~1j) 이는 결국 다음과 같은 증명으로 이어지게 된다.
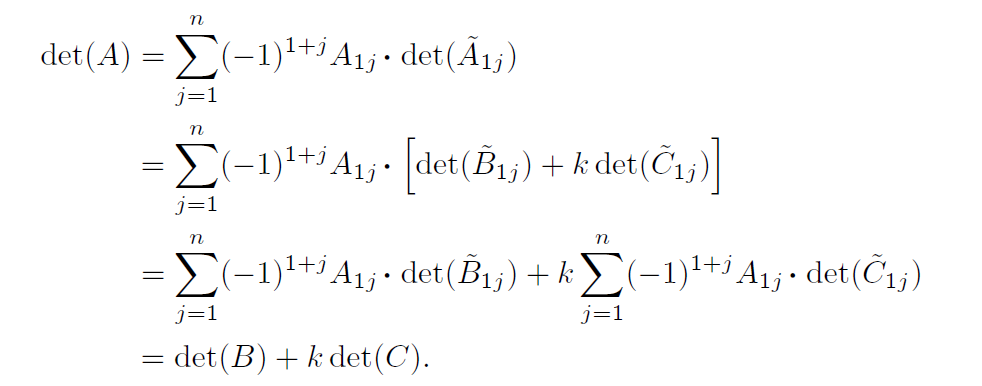
즉, n차 정사각행렬의 행렬식에 대해서도 다른 행이 고정되어 있다면 한 행에 대해서 선형성을 가지게 된다.
위의 연산은 행렬의 기본 행연산 중 2형 연산에 해당한다는 점을 기억하도록 하자.
여인수 전개를 할 때 지금까지 첫번째 행만 사용했는데, 다른 행을 사용할 수도 있다. 이에 대한 증명은 다음과 같은 과정으로 도출된다.
보조 정리 1. n≥2인 행렬 B∈Mn×n(F)의 i 행이 표준 기저ek 이면, det(B)=(−1)i+kdet(B~ik) 이다.
증명 :
n = 2이라면 자명한 사실이다.
n≥3 일때, (n−1)×(n−1) 행렬에 대해 위 보조정리가 성립한다고 가정하자. 이때 어떤 자연수 k(1≤k≤n)에 대하여 i행이 ek인 n×n 행렬 B를 생각하자. i = 1이라면 자명하게 성립한다.
1<i≤n일 때를 생각해보자. 각 j=k에 대하여, B의 1, i행, j, k열을 삭제하여 얻은 (n−2)×(n−2)행렬을 Cij라 하자. 즉, 첫번째 행을 지워서 기존의 행렬식 공식을 이용하고, ek인 행을 지워 우리가 원하는 바를 증명하려 하는 것이다. 각 j에 대하여 B~1j의 i-1 행은 다음 벡터의 꼴을 띄게 된다.
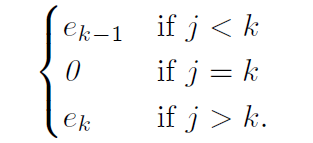
위의 식을 이용하면 det(B~1j를 쉽게 구할 수 있다.
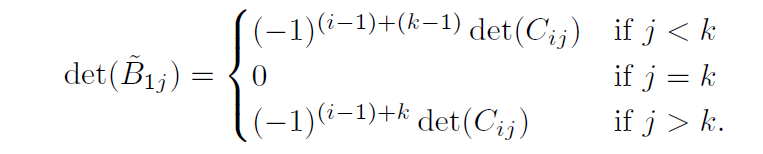
이제 det(B~1j를 알았으니 쉽게 det(B)를 계산할 수 있게 되었다.
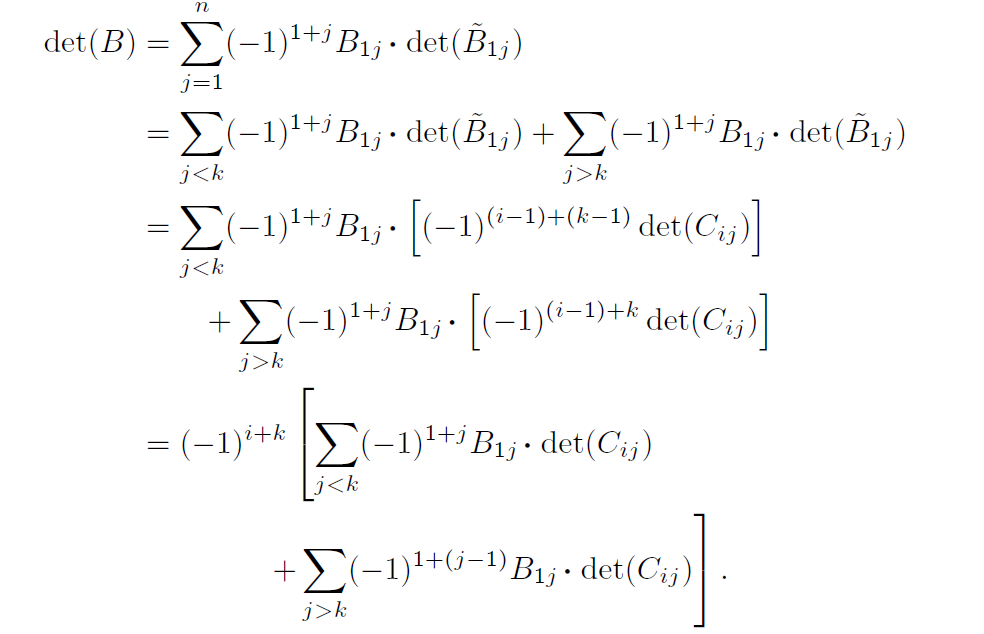
즉, 임의의 n×n 행렬에 대해 보조정리가 만족한다.
이제 이 보조 정리를 이용해 우리가 애초에 증명하고자 했던 아래 정리를 증명해보자.
정리 4. 정사각행렬의 행렬식은 임의의 행에 대하여 여인수 전개하여 구할 수 있따. 즉, A∈Mn×n(F)와 임의의 정수 i(1≤i≤n)에 대하여 다음이 성립한다.
det(A)=j=1∑n(−1)i+jAij⋅det(A~ij)
증명:
i = 1 이라면 기존의 행렬식과 동일하기 때문에 항상 참이다.
i>1으로 고정하여 생각해보자.. 이때, A의 i 행에 대해 표준 기저를 사용하여 ∑j=1nAijej 와 같이 전개할 수 있다.
이때 A의 i행을 ej로 대체하여 Bj 행렬로 나타내고, 위에서 증명한 정리 3과 보조정리를 이용하면 다음과 같이 det(A)를 표기할 수 있게 된다.
det(A)=j=1∑nAij⋅det(Bj)=j=1∑n(−1)i+jAij⋅det(A~ij)
이렇게 우리는 행렬의 어떤 행을 이용하여서도 행렬식을 구할 수 있게 되었다.
또한 다음과 같은 재밌는 정리 역시 성립하게 된다.
정리 5. 행렬 A∈Mn×n(F)의 어느 행의 모든 성분이 0이면 det(A) = 0이다.
이는 행렬식을 구하는 여인수 전개에서 각 tilde 행렬에 곱해지는 스칼라를 모든 성분이 0인 행으로 잡으면 자연스레 성립하게 됨을 알 수 있다.
유용한 다른 정리로는 다음과 같은 것이 있다.
따름 정리 A∈Mntimesn(F)의 두 행이 같으면 det(A) = 0이다.
이는 수학적 귀납법을 이용해 증명할 것이다.
n=2에서 두 행이 같다면, full rank가 성립하지 않고, 역행렬이 존재하지 않으므로 det(A) = 0이 된다.
n≥3일때 행렬 A∈Mn×n(F)에서 같은 값을 가지는 서로 다른 두 행을 r과 s행이라고 하자. 이때 r과 s가 아닌 다른 i행을 선택하여 여인수 전개를 하면 다음과 같을 것이다.
det(A)=j=1∑n(−1)i+jAij⋅det(A~ij)
이때 r과 s행의 값이 같기 때문에 자연스레 모든 i,j에 대해 det(A~ij)=0이 되어 det(A)=0이 된다.
이제 기본행연산의 남은 두가지 연산에 대해 증명하고 마무리하도록 하자.
제 1형 연산에 대해서 다음과 같은 정리가 가능하다.
정리 6. 행렬 A∈Mn×n(F)의 두 행을 교환하여 얻은 행렬은 B라 할 때, det(B)=−det(A)이다.
이에 대한 증명은 다음과 같이 보일 수 있다.
다음과 같이 A의 두 행 r,s를 두바꾼 행렬 B가 있다고 하자.
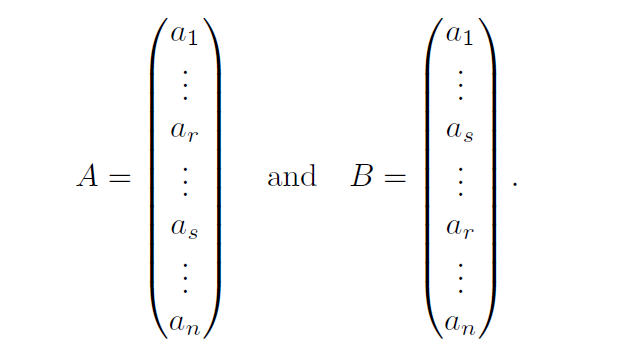
이때 다음과 같은 트릭을 써서 구성한 행렬의 행렬식을 구해보자. 이때 이전에 증명한 따름정리와 정리 3을 이용하면 된다.

마지막을 한 줄로 정리하면 0=det(A)+det(B)가 되고, 즉, det(A)=−det(B)가 된다.
제 3형 기본 연산에 대한 행렬식의 성질은 다음과 같다.
정리 7. 행렬 A∈Mn×n(F)와 A의 한 행에 다른 행의 스칼라 배를 더하여 얻은 행렬 B라 하자. 이때 det(A)=det(B)이다.
증명:
행렬 A의 s행에 r행의 k배를 더하여 얻은 n×n 행렬을 B라고 하자. 이때, A의 각 행을 a1,…,an이라 하고, B의 각 행을 b1,…bn이라 하자. 즉, bs=as+kar이다. A의 s행을 ar로 바꾼 행렬을 C라 하자. B의 s행에 정리 4을 적용하고, 따름 정리를 적용하면 다음과 같은 식이 성립하게 된다.
det(B)=det(A)+kdet(C)=det(A)
이상으로 행렬의 기본 행연산에 대한 행렬식의 정리를 모두 마쳤다. 정리하자면 다음과 같다.
- A의 두 행을 교환하여 얻은 행렬 B : det(B) = -det(A)
- A의 한 행에 0이 아닌 스칼라 k를 곱하여 얻은 행렬 B : det(B) = kdet(A)
- A의 한 행에 다른 행의 스칼라 배를 더하여 얻은 행렬 B : det(B) = det(A)
여기서 한가지 짚고 넘어가 이전에 어떠한 정사각행렬이든 기본 행연산을 통해 사다리꼴 형태로 변환할 수 있다는 것을 다뤘었다. 그런데 사다리꼴 행렬은 행렬식이 아주 간단하게 구해진다. 단순히 대각성분의 곱으로만 구성이 가능하다.