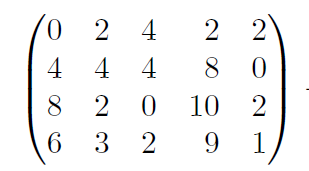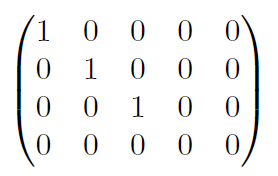0. 단사함수와 전사함수

단사함수와 전사함수는 이미 고등학교 수학 과정에 포함되어 있는 익숙한 내용이다. 고등학교에서는 2차원 공간으로 한정지어 배울 따름이다. 이제 이를 일반화하면 된다.

단사함수

단사함수란 일대일 함수를 의미한다. 즉 치역의 각 원소에 대응하는 정의역의 원소가 최대 1개인 함수를 의미한다.

위 그림에서 왼쪽은 단사함수가 아니고, 오른쪽은 단사함수다. $T:R^n \to R^m$인 선형변환을 가정할 때, 왼쪽은 여러 정의역의 원소가 치역의 0에 대응하고 있는 모습을 보인다. 하지만 오른쪽의 선형변환에선 정의역의 각각의 원소가 치역의 각각의 원소에 대응하고 있는 것을 알 수 있다.

전사함수

전사함수란 위로의함수(onto)를 의미한다. 이는 공역과 치역이 일치하는 함수를 의미한다. 2차원 공간상에서 생각해보면 2차함수는 치역이 공역보다 작지만, 1차 함수는 치역과 공역이 일치하게 된다.

위의 선형변환을 다시 생각해보면 좌측의 그림에선 어떠한 정의역의 원소를 선형변환하더라도 하늘색 평면으로 표현된 치역외의 다른 3차원 공역 상의 공간에 대응하는 원소가 되지 못하는 것을 볼 수 있다. 이에 반해, 우측의 그림에선 공역과 치역이 정확히 일치하는 모습을 보이고 있다.

0-1. 단사함수의 영공간

단사 함수의 영공간은 영벡터 하나로 이루어져 있다. 반대로, 영벡터만 영공간으로 가지는 함수는 단사함수이다. 증명은 다음과 같다.
벡터공간 $V, W$와 선형변환 $T:V\to W$에 대하여 다음을 통해 증명한다.

1. T가 단사함수이고, $x \in N(T)$라 가정하면, $T(x) = 0 = T(0)$이다. 이때, $T$가 단사이므로, x = 0이고, $N(T) = \{0\}$이다.
2. $N(T) = \{0\}, T(x) = T(y)$라 가정하자. 이때, $0 =T(x) -T(y)=T(x-y)$이므로, 다음이 성립한다.
   $x-y \in N(T) = \{0\} \leftrightarrow x - y = 0 \leftrightarrow x = y$
   그러므로 T는 단사함수이다.

0-2. 동치

다음과 같은 특별한 경우에 단사함수는 전사함수와 동치가 된다.

정리 1. 유한차원 벡터공간 $V, W$의 차원이 같을 때, 선형변환 $T: V \to W$에 대하여 다음 세 명제는 동치이다.
1. $T$는 단사이다.
2. $T$는 전사이다.
3. $rank(T) = dim(V)$

이에 대한 증명은 다음과 같다.
우선, $nullity(T) + rank(T) = dim(V)$를 상기하자.

이때 유한차원의 벡터공간이라는 점을 명심하자. 무한차원에 대해서는 성립하지 않는다.

1. 랭크

이전에 선형변환 $T:W \to V$에서 $R(T)$의 차원을 $T$의 랭크라 했다. 행렬이 선형변환과 연결되어 있다는 점을 생각하면 행렬의 랭크는 다음과 같이 정의할 수 있다.

정의 1. 행렬 $A \in M_{m \times n}(F)$에 대하여 $A$의 랭크는 선형변환 $L_A:F^n \to F^m$의 랭크로 정의하고, $rank(A)$로 표기한다.

이때, 행렬의 가역성은 랭크를 이용해 판단할 수 있다. $n \times n$ 행렬이 가역이기 위한 필요충분조건은 행렬의 랭크가 n이어야 한다.

이는 단사와 전사에 대해 설명하면서, 단사함수와 전사함수가 동치라고 했던 점을 명심하자. 그렇다면 $rank(A) = m (m < n)$이라는 것은 행렬 $A$가 선형변환으로서 전단사함수임을 의미하고, 이는 곧 $nullity(A) = \{0\}$임을 의미합니다. 이를 다시 행렬로 나타내면 $Ax = 0$인 벡터 $x$가 영벡터만 존재한다는 의미이므로 역행렬이 존재하게 됩니다. 자세한 내용은 뒤에서 더 다뤄보도록 하겠습니다.

그런데 행렬의 랭크는 단순히 선형변환의 랭크를 넘어 행과 열의 개념으로 생각해볼 수도 있다. 이때 랭크의 정의는 다음과 같다.

정리 2. 임의의 행렬의 랭크는 일차독립인 열의 최대개수와 같다. 즉, 행렬의 랭크는 그 열에 의해 생성된 부분공간의 차원이다.

이는 다음과 같이 증명될 수 있다.
임의의 행렬 $A\in M_{m \times n}(F)$에 대해 $F^n$의 표준 순서기저 $\beta$를 생각해보면, $\beta$는 $F^n$을 스팬하기 때문에 자연스레 다음 식이 성립하게 된다.

이때 $L_A(e_j) = Ae_J = a_j$이므로, 다음이 성립하게 된다.

즉, 행렬이 주어졌을때, 기본 열연산을 통해 행렬의 일차독립인 열의 개수를 구한다면, 랭크를 자연스레 구할 수 있다.

이때 가장 확실하게 일차독립인 열을 만드는 방법은 아래와 같이 서로 가지고 있는 0이 아닌 원소의 위치가 다른 열을 만드는 것이다. 만약 어떤 행렬이든 기본행렬연산을 이용해 아래와 같이 대각성분만 0이 아닌 원소를 가지는 꼴로 바꿀 수 있는지 확인할 수 있다면, 가역성을 검정할 수 있게 되는 것이다.

하지만 아래와 같은 행렬이

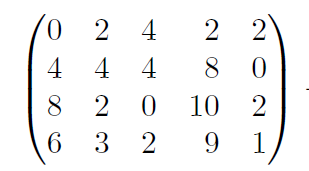
아래처럼 변형된다면

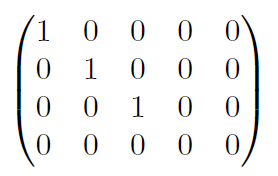
이는 full rank가 아니므로, 자연스럽게 역행렬이 존재하지 않는 행렬이 되는 것이다. 이때, 모든 행렬이 위와 같이 대각 성분으로 1 또는 0만을 가지는 부분 행렬이 단위행렬꼴인 모습을 가지도록 변형할 수 있다는 점을 명심하자.

1-1. 전치 행렬의 랭크

행렬 $A$가 있을 때, $A^T$의 랭크는 어떨까? 결론부터 말하면 $rank(A) = rank(A^T)$이다. 이는 위의 증명과 정리를 이용하면 간단하게 증명할 수 있는데 하나씩 해보자.

어떠한 행렬이든 유한 번의 기본행연산과 기본열연산을 가하면 다음과 같은 행렬$D$로 변환할 수 있다.

즉, 부분행렬이 단위행렬꼴인 모습으로 변환할 수 있는 것이다. 이를 수식으로 나타내면 다음과 같을 것이다.

그런데 기본행연산 혹은 기본열연산의 곱은 가역행렬이다. 이를 정리하여 $B = E_pE_{p-1}\dots E_2E_1, C = G_1G_2\dots G_q$로 나타내면 다음과 같은 모습이 된다.

정리 3. 즉, 어떤 $m\times n$행렬 $A$에 대해 $rank(A) = r$일 때, 다음을 만족하는 $m \times m$ 가역행렬 $B$와 $n\times n$ 가역행렬 $C$가 존재한다.

위의 정리에서 양 변에 전치행렬을 구해보면 다음과 같다.

그런데 B와 C가 가역행렬이므로 자연스럽게 $B^T$와 $C^T$도 가역행렬이다. 또한, 행렬 D는 이미 행과 열이 모두 선형독립의 꼴이다. 즉, $rank(C^TA^TB^T) = rank(A^T)$가 되고, 이를 최종적으로 정리하면 다음 모습이 된다.

결국 한 행렬의 전치와 원래 행렬의 랭크는 같다. 이는 랭크가 치역의 차원을 의미하고, 행렬이 선형변환과 연결되어 있다는 점을 생각해보면, 당연한 결과이다.
$L_A = F^n \to F^m$에서 역행렬을 선형변환으로 나타내면 $L_{A^T} = F^m \to F^N$이 되는데, $A$의 치역이 $A^T$의 정의역이 되기 때문이다.

---

참고

ratsgo's blog