[딥러닝] Neural Network #4

SSOYEONG·2022년 4월 14일

Deep Learning

목록 보기

5/14

Overfitting

Underfitting: training과 test errors 모두 높을 때
모델이 너무 간단 OR 충분히 training되지 않음
Overfitting: training error는 낮으나 test error는 높을 때
training 시 noise도 feature로 잡아 학습되었기 때문

Bias & Variance
Two main components of prediction error.

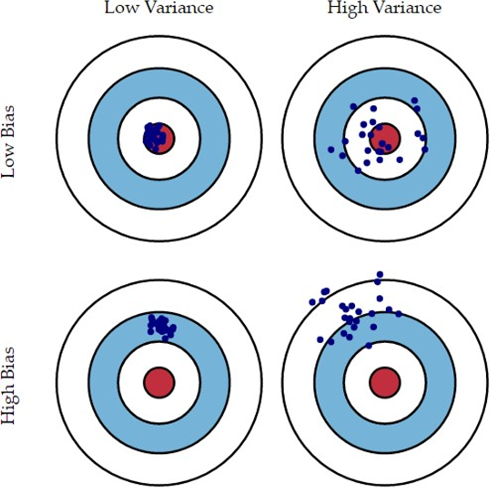
Bias: 모델이 너무 간단해서 생기는 에러
Variance: 얼마나 다양하게 모델을 예측할 수 있는지에 따라 생기는 에러 -> Generalization을 잘 하지 못한다.
Bias와 variance는 tradeoff 관계

How to prevent overfitting

1. Regularization

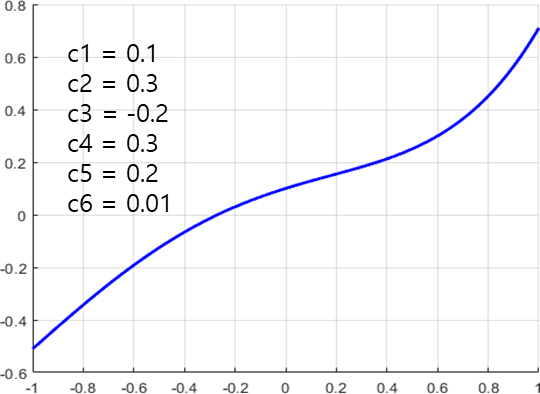
Model의 parameters가 0에 가까워질 수록 curve가 없다.
-> overfitting을 피할 수 있다.

Regularization: W값이 커지는 것을 방지한다.

Regulariazation을 한다
-> W가 작아지도록 학습시킨다.
-> Local noise가 학습에 큰 영향을 끼치지 않는다.
-> Outliers의 영향을 적게 받도록 한다.
-> 즉, Generalization에 적합한 특성을 갖게 만든다.

Regularization 종류

L1(Lasso) regularization

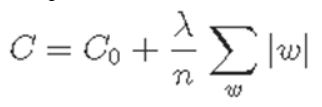
weight에 절댓값을 취해서 사용
람다로 regularization의 강도를 조절한다. 너무 작으면 overfitting 됨.

L2(Ridge) regularization

weight을 제곱해서 사용

Elastic net

L1, L2 방식 모두 적용

L1, L2 Regularization 차이
L1 : 덜 중요한 feature의 coefficient는 뺀다.
-> 특정 weight들은 0에 수렴해서 중요한 coefficients만 남는다.
-> Features가 많을 경우 feature selection에 유리하다.
미분 불가능하다는 단점
L2: L1보다 outliers에 둔감하다.

2. Dropout

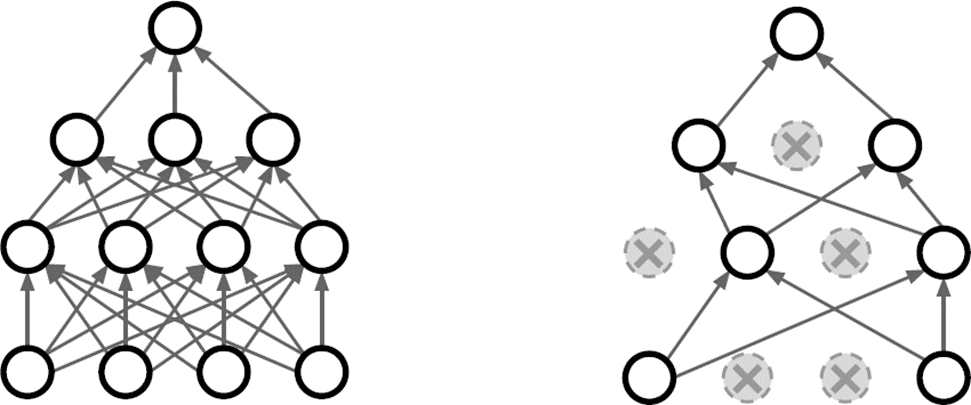
랜덤하게 몇몇 노드의 parameter 값을 0으로 만들어서,
forward pass에 참여하지 않도록 한다.
다음 iteration에 다시 랜덤하게 선택
일부 nodes에 bias 되는 것을 방지할 수 있다.

3. Batch Normalization

Normalization

[그림 1]과 같이 w에 치우쳐 있다면, w의 영향을 크게 받는다.
Normalization or Standardization을 겨쳐서 [그림 2]로 변환. W와 b가 고르게 반영되도록.

Covariate Shift

Covariate shift

이전 레이어의 파라미터 변화로 인하여 현재 레이어의 입력 분포가 바뀌는 현상

Internal covariate shift

레이어를 통과할 때마다 covariate shift가 일어나면서 입력의 분포가 약간씩 변하는 현상
Training을 진행할 수록 한 쪽으로 치우치게 되는 경우

-> 이를 해결하기 위해 Whitening을 도입하였으나 문제 존재.
Whitening

각 레이어의 입력을 N(0, 1)로 정규화하는 방법
(Benefit) training과 testing이 같은 distribution을 갖도록 변형시킨다.
(Problem) Costly to calculate / Bias가 사라진다.

Batch Normalization

Whitening의 문제를 해결하기 위해 도입
Solution for Internal covariate shift problem
평균과 분산을 조정하는 과정이 별도가 아니라, 신경망 안에 포함되어 학습 시 함께 조정하는 것.

For every mini-batch step
Step 1
각 layer에서 mini batch가 들어오면, 이를 N(0, 1)로 normalization한다.
Step 2
감마 곱하고, 베타 더한다. 이 감마와 베타를 training하면서 learning한다.
where 감마 and 베타 are parameters to be learned.

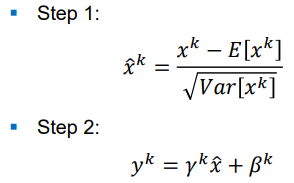
Training이 끝나면, 감마와 베타의 값을 고정시킨다.
왜? training 때는 가능. 근데 testing 시에는 적용하지 않기 때문에.
Testing 할 때는 고정된 평균과 분산을 이용해서 정규화한다.
Training 시 만들어두었던 sample mean과 sample varaiance를 통해 얻은 Moving Average을 사용한다.
The BN layer는 activation function 전에 위치한다.