1. 탐색(Search)
탐색은 많은 데이터들 가운데 원하는 데이터를 찾아가는 과정이다. 특히 트리 구조 및 그래프 구조의 안에서 탐색을 해야 할 경우 대표적으로 DFS와 BFS가 있는데, 우선 재귀를 이용한 DFS의 활용에 대해 먼저 살펴보겠다. DFS를 이해하기 위해 선행적으로 스택과 재귀함수를 다뤘었다. 이번에는 스택과 재귀를 이용하여 DFS, 즉 깊이 우선 탐색이 어떻게 진행되며 for문이나 while문과 다르게 어떤 방식으로 연산 횟수를 줄여주며 유동적인 모습을 어떻게 가지는지 살펴보자.
2. DFS
DFS는 깊이 우선 탐색이라 불리며 그래프에서 깊은 부분을 우선적으로 탐색하여 출력하는 알고리즘이다. 마지막 노드까지 내려가면 더 이상 깊이 탐색할 것이 없기에 마지막 노드를 출력하거나 체크한 후에 부모 노드로 다시 올라가고(Backtracking) 다른 자식 노드로 뻗어간다. 그래프는 아래와 같이 노드(Node)와 노드들 사이를 이어주는 간선(Edge)으로 이루어져있다. 그래프는 트리의 형식일 수도 있고 무작위 연결된(양방향 연결 혹은 방향 연결) 형식이 수도 있다.
알고리즘 문제의 형식마다 적용해야 하는 방법은 천차만별이지만 대표적으로 4가지를 염두해두고 DFS를 사용하는데, 순열, 중복순열, 조합, 부분집합을 구하는 방식으로 문제를 풀어나간다. 이번 챕터는 순열이며 각각의 방식에 따라 어떻게 DFS가 이용되는지 알아보자.
DFS는 함수가 호출되는 순간부터 순서대로 stack에 다음과 같은 형식으로 쌓인다
def DFS(n): if n == 5: return n += 1 DFS(n)# <- print(n, end=' ') DFS(0) 출력: 5 4 3 2 1
- 먼저 0이 n으로 입력되면 1을 더한 후 재귀로 DFS(1)을 호출한다. 이때 stack에는 [DFS(0)]가 쌓이고 '<-'까지만 진행된다.
- 다시 n에 1을 더하고 DFS(2)를 호출하면 stack에는 [DFS(0), DFS(1)]이 쌓이고 '<-'까지만 실행이 되고 다시 재귀가 일어난다.
- 이런 순서로 stack에는 [DFS(0), DFS(1), DFS(2), DFS(3), DFS(4)]가 쌓이고 마지막으로 n이 5가 된 순간 if 조건문에 의해 함수는 종료된다.
- stack은 후입선출이므로 DFS(4)가 다시 작동을 하는데 '<-'까지만 작동을 했으므로 그 다음 실행문인 print()문을 통해 수가 출력되고 함수가 끝이난다.
- stack가 빌 때까지 stack에 쌓인 호출문들이 다음 실행문인 print()문을 실행한다.
이때 보면 0부터 시작하여 1씩 더해가면서 트리를 탐색한다고 보았을 때 가장 나중의 5가 먼저 출력이 되는 것을 볼 수 있듯이, 재귀 함수가 마지막까지 진행되었을 때 break문을 실행하여 stack에 쌓인 재귀 함수들을 종료시켜나간다.
3. 순열(Permutation)
서로 다른 n개의 원소에서 r개를 중복은 없게 그리고 순서를 따져가며 나열하는 것을 순열이라고 한다. 예로 1, 2, 3이 있으면 3개 중 2개를 뽑는 방법은 (1, 2), (1, 3), (2, 1), (2, 3), (3, 1), (3, 2) 6개로 기호로는 nPr로 나타낸다. 이런 순열을 이용한 문제는 아래에서 확인해 보자.
4.1 문제
n개의 숫자카드가 주어지면 k개를 뽑을 수 있는 경우를 DFS를 이용하여 순열로 나열하고 몇 가지 경우의 수가 생기는지 출력하시오.
n = [2, 4, 6, 8], k = 2
4.2 풀이
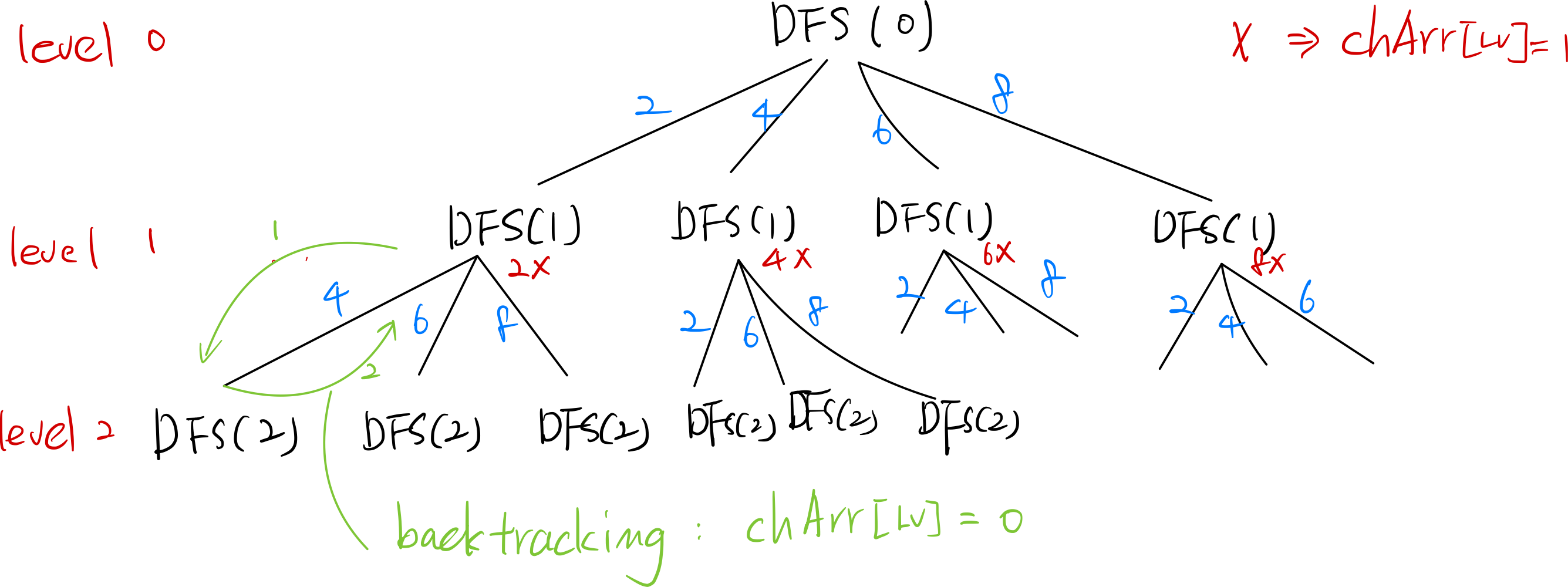
k값이 2로써 level이 2만큼의 깊이로 내려가서 탐색한 후 탐색한 값을 조건문을 통해 출력하는 방식이다.
1. DFS lv이 0일 때 else문의 for 반복문을 통해 인덱스로 순회하는데, 처음은 0으로 초기화가 되어있어 n의 첫번째 인덱스 값 0에 체크(chArr[lv]=1)되고 출력할 2를 per리스트에 담는다. 그 후 DFS(1)이 호출, 그리고 다시 아래의 반복문으로 내려가서 체크 배열에 인덱스 값 0은 체크가 되었기에 지나치고 체크가 되지 않은 인덱스 값 1에 체크를 한 후 per에 인덱스 1의 값 4를 입력한다. 다시 DFS(2)를 호출하는데 이제 lv은 2가 되었기에 if문에서 per이 출력되고 반복문의 인덱스 1, DFS(2)의 함수는 종료된다.(2 4 출력)
2. 인덱스 1, DFS(2)의 함수는 종료되었기에 DFS(2)의'<-'의 아래 실행문으로 내려가서 chArr을 다시 0으로 체크 해제한 후 인덱스가 1인 반복문 순서는 끝이나고 다음 인덱스 2값인 6이 내려온 후, 다시 체크되고 per에 담겨 다음 lv일 때 if문을 실행시킨다.(2 6 출력) 그리고 다시 반복 실행(2, 8 출력)
3. 숫자카드 '2'로 시작한 DFS(2)일 때 모든 반복문이 끝이나고 DFS(1)로 돌아와서 두 번째 숫자카드 DSF(1)일 때의 반복문의 첫 인덱스 값인 2의 다음인 '4 카드'가 시작된다.
#바깥 반복문 DFS(1) : 2, 4, 6, 8로 진행되고, 안쪽 반복문 DFS(2)는 각각의 DFS(1)일 때의 숫자 카드를 제외한 카드들을 반복한다. 4P2의 순열을 계산하면 '4 × 3 × 2 × 1 / 2 × 1 = 12'가지가 실행이 된다. k가 3이라면 lv3까지(DFS(3)) 내려 갈 것이고, 4 × 3 × 2 × 1 / 1 = 24'가지 경우의 수가 발생한다.
처음 DFS를 접하면 위의 설명도 이해가 잘 되지 않을 것이니, stack으로 그림을 그려가며 DFS의 실행 순서를 따라가면서 적어보자. DFS를 처음 접했을 때의 어지럽고 헷갈리는 진행은 그림을 그리고 순서를 따라갈 때마다 익숙해져 갈 것이다.def DFS(lv): global count if lv == k:# k개 만큼의 깊이로(2개를 뽑기에 2level까지 순회) 내려왔을 때 조건문에 의해 출력되고 DFS 종료 후 다음 DFS 실행 for i in per: print(n[i], end=' ') print() count += 1 # 하나의 순열이 만들어질 때 마다 수를 센다. else: for j in range(len(n)):# 반복문은 아래의 형식으로 진행된다. if chArr[j] == 0: # 체크한 인덱스에 있는 수는 중복이 되지 않도록 chArr[j] = 1 # 체크 per[lv] = j # 인덱스 번호를 저장. DFS(lv + 1)# <- 여기까지 진행 chArr[j] = 0 #체크를 푼다(Backtracking) 체크를 풀어야 다음 수가 들어올 수 있다. if __name__ == '__main__': n = [2, 4, 6, 8] k = 2 chArr = [0] * len(n) # 중복이 되면 안되기에 중복이 되지 않도록 체크 배열을 만들어 체크가 되어있으면 지나치도록. per = [0] * k# 순열을 담을 체크 배열 생성 count = 0 DFS(0) print('count: ', count) 출력: 2 4 2 6 2 8 4 2 4 6 4 8 6 2 6 4 6 8 8 2 8 4 8 6 count: 12