1. 에라토스테네스의 체(소수 판별)

그림출처:위키백과

고대 그래스 수학자 에라토스테네스가 발견한 에라토스테네스의 체는 소수를 찾는 방법이다. 위의 그림을 보며 진행순서를 보자.

1. 주어진 n까지의 모든 약수는 대칭을 이룬다는 것을 활용한다. 예를 통해 알아보자.

'8'의 경우 약수는 '1, 2, 4, 8'로
1 × 8 = 8
2 × 4 = 8
4 × 2 = 8
8 × 1 = 8
'20'의 경우 약수는 '1, 2, 4, 5, 10, 20'으로
1 × 20 = 20
2 × 10 = 20
4 × 5 = 20
5 × 4 = 20
10 × 2 = 20
20 × 1 = 20
위의 예시처럼 서로 대칭을 이루는 것을 볼 수 있다. 그래서 반을 나누어 살펴보면 , '8'의 경우 '2'의 배수만 확인하면 모든 약수를 확인할 수 있으며, 20의 경우 '2', '4', '5'의 배수만 확인하면 20의 모든 약수를 확인할 수 있다. 이처럼 주어진 n의 수가 커져도 약수 중 그 반에 해당하는 수들만 확인하면 n까지의 모든 약수를 확인 가능하다.(1 < 소수 < n))

2 제곱근을 활용한다.

이렇게 대칭점의 반의 수는 제곱근을 활용하여 확인할 수 있다. '20'의 제곱근은 4.47이고 여기에서 1을 더한 후 정수만 취하면 '5'가 되고 '5 이하' 정수들의 배수만 확인한다면 20의 약수는 모두 구할 수가 있다. 또한 '8'의 제곱근은 2.8로 1을 더해 정수만 취하면 '3'이므로 '3 이하'의 모든 정수들의 배수를 확인하면 된다.
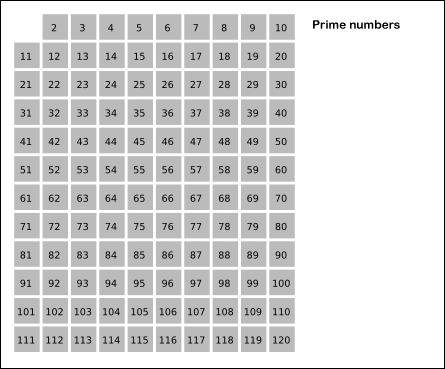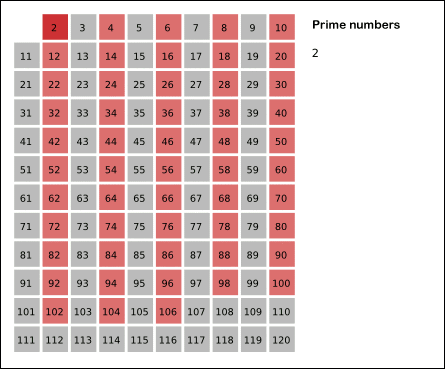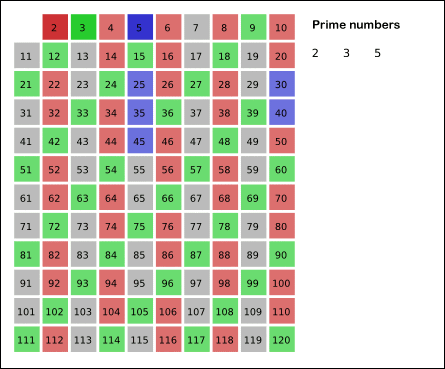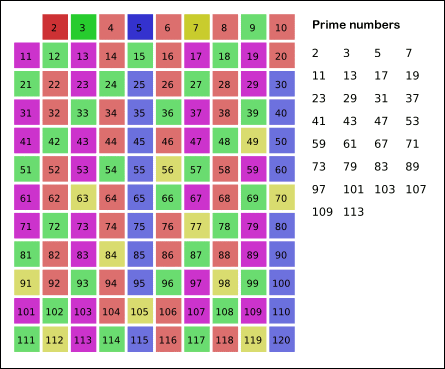
위의 그림은 '120' 이하의 소수를 찾는 순서를 보여주는데, '120'의 제곱근은 '10.95'로 여기서 1을 더한 후 정수 '11'만 취한 뒤, '11 이하' 정수의 배수만 확인하며 색을 채워나간다. 이렇게 색으로 칠하는 것을 코드 안에서는 체크 배열을 만들어 체크를 하는 식으로 확인을 하며 체크가 되지 않은 인덱스가 바로 숫자 소수이다.

3. 소수가 아닌 수들이 확인이 되었다면,

체크 되지 않은 곳(색이 칠해지지 않은 곳)은 어떤 수의 배수가 아니기에 즉, 1과 자신을 제외하고 어떤 수로도 나누어지지 않았으므로 소수가 되며 이 체크된 배열을 한 번의 반복문을 통해 체크가 되지 않은 인덱스 번호만 출력하면 된다.

2.1. 문제

백준 1929번 문제
고민을 통한 풀이 과정이 있어야 알고리즘 풀이 실력이 상승하니 먼저 설명처럼 코드로 구현해보도록 하자.
위에서 설명한 에라토스테네스의 체를 따라 코드를 작성해보자.
자연수 n, m이 주어지면 n에서 m 사이의 소수를 순차적으로 출력하는 문제이다.

2.2. 풀이

소수 판별 하기(에라토스테네스의 체)

# 먼저 공백을 두고 두 수를 입력한다.(문제예시: 3 16)
n, m = map(int, input().split())
# n부터 m까지 소수면 그대로 두고 소수가 아니면 1로 업데이트를 하여 판별할 수 있도록 0으로 초기화 된 리스트 배열을 생성한다.
chArr = [0] * (m + 1) # m까지 포함하기에 +1, 인덱스가 바로 해당 자연수와 같다.(인덱스 16은 자연수 16)
chArr[0] = chArr[1] = 1 # 0과 1은 소수가 아니기에 미리 체크(이유는 체크가 모두 끝난 후, 체크된 리스트 배열을 순회하며 0만 탐색 후 출력할 것이기 때문)
for i in range(2, int(m ** 0.5) + 1): # '제곱근(m**0.5)에 1을 더한 수'의 배수만 확인하면 된다. 
    if chArr[i] == 0: # 처음 수는 '2'로 소수이며 '2'부터 시작하여 배수들을 체크한다. 반복문 실행 중 이미 체크가 되어있으면 실행하지 않는다.(숫자 '4'는 숫자 '2'에 의해 이미 체크되었기 때문에 조건문의 실행문으로 내려오지 못한다)
        for j in range(i * 2, m + 1, i): # 체크가 되지 않은 수는 안쪽 반복문으로 내려와서 숫자 m까지 배수를 계속 체크해간다.
            chArr[j] = 1 # 체크하기
# 모든 체크가 끝났으면 시작 수 n부터 m까지 체크되지 않은 인덱스를 출력한다.(인덱스와 인덱스가 가리키는 수는 같다)
for i in range(n, m + 1):
    if chArr[i] == 0:
        print(i)
입력: 3 16
출력: 
3
5
7
11
13