[알고리즘] JS - 병합 정렬(Merge Sort)

박기영·2022년 9월 21일

JavaScript 알고리즘 자바스크립트

알고리즘 및 자료구조

목록 보기

4/6

병합 정렬(합병 정렬)

데이터들을 잘게 쪼갠 다음 하나로 합치는 과정에서 정렬하는 방법이다.

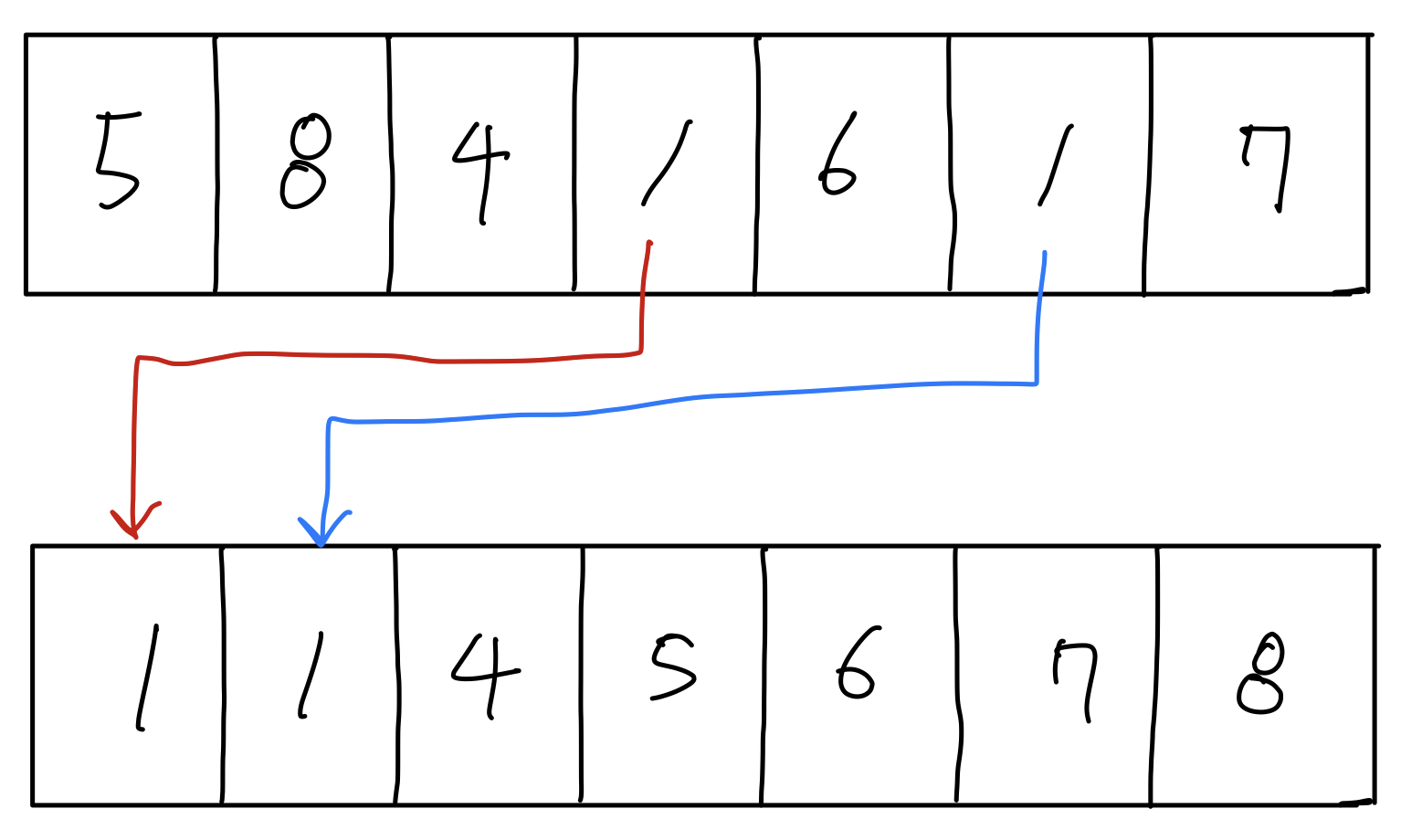
위 그림처럼 데이터를 반으로 쪼개나면서, 더 이상 쪼개지지않을 때까지 나눈 뒤
그들끼리 정렬을 하면서 다시 합병을 하는 과정을 거친다.

아래 영상을 보면 이해가 빠르다.

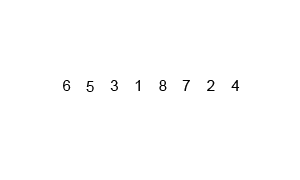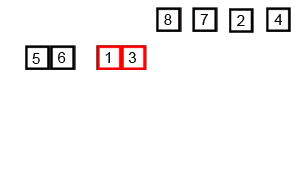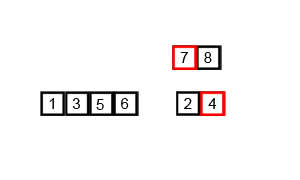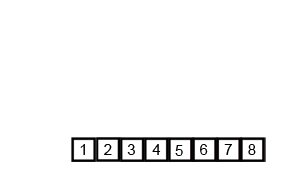
참고 이미지

Big O

O(nlog₂n) 의 시간복잡도를 가진다.

병합 정렬은 분할과 병합의 단계로 나눌 수 있는데, 분할 단계는 시간복잡도에 포함되지않는다.

데이터를 분할하고 병합하는 단계에서 log₂n 이 발생한다. 1/2씩 쪼개진 배열을 합치기 때문이다.
그 후, 데이터 개수만큼 크기 비교를 하는 과정에서 n 이 발생한다.
따라서, 최선의 경우든 최악의 경우든 모두 O(nlog₂n) 의 시간복잡도를 가지게 된다.

이 후에 배우게 될 퀵 정렬은 최악의 경우 O(n^2) 의 시간복잡도를 가지기 때문에
병합 정렬이 퀵 정렬보다 빠르다고 생각할 수 있는데, 항상 그렇지는 않다.
퀵 정렬이 병합 정렬보다 더 작은 상수 시간을 가지기 때문이다.

예를들어 어떤 배열을 콘솔 창에 하나씩 출력하는데 O(n) 이 걸리는데,
여기에 setTimeout을 활용해 1초의 딜레이를 줬다고 해보자.

이 경우 출력마다 1초를 기다려야하므로 실제 실행 시간은 느려진다.
그러나 빅오 표기법에서는 이런 상수들을 무시하기 때문에
그냥 출력과 setTimeout을 적용한 출력이 O(n) 으로 똑같이 표기된다.

이러한 이유로, 최악의 경우가 아닌 경우, 퀵 정렬이 병합 정렬보다 작은 상수값을 가지는 특징으로 인하여, 퀵 정렬이 좀 더 빠르다.

장점

어떤 경우든 O(nlog₂n) 의 시간복잡도를 가지기 때문에 데이터 분포에 영향을 덜 받는다.
항상 동일한 성능을 지니므로 좋은 성능을 기대할 수 있다.

단점

in place 알고리즘이 아니기 때문에, 정렬 시 별도의 메모리 공간을 필요로 한다.
정렬할 데이터가 많아지면 그만큼 이동 횟수가 증가하기 때문에 시간 낭비가 많아진다.

Stable

중복된 값이 정렬에 등장하더라도, 그들간 순서가 변하지않는 Stable 한 정렬이다.

참고 이미지

구현 방법

function mergeSort(array) {
  // array의 길이가 2보다 작으면 원소가 한 개이므로
  // 더 이상 쪼개지 않아, 그대로 배열을 반환한다.
  if (array.length < 2) {
    return array;
  }

  // 중앙을 기준으로 배열을 반으로 나눈다.
  // 짝수라면 딱 맞아떨어지지만, 홀수라면 5/2 = 2.5이므로 floor를 통해 2로 낮춰준다.
  // 2번 인덱스는 3번쨰 원소를 의미한다는 점에 주의!
  const mid = Math.floor(array.length / 2);

  // 왼쪽에 둘 배열을 생성한다. 0부터 mid - 1 인덱스까지이다.
  const left = array.slice(0, mid);

  // 오른쪽에 둘 배열을 생성한다. mid부터 끝까지의 인덱스이다.
  const right = array.slice(mid);

  // 재귀 호출을 통해, 더 이상 쪼개지지 않을 때까지 쪼갠다.
  // merge 함수로 정렬해서 합쳐주면 된다.
  return merge(mergeSort(left), mergeSort(right));

  function merge(left, right) {
    // 정렬 결과를 담을 배열
    const resultArray = [];

    // left와 right 배열의 앞 부분부터 비교를 해야하므로
    // 각각 0번 인덱스부터 시작하도록 설정한다.
    let leftIndex = 0;

    let rightIndex = 0;

    while (leftIndex < left.length && rightIndex < right.length) {
      // left 배열과 right 배열의 앞 부분부터 비교를 시작한다.
      // 만약, right 배열의 값이 더 크면
      if (left[leftIndex] < right[rightIndex]) {
        // resultArray에 left 배열의 값이 들어간다.
        // left가 더 작은 값이니까 더 앞에 정렬되야하기 때문이다.
        resultArray.push(left[leftIndex]);

        // left 배열에서 앞 부분이 처리된 것이므로, leftIndex를 증가시켜
        // 다음 순서의 값을 가져오도록 준비시킨다.
        leftIndex++;
      } else {
        // 만약, left 배열의 값이 더 크면
        // resultArray에 right 배열의 값이 들어간다.
        // right가 더 작은 값이니까 더 앞에 정렬되야하기 때문이다.
        resultArray.push(right[rightIndex]);

        // right 배열에서 앞 부분이 처리된 것이므로, rightIndex를 증가시켜
        // 다음 순서의 값을 가져오도록 준비시킨다.
        rightIndex++;
      }
    }

    // resultArray에 들어간 값(정렬된 값)과 left에 남아있는 값, right에 남아있는 값을 연결해서 반환한다.
    // 위 while문에서 left, right 연산이 전부 끝나면 둘 중 하나가 비어있기 때문에
    // 이렇게 연결해줘도 무관하다.
    return resultArray.concat(left.slice(leftIndex), right.slice(rightIndex));
  }
}

console.log(mergeSort([5, 4, 3, 2, 1]));