[알고리즘] JS - 삽입 정렬(Insertion Sort)

박기영·2022년 9월 21일

알고리즘 및 자료구조

목록 보기

3/6

삽입 정렬

삽입 정렬(Insertion Sort)는 왼쪽에서 오른쪽으로 가면서 각 요소를 왼쪽 요소들과 비교하여 알맞은 자리에 삽입하는 형식을 정렬 방법이다.

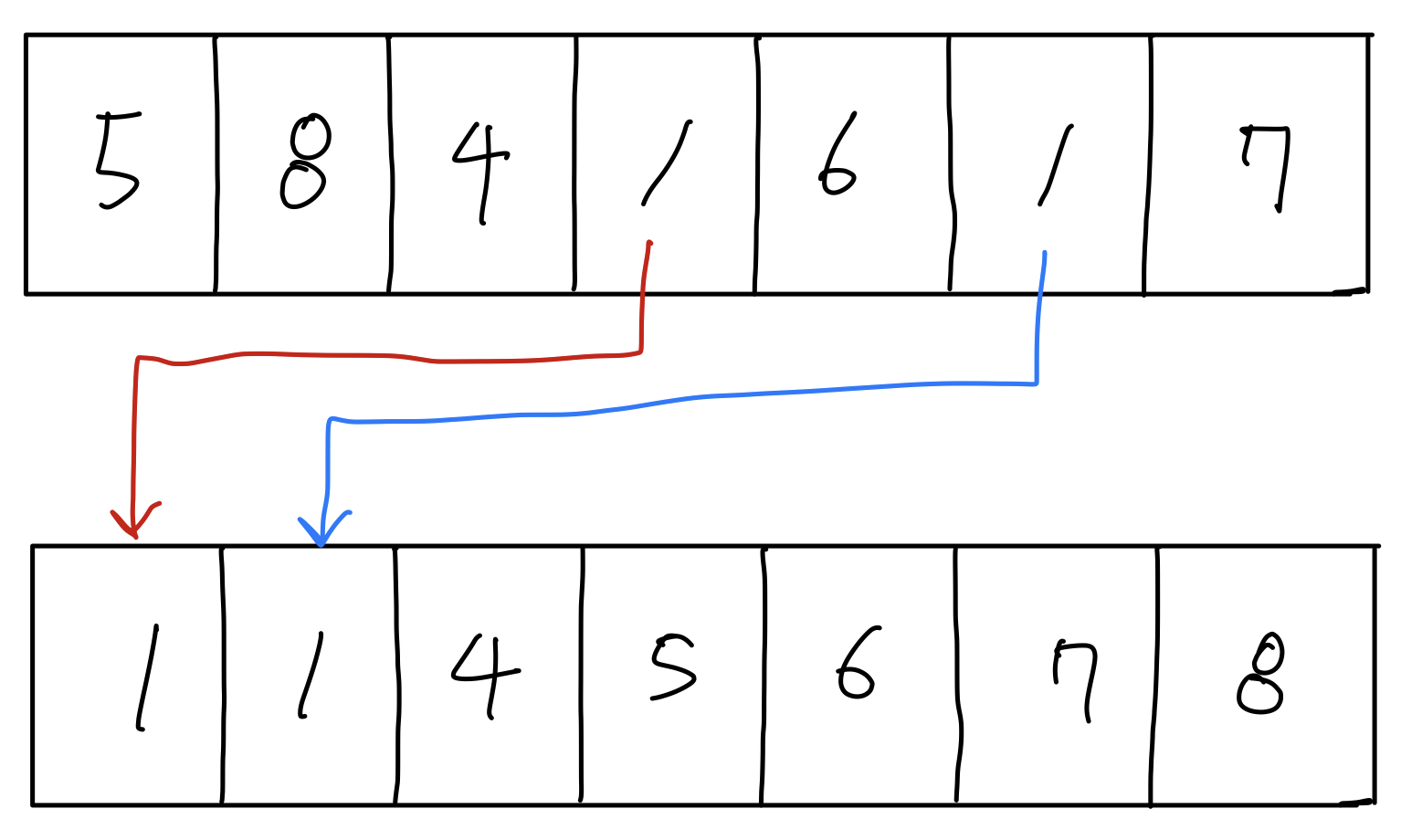
참고 이미지

위 그림처럼 붉은색 요소(오른쪽 요소)를 회색 요소(왼쪽 요소)와 비교하면서 시작된다.
1회차에서는 3보다 7이 크기 때문에 그냥 지나간다.
2회차에서는 3,7보다 2가 작기 때문에 가장 앞으로 옮겨진다.
3회차에서는 2,3,7 중 5는 3과 7 사이로 옮겨진다.
...

이런 식으로 정렬이 진행된다.
항상 왼쪽 비교 대상 데이터들이 정렬되어있다는 전제하에 진행된다.

Big O

O(n^2)의 시간복잡도를 가진다.
이미 정렬된 배열의 경우 O(n)의 시간복잡도를 가진다.
버블 정렬과 동일하다.

장점

버블 정렬과 같은 장점이 있다.

in place 알고리즘이므로 메모리가 절약된다.

구현이 쉽다.

이미 정렬된 데이터를 순회하는 경우 O(n) 의 시간복잡도를 가지므로 정렬 여부를 테스트하는 용도로 사용될 수 있다.

단점

자료의 개수가 많아지면 그 제곱만큼을 순회해야하므로 성능이 좋지 않다.

Stable

버블 정렬과 마찬가지로, 중복된 값이 있더라도 그들 간은 배열 순서가 바뀌지 않으므로
Stable 한 정렬이다.

참고 이미지

구현 방법

function insertionSort(array) {
  for (let i = 1; i < array.length; i++) {
    // 붉은색(오른쪽 원소)을 선택한다.
    // i가 0이 아닌 1로 시작하는 이유이다.
    let cur = array[i];

    // 회색(왼쪽 원소) 중 가장 오른쪽의 인덱스를 통해 개수를 파악한다.
    // ex) i가 1이면 left는 0이므로 1개...
    let left = i - 1;

    // 왼쪽에 남아있는 원소의 개수가 0 이상이면서
    // left번 인덱스에 있는 요소값이 cur 요소값보다 크다면
    while (left >= 0 && array[left] > cur) {
      // left번 인덱스 값을 left + 1번 인덱스에 넣는다.
      // 즉, 붉은색을 회색의 가장 오른쪽 부분과 교체한다.
      array[left + 1] = array[left];

      // left를 하나씩 줄여나간다.
      // 회색의 가장 오른쪽부터 비교를 시작해나간다는 뜻.
      left--;
    }

    // while문이 종료되면 연산이 마무리된 left에 1을 더한 자리에 cur 값을 넣는다.
    // ex) left가 0이고 cur값이 가장 작은 숫자였다면 결국 left는 -1로 연산이 마무리되므로
    // left + 1 = 0번 인덱스가 되며, 그 자리(0번 인덱스)에 cur 값을 넣는 것이다.
    array[left + 1] = cur;

    console.log(`${i}회전: ${array}`);
  }

  return array;
}

console.log(insertionSort([5, 4, 3, 2, 1]));