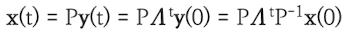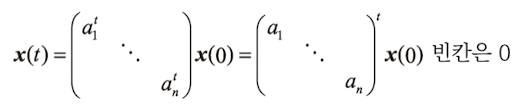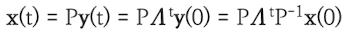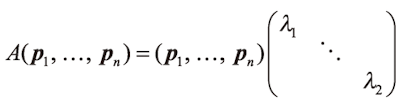프로그래머를 위한 선형대수(4)

4장) 고유값, 대각화, 요르단 표준형(폭주의 위험이 있는지)

• 4.1) 문제 설정 : 안정성

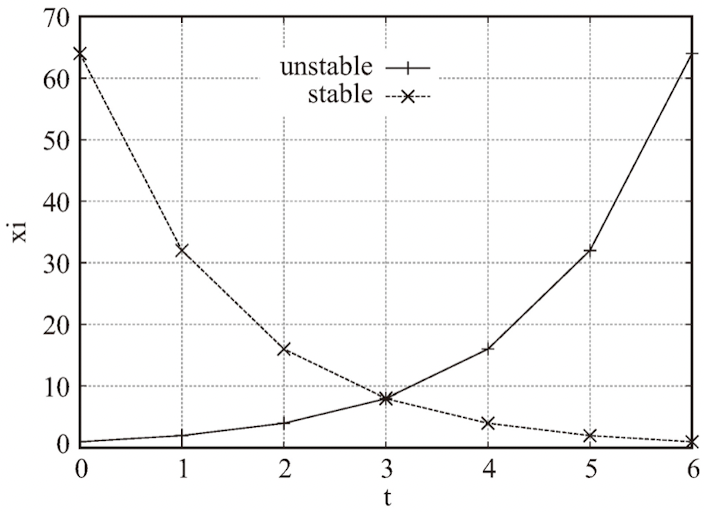
  '폭주의 위험이 있는가' 즉 어떠한 상황에서 시작해도 $ℰ(t)$는 유한한 범위에 머무르는가(폭주하지 않음), 아니면 운이 나쁜 상태에서 시작하면 $|ℰ(t)|$가 무한대로 커져 버리는가(폭주)를 판정한다.
  

• 폭주를 하지 않는 시스템의 전형적인 예 : $ℰ(t)$ = $0.5ℰ(t-1)$

• 폭주를 하는 시스템의 전형적인 예 : $ℰ(t)$ = $2ℰ(t-1)$

• 4.2) 1차원의 경우

  • 우선 쉬운 경우를 생각한다.

  • 일반적인 경우도 어떻게든 변환하여 쉬운 경우로 귀착시킨다.

  • $x(t) = ax(t-1)$

    • $|a| > 1$이면 폭주, $|a| < 1$이면 폭주하지 않는다.

• 4.3) 대각행렬의 경우

  $x(t) =$ $\begin{pmatrix}5&0&0\\0&-3&0\\0&0&0.8\\ \end{pmatrix}$$x(t-1)$ $\to$$\begin{pmatrix}x_1(t)\\x_2(t)\\x_3(t)\\ \end{pmatrix}$$=$ $\begin{pmatrix}5x_1(t-1)\\-3x_2(t-1)\\0.8x_3(t-1)\\ \end{pmatrix}$
  즉,
  $\begin{aligned} x_1(t)&=5x_1(t-1)\\ x_2(t)&=-3x_2(t-1)\\ x_3(t)&=0.8x_3(t-1) \end{aligned}$

  $\begin{aligned} x_1(t)&=5x_1^t(0)\\ x_2(t)&=-3x_2^t(0)\\ x_3(t)&=0.8x_3^t(0) \end{aligned}$

행렬이 대각행렬일 때
$x(t) = Ax(t-1)$
$A = diag(a_1,...a_n)$
$x(t) = (x_1(t),...,x_n(t))^T$
이면 Ax는 단지 $(a_1x_1,...,a_nx_n)^T$이므로
$x_1(t) = a_1x_1(t-1), .... ,x_n(t) = a_nx_n(t-1)$

즉,

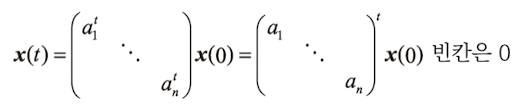
$|a_1|,...,|a_n|$ 중 하나라도 1보다 크면 폭주합니다.
$|a_1|,...,|a_n| \leq 1$이면 폭주하지 않습니다.

• 4.4) 대각화 할 수 있는 경우

  A가 대각행렬이라면 해결이지만 아닌경우는 A를 대각행렬로 귀착한다.
  

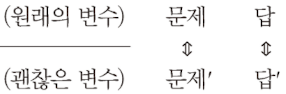
'좋은 정칙행렬 $P$를 골라 $P^{-1}AP$를 대각행렬로 한다' : '대각화'

• 4.4.2) 좋은 변환을 구하는 방법

  • $P^{-1}AP = Λ = diag(\lambda_1,...,\lambda_n)$
  • $AP = PΛ$ , $(Ap_1,...,Ap_n) = (\lambda_1p_1,...,\lambda_np_n)$
  • 일반적으로 정방행렬 A에 대해
    • $Ap_1 = \lambda_1p_1$
    • $p ≠ 0$
    • 이를 만족시키는 수 $\lambda$, 벡터 $p$를 각각 '고유값','고유벡터'라고 한다.

• 4.4.4) 거듭제곱으로서의 해석

  • $x(t) = Ax(t-1) = AAx(t-2) = A^tx(0)$
  • $(P^{-1}AP)^t = P^{-1}A^tP$
  • $(P^{-1}AP)^t = Λ^t$
  • $PΛ^tP^{-1} = A^t$
  • $x(t) = PΛ^tP^{-1}x(0)$

• 4.5) 결론 : 고유값의 절댓값 나름

  대각화 할 수 있는 경우의 결론은 다음과 같다.

  • $|\lambda_1|,...,|\lambda_n|$ 중 하나라도 1보다 크면 '폭주 위험이 있음'
  • $|\lambda_1|,...,|\lambda_n| \leq 1$이면 '폭주 위험이 없음'

---