2장) 랭크ㆍ역행렬ㆍ일차방정식
-
2.4) 성질이 좋고 나쁨의 판정(역행렬이 존재하기 위한 조건)
y=Ax에서 A가 정사각이 아니라면 해의 존재성이나 일의성, 어느 쪽인가가 무너진다.
그렇기에 이 절에서는 A가 정방행렬인 경우로 이야기를 한정 -
2.4.1) 성질이 좋고 나쁨의 판정(역행렬이 존재하기 위한 조건)
'납작하게 눌리는가'가 포인트
- 납작하게 눌린다면 역행렬 없음
- 납작하게 눌리지 않으면 역행렬 있음
-
2.4.2) 정칙성과 같은 조건 여러 가지
동치인 것
- A의 사상은 '납작하게 눌리지 않는다.'
- A의 사상은 단사
- Ker A가 원점 o뿐
- dim Ker A = 0
동치인 것
- A의 사상은 '목적지 공간 전체를 커버한다.'
- A의 사상은 전사
- Im A가 n차원 공간 전체
- rank A = dim Im A = n
-
2.4.3) 정칙성의 정리
n차 정방행렬 A = (a₁,...a𝒏)에 대해 다음 내용은 모두 같다.
- 어떤 n차원 벡터 y에도 y = Ax가 되는 x가 딱 한 개 있다.
- A는 정칙행렬(역행렬 A⁻¹이 존재)
- A의 사상은 '납작하게 눌리지 않는다' (단사)
- Ax = o이 되는 것은 x = o뿐 (Ker A가 원점 o뿐, dim Ker A = 0)
- A의 열벡터 a₁,...,a𝒏이 선형독립
- A의 사상은 '목적지 공간 전체를 커버한다.' (A의 사상은 전사, Im A가 n차원 공간 전체)
- rank A = dim Im A = n
- det A ≠ 0
- A가 고유값 0을 지니지 않는다.
- 이상의 A를 Aᵀ로 치환한 것
-
2.5) 성질이 나쁜 경우의 대책
-
2.5.1) 구할 수 있는 데까지 구한다 (1) 이론편
성질이 나쁜 행렬 A에서는 Ax = y의 해가 없거나 많다.
- 해는 존재하는가?
- 행렬 A가 특이행렬일 경우에도 해는 존재할 수 있다.
- 해를 모두 찾자
- 하나의 해인 x₀에 Ker A에 속하는 임의의 벡터 z를 가져와서 해를 만든다.
- 정칙행렬의 경우 Ker A가 원점이므로 하나의 해만 나온다.
- 정리
- 해를 하나 발견한다. 이 해 x₀를 특해라고 한다.
- 원래 방정식의 우변을 0으로 한 Az = 0(동차방정식)의 모든 해(일반해)를 구합니다.
- Ax = y의 해는 '(특해) + (동차방정식의 일반해)'로도 얻어집니다.
- 해는 존재하는가?
-
2.5.2) 구할 수 있는 데까지 구한다 (2) 실전편
성질이 나쁜 경우
- 단서가 너무 많은 전형적인 예(해 없음)
- 단서가 부족한 전형적인 예(해가 많음)
-
2.6) 현실적으로는 성질이 나쁜 경우(특이에 가까운 행렬)
노이즈가 있는 공학의 세계에서는 특이에 아주 가까운 정칙행렬이란 대부분 특이행렬과 같다.
- A가 '매우 압축된'행렬이라면
- 그것을 원래 상태로 돌려 놓는 A⁻¹은 '매우 확대하는'행렬이 되어
- 그러면 노이즈도 매우 확대된다.
-
2.6.2) 대책 예 : 티호노프의 정칙화
A가 정칙인 경우에는 보통 구한 해가 x = A⁻¹y와 같은 결과가 되기 떄문에 도움이 되지 않음(노이즈의 경우)
이 때 자주 이용하는 방법은 다음과 같습니다.- Ax와 y의 '차이'를 측정한다.
- x 자체의 '그럴듯함'을 측정한다. 또는 같은 것이지만, x의 '부자연스러움'을 측정한다.
- '차이'와 '부자연스러움'의 한계치가 최소가 되는 x를 답한다.
실제로는 다음과 같은 방법을 자주 사용한다. - Ax - y의 '길이' ||Ax-y||를 이용하여 '차이'를 잰다.
- x의 '길이' ||x||를 이용하여 '부자연스러움'을 잰다.
- ɑ를 무언가로 설정하여 ||Ax-y||² + ɑ||x||²이 최소가 되는 x를 구한다.
3장) 컴퓨터에서의 계산 (1)
컴퓨터로 구체적인 수치를 계산할 때는 다음과 같은 사항을 신경 쓰지 않으면 안된다.
- 수치의 정도(정밀도)는 유한하다.
- 계산량ㆍ메모리 소비량을 줄이고 싶다.
3.3) LU 분해
주어진 행렬 A에 대해 A를 하삼각행렬 L과 상삼각행렬 U의 곲으로 나타내는 것을 LU분해라고 한다.
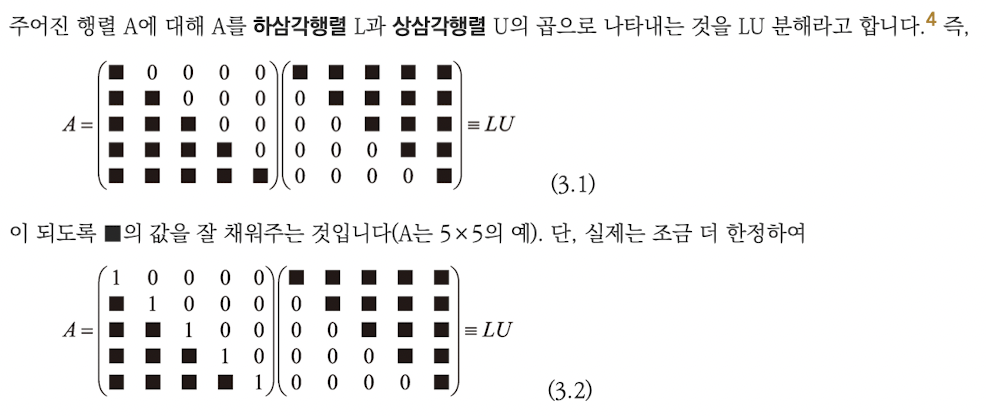이를 분해하면 '적은 계산량으로' 행렬식을 구하거나 일차 방정식을 풀 수 있다.3.5) 행렬식을 LU 분해로 구하다.
det A = det(LU) = (det L)(det U)
이 때 하삼각행렬이나 상삼각행렬의 행렬식은 대각성분의 곱이다.
즉 det L은 1이기에 det A = U의 대각성분의 곱3.6) 일차방정식을 LU 분해로 풀다.
정칙인 n차 정방행렬 A와 n차원 벡터 y에 대해 Ax = y가 되는 x를 구하는 문제
A = LU라고 분해되어 있다면 LUx = y의 의미는 'x를 우선 U에 곱하고, 거기에 L을 곱하면 y가 된다.'
Ax = LUx = L(Ux) = y- 하삼각행렬(z)
* 상삼각행렬(x 구하기)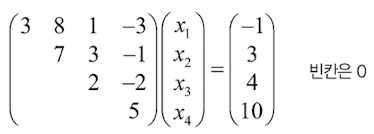 
- 하삼각행렬(z)
3.7) 역행렬을 LU 분해로 구하다.
A의 역행렬을 X로 둔다. 이에 Ax₁ = e₁,...,Ax𝒏 = e𝒏
'A를 곱하면 ...이 되는 벡터를 구하라'는 3.6에서 푼 문제이다. 즉 A를 LU 분해를 하면 다양한 곳에 재사용이 가능하다.
많은 응용에서 A⁻¹자체가 아닌 '어느 벡터 y에 대한 A⁻¹y'를 얻으면 충분하다. 그런 때는 'A⁻¹을 구하여 y에 곱'하는 것보다 '연립일차방정식 Ax = y를 푼다'가 계산량 및 정도(오차의 축적)의 관점에서 유리하다.3.8) LU 분해의 순서(2) 예외가 발생한 경우
- 정렬이 필요한 상황
- 행렬 A(k)의 (1,1)성분 a₁₁(k)가 0이되면 1/a₁₁(k)를 계산할 수 없다. 이 경우 피보팅이라는 수단을 사용한다.
- 이 경우 치환행렬을 사용한다. 치환행렬이란 '어느 행에도 1이 하나씩' 또는 '어느 열에도 1이 하나씩'(나머지는 0)이란 이런 정방행렬
- 정렬해도 앞이 막혀버리는 상황
이 경우 열의 교체까지 허용한다.- 행렬식 det A에 대해서는 만약 도중에 막히면 det A = 0
- 연립일차방정식 Ax = y에 대해서는 만약 도중에 막히면 '성질이 나쁜 경우'
- 정렬이 필요한 상황
