2장) 랭크ㆍ역행렬ㆍ일차방정식
-
2.1) 문제 설정 : 역문제
결과 y를 알고, 원인 x를 추정하는 형태의 문제
노이즈도 고려해야한다. -
2.2) 성질이 좋은 경우(정칙 행렬)
x,y의 차원이 같다면 A는 정방행렬이고 이 때 A의 역행렬이 존재한다면 식은
x = A⁻¹y이며 이것으로 결과 y에서 원인 x를 알 수 있다.
즉 역행렬이 존재하는 정방행렬 A를 정칙행렬이라고 한다.
정칙이 아닐경우 특이행렬 -
2.3) 성질이 나쁜 경우
- 단서가 부족한 경우
y가 x보다 차원이 작은 경우 ex)y:2차원,x:3차원
이 경우 원래보다 차원이 낮은 공간으로 옮기는 것 - Kernel(핵)
주어진 A에 의해 Ax = 0으로 이동해 오는 것과 같은 x의 집합을 A의 핵(kernel)이라고 하며, Ker A라고 나타낸다. Ker A는 '사상 A에서 납작하게 눌러지는 방향'을 나타낸다.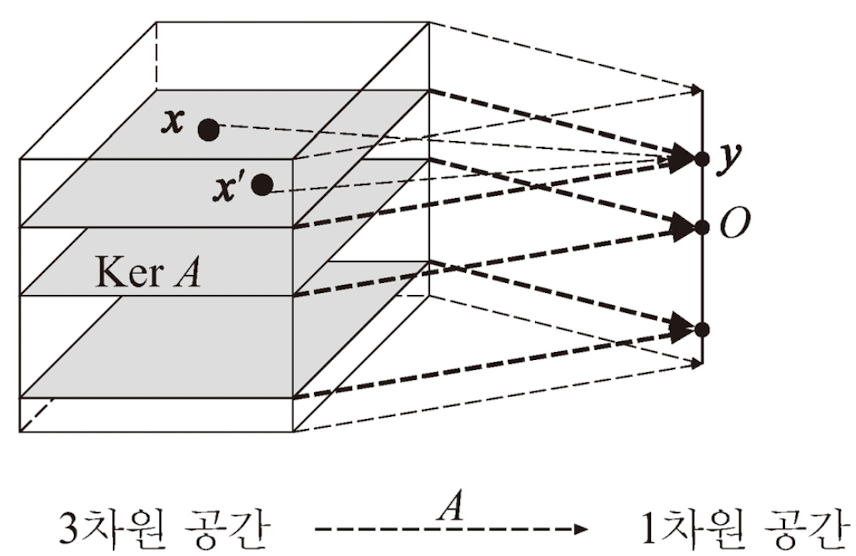
- 단서가 너무 많은 경우
원래보다 높은 차원으로 옮기는 경우 높은 차원의 모든 공간을 커버하는 것이 불가능하다. 그렇기에 주어진 A에 대해 x를 여러모로 움직인 경우에 A로 옮기는 y = Ax의 집합을 A의 상(image)이라고 하며, Im A라 나타낸다.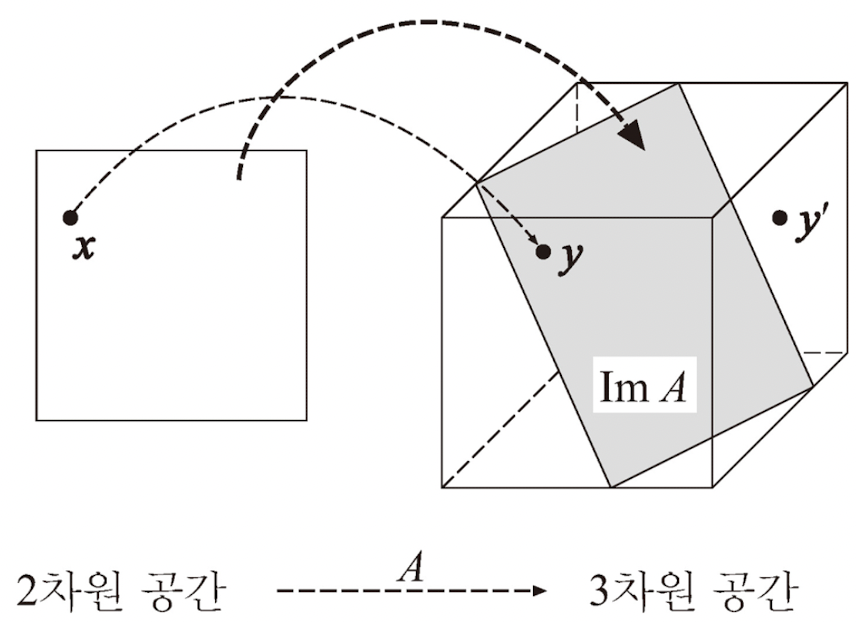
- 특이행렬의 경우 단서의 개수가 일치해도 공간이 '납작하게 눌린다.'그렇기에 '단서가 부족한 경우'와 마찬가지로 y를 봐도 x의 후보가 유니크하게 결정되지 않는다. 또한 납작하기에 y의 공간 전체를 커버할 수 없다. '단서가 너무 많은 경우'와 같이 y에 거기로 이동해온 x가 존재하지 않을 수 있다(노이즈로 인해).
- 단서가 부족한 경우
-
2.3.2) 성질의 나쁨과 핵ㆍ상
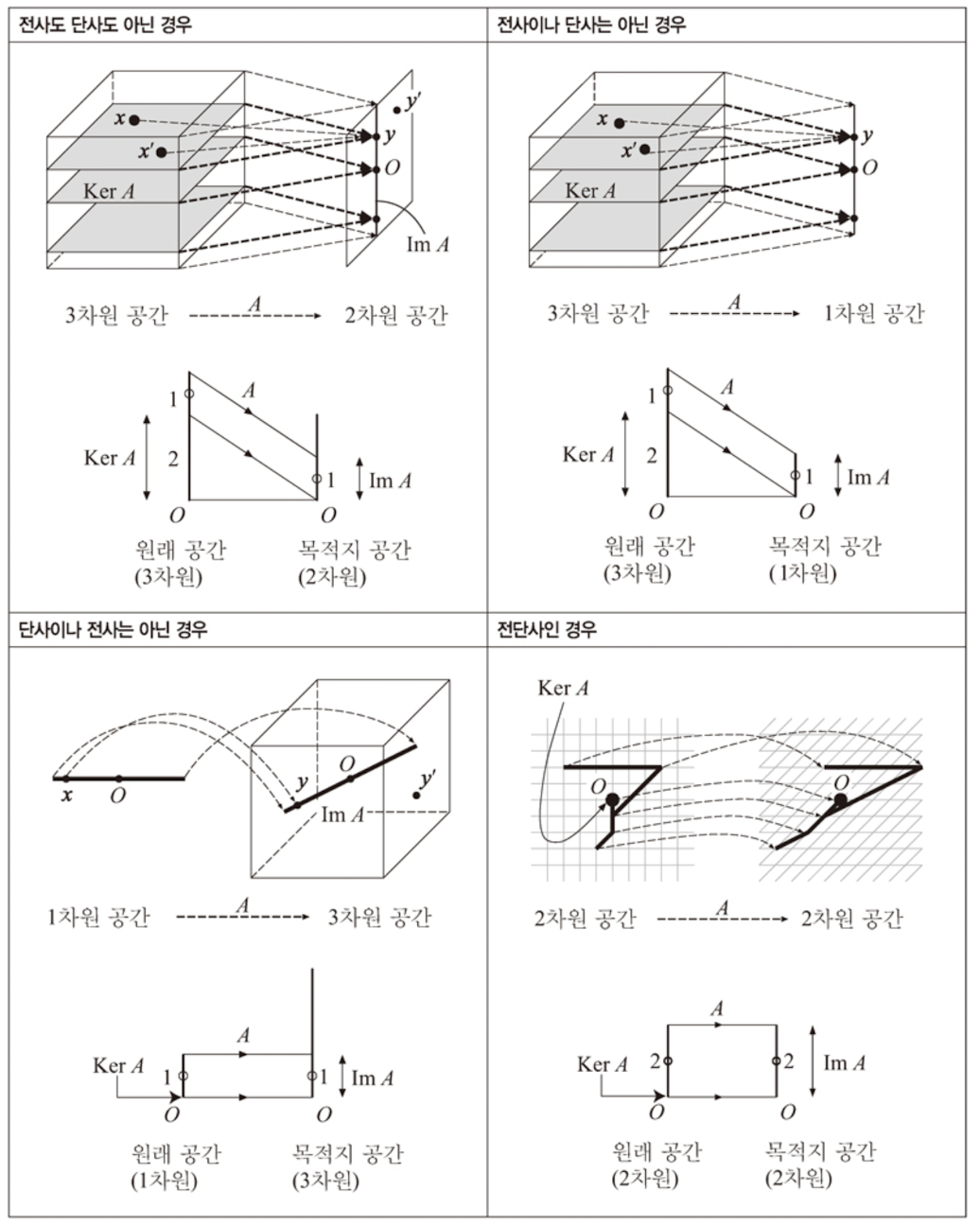
- 같은 결과 y가 나오는 원인 x는 유일한가 (y = Ax는 단사)
- 어떤 결과 y에도 그것이 나오는 원인 x가 존재하는가 (y = Ax는 전사)
- 양자가 성립하는 경우 '사상 y=Ax는 전단사'
Ker A와 Im A라는 개념을 사용하여 기술
- Ker A가 '원점 0뿐' (사상은 단사)
- Im A가 '목적지의 전 공간'(치역)에 일치 (사상은 전사)
- 이것이 '연립일차방적식의 해의 존재성과 일의성'에 대한 답
-
2.3.3) 차원 정리
m x n 행렬 A에 대해
- dim Ker A + dim Im A = n
- n - dim Ker A = dim Im A
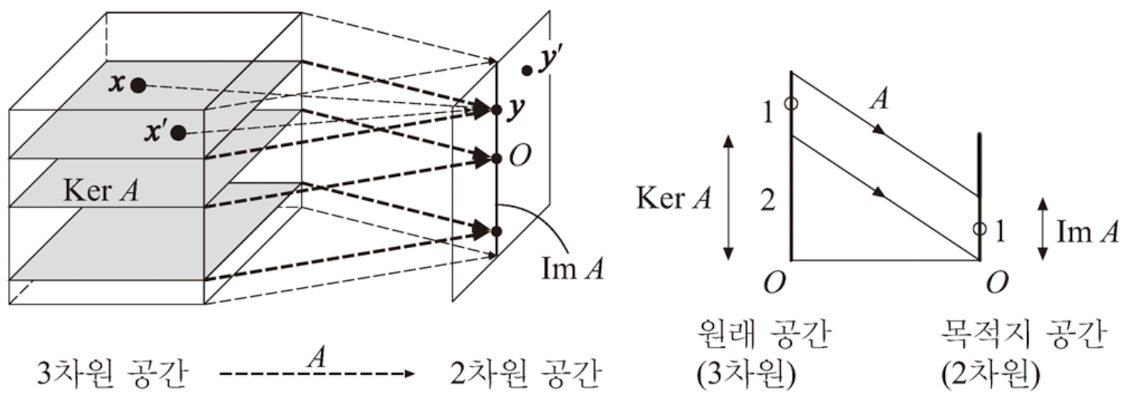A는 n차원 공간에서 m차원 공간으로의 사상 '원래의 n차원 공간에서 Ker A의 차원 부분이 눌리고 남은 것이 Im A의 차원 부분' - m < n이면 단사는 될 수 없다.
(Im A는 목적지 m차원 공간의 일부이므로 dim Im A ≤ m. 여기서 m < n이 되면 dim Im A < n이 되어 차원 정리에 따라 dim Ker A > 0) - m > n이면 전사는 될 수 없다.
('차원'은 0 이상이므로 Ker A에 대해서도 dim Ker A ≥ 0. 그러므로 차원 정리에 따라 dim Im A ≤ n. 여기서 m > n이 되면 dim Im A < m이 됩니다.)
-
2.3.4) '납작하게'를 식으로 나타내다(선형독립,선형종속)
'납작하게 눌린다'를 쉽게 표현하면 '서로 다른 x와 xʹ가 같은 y로 이동한다.'
- 선형종속 : x ≠ xʹ일 때 성립하는 x = (x₁,...,x𝗇)ᵀ와 xʹ = (xʹ₁,...,xʹ𝗇)ᵀ가 존재한다
- 선형종속이 아닌 경우 a₁,...,a𝗇은 선형독립
- A의 열벡터들이 선형종속 = 납작하게 눌린다.
- A의 열벡터들이 선형독립 = 납작하게 눌리지 않는다.
즉 수 u₁,...,u𝗇에 대해 u₁a₁ + ... + u𝗇a𝗇 = 0이라면
'u₁ = ... = u𝗇 = 0'이라는 조건이 성립할 때
벡터 a₁,...,a𝗇은 선형독립이라고 할 수 있다.
a₁,...,a𝗇이 선형종속이면 A에 의한 사상도 '납작하게 누르는 사상이 된다.' - '다른 열을 몇 배하여 모두 더한다'라는 형태로 쓰이는 것이 '납작하게 눌리는' 행렬의 특징
-
2.3.5) 단서의 실질적인 개수(랭크)
앞서 '납작하게 눌리는가'를 검토했다면 다음은 '이동점의 공간 전체를 커버할 수 있는가'를 검토
즉 '상 Im A가 공간 전체를 커버하고 있는가' 이를 체크하기 위해서는 Im A의 차원에 주목- 랭크의 정의 : A를 m x n 행렬이라고 가정, 여기서 상 Im A의 차원 dim Im A에는 '행렬 A의 랭크(rank)'라는 이름이 붙어있다. 기호로는 rank A
- 이 기호를 사용하여 차원 정리를 하면
dim Ker A + rank A = n
즉 rank A를 아는 것과 Ker A의 차원을 아는 것은 거의 같다. - 랭크와 핵, 상과 단사, 전사
- Ker A가 원점 o뿐인가? (그렇지 않으면 y = Ax에서 같은 y로 이동하는 x가 여러개 존재)
- Im A가 m차원 공간 전체를 커버하는가? (그렇지 않으면 삐져나온 y에는 y=Ax에서 이동해오는 x가 없다.)
이는 각각 - Ker A는 0차원인가? : rank A = n (단사)
- Im A는 m차원인가? : rank A = m (전사)
- 랭크의 기본 성질
rank A ≤ m, rank A ≤ n
정칙행렬을 곱해도 랭크는 변하지 않는다. (정칙행렬은 '납작하게 누르지 않는' 변환이기에)
rank(PA) = rank A, rank(AQ) = rank A
일반행렬 B,A에 대하여
rank(BA) ≤ rank A, rank(BA) ≤ rank B - 보틀넥 형의 분해
A의 랭크 r에 대응하는 형태로 A를 '날씬한 행렬의 곱'으로 분해할 수 있다.
폭이 r인 행렬 B와 높이가 r인 행렬 C로
A = BC
AI 새싹