프로그래머를 위한 선형대수(1)

0장) 왜 선형대수를 배워야 하는가?

• 0.1) 공간이라고 생각하면 직관이 먹힌다.

  벡터 공간은 현실 공간의 성질을 특정 수준에서 추상화 한 것.
  따라서 선형대수는 공간을 설명하는 데 편리한 용어나 개념을 제공해줌

• 0.2) 근사 수단으로 사용하기 편리하다.

  대상의 대부분이 줌업하면 거의 다 곧기에 선형대수를 적용할 수 있다.

1장) 벡터ㆍ행렬ㆍ행렬식

많은 수치를 묶은 데이터를 '수치의 조합'이 아닌 '공간 안의 점'으로 간주하는 직관을 활용하자
'공간'이라는 직관을 잊지 말자!

	문자 배열(표면상)	의미
벡터	숫자를 일렬로 늘어 놓은 것	화살표,또는 공간 안의 점
행렬	숫자를 직사각형으로 늘어 놓은 것	공간에서 공간으로의 직교 사상
행렬식	뭔가 귀찮은 계산	위의 사상에 따른 부피 확대율

• 1.1) 벡터와 공간

  • 수치의 조합을 정리하여 나타내는 기법
    수를 나열한 것을 벡터라고 부른다.
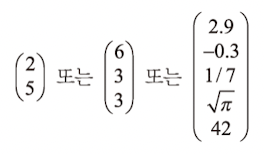    '종벡터' : 세로로 늘어선 벡터(일반적)
    '횡벡터' : 가로로 늘어선 벡터

• 1.1.2) '공간'의 이미지

  • 벡터를 공간 안 어디간에 한 점으로 나타낼 수 있다.
    이런 식으로 위치에 대응시키는 것을 강조할 때는 '위치 벡터'라고 부르기도 한다.

• 1.1.3) 기저

  • 원점과 '화살표 해석'으로 덧셈, 정수배가 정의된 세계를 선형 공간 혹은 벡터 공간이라고 한다.
  • 특정 벡터의 좌표를 매기기 위해 기준이 필요하다. 이 때 사용되는 기준이 기저 벡터

• 1.1.4) 기저가 되기 위한 조건

1. 공간안의 어떤 벡터라도 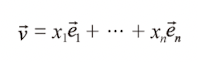라는 형태로 나타낼 수 있다.
2. 하나의 벡터를 나타내는 방법은 하나이다.

• 1.1.5) 차원

  • 차원 = 기저 벡터의 개수 = 좌표의 성분 수
    기저 벡터의 개수로 그 공간의 차원을 정의함

• 1.1.6) 좌표에서의 표현

  • "3776m"에서 값 '3776'이 좌표, 단위 'm'가 기저

• 1.2) 행렬과 사상

  • 수를 직사각형 형태로 나열한 것을 행렬이라고 부른다.
  • 행 수와 열 수가 같은 행렬을 '정방행렬'이라고 부른다.
  • 일반적으로 행렬은 알파벳 대문자, 성분은 소문자로 쓴다.
  • 행렬과 벡터의 곱은 벡터
  • 행렬의 열 수가 '입력'의 차원 수, 행 수가 '출력의 차원 수

• 1.2.3) 행렬은 사상이다.

  • 행렬 A를 지정하면 벡터를 다른 벡터에 옮기는 사상이 결정된다. 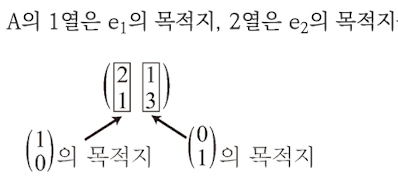기저 벡터가 변하면서 공간이 변한다.
  • '사상이 같다면 행렬도 같다.'
    Ax = Bx -> A = B

• 1.2.4) 행렬의 곱 = 사상의 합성

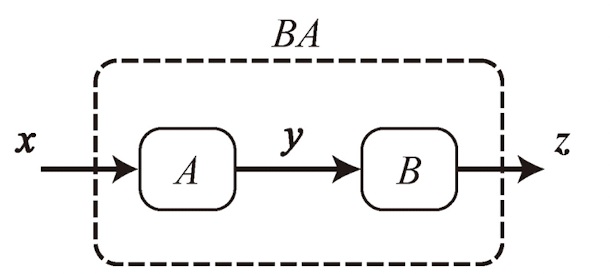
  • (BA)x = B(Ax) = BAx
  • y = Ax, z = B(Ax) = By

• 1.2.6) 행렬의 거듭제곱 = 사상의 반복

• 1.2.7) 영행렬, 단위행렬, 대각행렬

  • 영행렬 : 모든 성분이 0인 행렬
  • A ≠ 0, A² = 0 가능
  • A ≠ 0, B ≠ 0, BA = 0 가능
  • 단위행렬 : 정방행렬에서 '\'방향의 대각선 위만 1이고 다른 것은 모두 0인 행렬
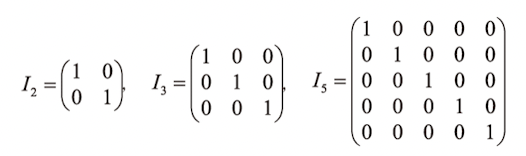
    단위행렬이 나타내는 사상은 '아무것도 하지 않는' 사상
  • 대각행렬 : 정방행렬의 '\'방향의 대각선상의 값을 대각성분
    대각성분 이외의 값은 비대각성분
    이 때 비대각성분이 모두 0인 행렬을 대각행렬
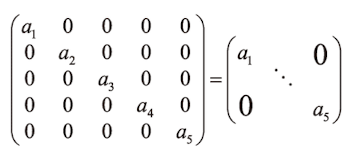
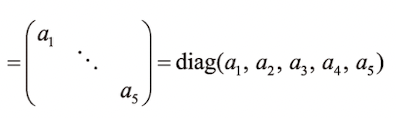    대각 행렬이 나타내는 사상은 '축에 따르는 신축', 대각 성분이 각 축의 늘고 주는 배율이 된다.

• 1.2.8) 역행렬 = 역사상

  • 정방행렬 A에 대해 그 역사상에 대응하는 행렬을 'A의 역행렬', A⁻¹
  • 역행렬은 없을 수도 있다. 납작하게 눌리는 즉 detA가 0인경우는 없다.
  • 대각행렬의 경우 '축에 따른 신축'이기에 1/a𝑛으로 변경해주면 역행렬 하지만 a₁...a𝑛에 0이 있으면 역행렬은 존재하지 않는다.

• 1.2.9) 블록행렬

  • 큰 문제를 작은 부분 문제로 분할하는 것
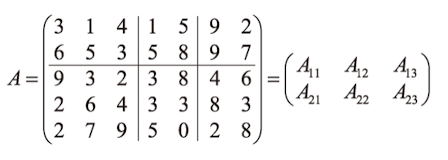
  • 행벡터, 열벡터
    열벡터가 각 축 방향의 단위벡터의 목적지다.

• 1.2.11) 좌표 변환과 행렬

  • 어떻게 기저를 취하여 좌표를 표현해도 실체로서의 벡터 자체는 같다.
    주어진 문제에 따라 적절한 기저를 취한다.
    이를 통해 손쉽게 답을 구하고 원래의 기저에 돌려주면 원하는 답을 얻을 수 있다.

• 1.2.12) 전치행렬

  • 행렬 A의 행과 열을 바꿔넣는 것을 A의 전치행렬이라고 하며 Aᵀ라고 쓴다.

• 1.3) 행렬식과 확대율

• 1.3.1) 행렬식 = 부피 확대율

  • det A or |A|

• 1.3.2) 행렬식의 성질

  • det A⁻¹ = 1 / A⁻¹
  • det A = 0이면 A⁻¹은 존재하지 않는다.
  • det(diag(a₁...a𝑛)) = a₁...a𝑛
    대각행렬 diag(a₁...a𝑛)이 나타내는 사상이 축 방향으로 a𝑛배이기 때문
  • 어느 열이든 두 열이 완전히 같은 경우에는 한 번에 det A = 0이 됩니다.
  • 행렬식은 '어느 열의 정수배를 다른 열에 더해도 값이 변하지 않는다'라는 성질이 있습니다.
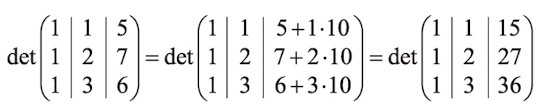
  • 대각성분보다 아래 쪽이 모두 0인 행렬을 '상삼각행렬'이라고 합니다.
    
  • 전치행렬의 행렬식은 원래 행렬의 행렬식과 같습니다.