4장) 고유값, 대각화, 요르단 표준형(폭주의 위험이 있는지)
-
4.5) 고유값, 고유벡터
앞에서 설명한 바와 같이 폭주 위험을 판정하기 위한 열쇠는 고윳값과 고유벡터이다.
일반적으로 정방행렬 A에 대해 다음을 만족하는 수 와 벡터 를 '고유값', '고유벡터'라고 한다.
-
4.5.1) 기하학적인 의미
고유벡터의 기하학적인 의미는 'A를 곱해도 신축만 되고, 방향은 변하지 않는다.'이며
이 때 신축률(몇 배가 되는가)이 고윳값입니다. -
4.5.2) 고윳값, 고유벡터의 성질
한눈에 들어오는 성질
- A가 고윳값 0을 지니는 것과 A가 특이인 것은 동치다. 즉, A가 고윳값 0을 지니지 않는 것과 A가 정칙인 것은 동치다.
- 나 도 A의 고유벡터다. 일반적으로 에 대해 는 A의 고유벡터이다.
- 같은 고윳값 의 고유벡터 를 가져오면 도 A의 고유벡터(고윳값 )다. 단, 인 경우는 제외한다.
- 는 나 의 고유벡터이기도 하다.(고윳값은 각각 , ). 일반적으로 는 의 고유벡터이기도 하다.(고윳값은 )
- 는 나 의 고유벡터이기도 하다(고윳값은 각각 ). 일반적으로는 의 고유벡터이기도 하다(고윳값은 ).
- 는 이나 의 고유벡터이기도 하다(고윳값은 각각 ). 일반적으로 k = 1, 2, 3,...에 대해 는 의 고유벡터이기도 하다(고윳값은 )
- 는 의 고유벡터이기도 하다.(이 존재할 때). 고윳값은 .
- 대각행렬 의 고윳값은 5, 3, 8이다. 가 대응하는 고유벡터이다. 일반적으로 대각행렬 의 고유값은 이 대응하는 고유벡터(는 i성분만이 1이고, 나머지는 0인 n차원 벡터)다.
- 블록대각행렬의 고윳값, 고유벡터는 대각블록별로 생각하면 된다.
- 상삼각행렬이나 하삼각행렬의 고윳값은 대각성분 그 자체다
- A와 같은 크기의 정칙행렬 S에 대해 는 의 고유벡터(고윳값 )이다. 따라서 A와 는 같은 고윳값을 지닌다. '닮음변환으로 고윳값은 변하지 않는다.'
- 행렬식은 고윳값의 곱이다. 즉 n x n 행렬 A의 고윳값이 인 경우 det A =
- 대각화를 할 수 있는 경우
고유벡터의 선형독립성
다른 고윳값에 대응하는 고유벡터는 선형독립이다.
-
가 n x n 행렬 A의 고윳값이고, 가 대응하는 고유벡터라고 한다. 만약 가 모두 다르면 는 선형독립이다.
-
n x n행렬 A가 n개의 서로 다른 고윳값 을 지니면 대응하는 고유벡터 을 나열한 행렬 P = 은 정칙이고, 으로 대각화할 수 있다.
-
4.5.3) 고윳값의 계산 : 특성방정식
벡터 가 n x n 행렬 A의 교유벡터다.(고유값은 )의 의미는 다음과 같다.
이 아닌 벡터 에 행렬 를 곱하면 이 되어 버린,
즉 행렬 가 '납작하게 누르는' 특이행렬이 된 것입니다. 그런 특이행렬의 행렬식은 0이 됩니다.
반대로 이면 는 특이행렬이고,
그런 경우 이 아닌데 를 곱하면 이 되어버리는 벡터가 존재한다.
이러한 이유로 가 의 고윳값인 것과
가 0이 되는 것은 동치입니다.
를 특성다항식(고유다항식)이라 부르고,
의 방정식 을 특성방정식(고유방정식)이라고 합니다.
실제로 는 변수 의 n차 다항식이 되는 것이 행렬식의 계산법의 식에서 보증됩니다.
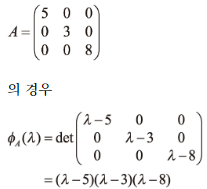 의 해는 = 5,3,8
의 해는 = 5,3,8
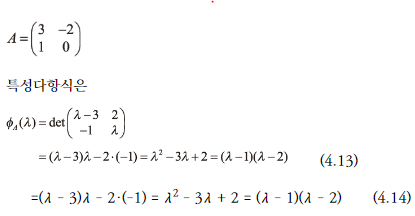 해당 A의 고윳값은 1,2이다.
해당 A의 고윳값은 1,2이다.
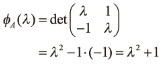 다음과 같이 실행렬 A에서 고윳값,고유벡터가 복소수인 경우가 있다.
다음과 같이 실행렬 A에서 고윳값,고유벡터가 복소수인 경우가 있다.
-
4.5.4) 고유벡터의 계산
행렬 A의 고윳값 이 구해지면 남은 것은 고유벡터 를 찾는 것입니다.
앞서 본 행렬 A = 의 고윳값은 입니다. 고유벡터 로 두고 를 만족시키는 를 찾아봅시다.-
인 경우
- 고유벡터 =
-
인 경우
- 고유벡터 =
-
중복고윳값(성질이 좋은 경우)
상삼각행렬의 고윳값은 대각성분 그 자체이다.
그러므로 A의 고윳값은 3(이중해)와 2이다.- 고윳값 2에 대응하는 고유벡터
-
