데이터베이스를 설계할 때 불필요한 중복 등으로 인하여 이상 현상(Anomaly)이 발생할 수 있다. 그리고 이 이상현상을 제거하기 위하여 데이터를 여러 릴레이션으로 분해하는 과정을 정규화(Normalization)라 한다. 정규화를 통해 테이블을 여러 개로 분할하면 상대적으로 속도가 느려질 수 있지만, 정규화를 하지 않으면 이상 현상이 발생할 수 있다.
이상 현상(Anomaly)
이상 현상이란 데이터베이스 내의 데이터들이 불필요하게 중복되어 데이터를 삽입, 삭제, 수정할 때 논리적으로 발생하는 오류를 말한다. 크게 삽입 이상(Insertion anomaly), 삭제 이상(Deletion anomaly), 갱신 이상(Update anomaly)의 셋으로 구분한다.
각 이상 현상을 다음의 예시를 바탕으로 살펴보자.
| 학번 | 이름 | 나이 | 성별 | 강의 코드 | 강의명 | 전화번호 |
|---|---|---|---|---|---|---|
| 1001 | 홍길동 | 21 | 남 | AC01 | 국어학개론 | 01X-1234-5678 |
| 1002 | 정미나 | 24 | 여 | AC03 | 현대문학사 | 01X-4321-8765 |
| 1003 | 김으뜸 | 22 | 남 | AC02 | 국어음운론 | 01X-9876-5432 |
| 1004 | 박규 | 20 | 남 | AC04 | 소설창작 | 01X-6789-2345 |
| 1002 | 정미나 | 24 | 여 | AC06 | 음운론 | 01X-4321-8765 |
| 1005 | 구은혜 | 23 | 여 | AC05 | 고전문학사 | 01X-1928-3746 |
삽입 이상(Insertion anomaly)
삽입 이상은 테이블에 데이터를 삽입할 때 의도와 상관 없이 원하지 않은 데이터까지 삽입해야 테이블에 데이터 추가가 가능한 현상을 말한다.
상기 예에서 아무런 강의룰 수강하지 않은 새로운 학생을 추가하려면 강의 코드와 강의명에는 null값이 들어가게 되는 문제가 발생한다.
삭제 이상(Deletion anomaly)
삭제 이상은 어떤 데이터를 삭제하고자 할 때 의도하지 않은 다른 데이터까지 삭제되는 현상을 말한다.
상기 예에서 강의 코드가 AC03인 '현대문학사' 강의가 폐강되어 삭제하고자 할 경우, 해당 과목을 수강한 '정미나' 학생의 데이터까지 모두 삭제되는 문제가 발생한다.
갱신 이상(Update anomaly)
갱신 이상은 중복된 데이터 중 일부만 수정되어 모순이 일어나는 현상을 말한다.
상기 예에서 강의 코드가 AC03인 '정미나' 학생의 전화번호를 수정할 경우, 두 번째 인스턴스의 데이터만 수정될 것이다. 이 경우 5번째 인스턴스 역시 동일한 사용자임에도 불구하고 전화번호가 달라지는 문제가 발생한다.
정규화(Normalization)
데이터 정규화(Normalization)는 크게 두 가지 목적을 가지고 실시된다. 첫 번째는 불필요한 데이터(중복 데이터 등)를 제거함으로써 데이터를 효율적으로 활용하는 것이고, 두 번째는 상기에서 설명한 이상 현상을 방지하는 것이다.
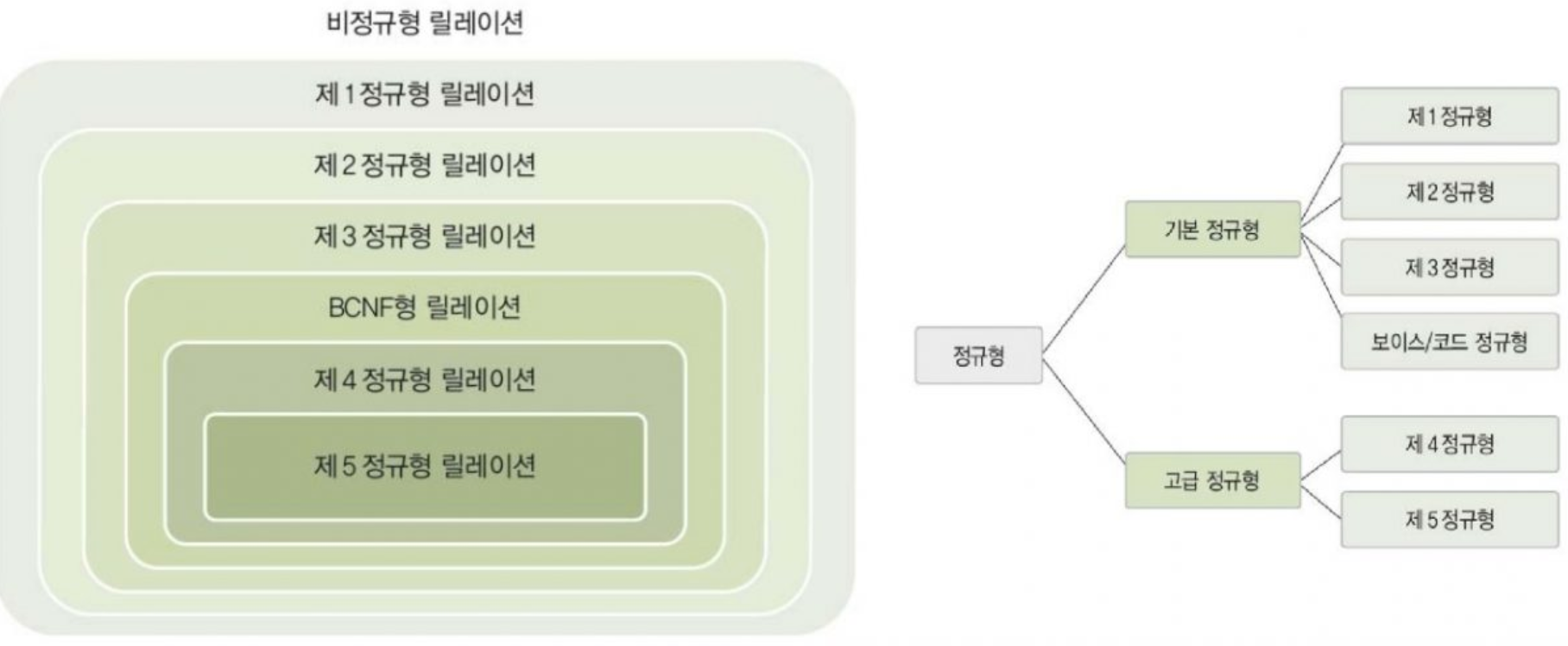
정규화는 제1정규화부터 제6정규화까지 존재하지만, 일반적으로는 제1정규화부터 제3정규화까지의 과정을 거치게 된다.
함수 종속성(Functional Dependency)
정규화 시에는 함수 종속성을 판단하여 진행하는데, 이때 함수 종속성이란 각 속성들 간의 관련성을 의미한다. 어떤 릴레이션 R의 속성(attribute) 중 속성 X와 Y가 존재할 때, X의 값에 따라 Y의 값이 결정된다면 Y는 X에 대해 함수 종속이라 하며 X → Y로 표기한다. 그리고 이때 X를 결정자(Determinant set), Y를 종속자(Dependent set)라 한다.
예를 들어 보자. 어떤 차량과 배기량을 기록한다고 하면 각 차량에는 차량별로 고유한 차량 식별 번호(ID)를 부여할 것이다. 그렇다면 'ID → 배기량'으로 적을 수 있다. 각 차량은 하나의 배기량만을 갖기 때문이다. 그러나 거꾸로 '배기량 → ID'라고 표기할 수는 없다. 동일한 배기량을 갖는 차량이 여러 대 있을 수 있기 때문이다.
함수 종속 역시 정규화와 마찬가지로 6가지가 존재하지만, 주로 3가지만을 고려한다.
-
완전 함수 종속(Full functional dependency)
종속자가 기본키에만 종속되며, 기본키가 여러 속성으로 구성되어 있다면 기본키를 구성하는 모든 속성에 종속된 경우를 말한다.
예를 들어 치킨 주문을 기록한 다음과 같은 테이블이 있다고 하자.고객번호 제품번호 제품명 주문량 001 A1 후라이드 1 002 A2 양념 1 003 A3 순살후라이드 2 004 A4 순살양념 1 이 테이블의 기본키는 '고객번호'와 '제품번호'가 조합된 (고객번호, 제품번호)이다. 이때 주문량을 알기 위해서는 고객번호와 제품번호를 모두 알아야 할 것이다. 따라서 '(고객번호, 제품번호) → 주문량'이며, 주문량은 기본키에 완전 함수 종속되었다고 한다.
-
부분 함수 종속(Partial functional dependency)
테이블에서 종속자가 기본키가 아닌 다른 속성에 종속되거나, 혹은 기본키가 여러 속성으로 구성되어 있을 때 기본키를 구성하는 속성 중 일부에만 종속되는 경우를 말한다.
다시 위의 치킨 주문 테이블을 이용해 보자. 해당 테이블의 기본키는 (고객번호, 제품번호)이다. 그런데 제품명의 경우 고객번호를 몰라도 알 수 있다. 즉 제품명은 기본키를 구성하는 속성 중 일부인 '제품번호'에만 종속되는 것이다. -
아행 함수 종속(Transitive functional dependency)
테이블에서 X, Y, Z라는 3개의 속성이 있을 때, X → Y, Y → Z라는 종속 관계가 있고 X → Z가 성립할 때 이를 이행적 함수 종속이라 한다. 즉, X를 통해 Y를 알 수 있고, 그를 통해 Z를 알 수 있는 경우를 말한다.이번에는 치킨 메뉴 테이블을 가정하여 살펴보자.
제품번호 제품명 가격 A1 후라이드 18000 A2 양념 18500 A3 순살후라이드 19000 A4 순살양념 19500 제품번호(X)를 알면 주문한 제품명(Y)을 알 수 있다. 그리고 제품명(Y)을 알면 가격(Z)을 알 수 있다. 따라서 제품번호(X)를 알면 가격(Z)을 알 수 있게 된다. 즉, '제품번호(X) → 제품명(Y)', '제품명(Y) → 가격(Z)', '제품번호(X) → 가격(Z)'가 성립한다.
이러한 함수 종속성을 판단하여 정규화를 진행하게 된다.
제1정규화(First Normal Form, 1NF)
테이블이 제1정규형을 만족했다는 것은 다음의 세 가지 조건을 만족했다는 의미이다.
- 어떤 테이블에 속한 모든 도메인(domain)이 원자값만으로 되어 있다(즉, 하나의 값을 가진다).
- 모든 속성(attribute)에 반복되는 그룹이 나타나지 않는다.
- 기본키를 사용하여 관련 데이터의 각 집합을 고유하게 식별할 수 있다.
그리고 제1정규형을 만족하지 못하는 테이블에 대하여 제1정규형을 만족하도록 하는 것을 제1정규화라 한다.
다음 테이블의 예를 통해 확인해 보자.
| 고객 ID | 이름 | 전화번호 |
|---|---|---|
| 001 | 이지은 | 111-1111, 111-1112 |
| 002 | 김향기 | 222-2222, 222-2223 |
| 003 | 김유정 | 333-3333 |
1, 2번 인스턴스의 경우 전화번호를 2개씩 가지고 있으며, 따라서 전화번호의 도메인이 원자값이 아니게 된다.
| 고객 ID | 이름 | 전화번호1 | 전화번호2 |
|---|---|---|---|
| 001 | 이지은 | 111-1111 | 111-1112 |
| 002 | 김향기 | 222-2222 | 222-2223 |
| 003 | 김유정 | 333-3333 |
이 경우에는 각 도메인이 원자값이기는 하나, 반복되는 속성(전화번호)이 나타나게 되므로 두 번째 조건을 위반하게 된다.
이 테이블에 대하여 제1정규화를 진행하면 다음과 같이 정리할 수 있다.
| 고객 ID | 이름 | 전화번호 |
|---|---|---|
| 001 | 이지은 | 111-1111 |
| 001 | 이지은 | 111-1112 |
| 002 | 김향기 | 222-2222 |
| 002 | 김향기 | 222-2223 |
| 003 | 김유정 | 333-3333 |
제2정규화(Second Normal Form, 2NF)
제2정규화는 제1정규화를 진행한 릴레이션에 대하여 완전 함수 종속을 만족하도록 테이블을 분해하는 것이다. 다음 테이블의 예를 살펴보자.
| 주문번호 | 음료코드 | 주문수량 | 음료명 |
|---|---|---|---|
| 001 | A01 | 1 | 아메리카노 |
| 002 | A02 | 1 | 카페라떼 |
| 003 | A03 | 2 | 카푸치노 |
기본키가 (주문번호, 음료코드)인 테이블인데, '음료명' 속성의 경우 '음료코드'에만 종속되고 '주문번호'에는 종속되지 않는다. 즉, 부분 함수 종속 상태이다. 따라서 이 경우에는 제2정규화를 통해 주문 테이블과 음료 테이블로 분리한다.
| 주문번호 | 음료코드 | 주문수량 |
|---|---|---|
| 001 | A01 | 1 |
| 002 | A02 | 1 |
| 003 | A03 | 2 |
| 음료코드 | 음료명 |
|---|---|
| A01 | 아메리카노 |
| A02 | 카페라떼 |
| A03 | 카푸치노 |
제3정규화(Third Normal Form, 3NF)
제3정규화는 제2정규화를 진행한 테이블에 대하여 이행 함수 종속이 없도록 테이블을 분해하는 것을 말한다. 즉, 테이블에서 주식별자가 아닌 다른 속성 간에는 서로 함수 종속이 이루어지지 않도록 하는 것이다.
| 주문번호 | 음료명 | 가격 |
|---|---|---|
| 001 | 아메리카노 | 4500 |
| 002 | 카페라떼 | 4800 |
| 003 | 카푸치노 | 4800 |
| 004 | 카페라떼 | 4800 |
상기 테이블의 경우 '가격'이 주식별자인 주문번호가 아니라 '음료명'에 종속되며, 따라서 '주문번호 → 음료명 → 가격'이라는 이행 함수 종속 관계를 나타낸다. 따라서 이를 '주문' 테이블과 '음료' 테이블로 각각 분리하여 정규화를 진행해야 한다.
| 주문번호 | 음료명 |
|---|---|
| 001 | 아메리카노 |
| 002 | 카페라떼 |
| 003 | 카푸치노 |
| 004 | 카페라떼 |
| 음료명 | 가격 |
|---|---|
| 아메리카노 | 4500 |
| 카페라떼 | 4800 |
| 카푸치노 | 4800 |
BCNF 정규화
BNCF 정규화는 제3정규화를 진행한 테이블에 대하여 모든 결정자가 후보키가 되도록 테이블을 분해하는 것이다.
'특강 수강'이라는 가상의 테이블을 예로 들어보자. 이때 하나의 특강은 한 명의 교수가 전담한다고 가정한다.
| 학생번호 | 강의명 | 교수명 |
|---|---|---|
| 001 | AI와 한국어 | 김XX |
| 002 | AI와 한국어 | 김XX |
| 003 | 인터넷과 국어의 역사성 | 최XX |
| 004 | 한국어 빅데이터 처리 | 박XX |
| 005 | 한국어 빅데이터 처리 | 박XX |
위의 테이블에서 기본키는 (학생번호, 강의명)이며, 기본키는 '교수명'을 결정한다. 그런데 교수가 바뀌면 강의명도 바뀌게 되므로 교수명 역시 강의명을 결정하는 결정자이다. 이 경우 결정자인 '교수명'이 후보키가 아니게 되며, 따라서 BCNF 정규화를 통해 테이블을 분할해야 한다. 상기 예의 경우 특강 신청 테이블과 특강 교수 테이블로 분해할 수 있을 것이다.
| 학생번호 | 교수명 |
|---|---|
| 001 | 김XX |
| 002 | 김XX |
| 003 | 최XX |
| 004 | 박XX |
| 005 | 박XX |
| 교수명 | 강의명 |
|---|---|
| 김XX | AI와 한국어 |
| 최XX | 인터넷과 국어의 역사성 |
| 박XX | 한국어 빅데이터 처리 |
반정규화(De-Normalization)
정규화를 통해 이상 현상을 방지하고 데이터베이스의 성능 향상을 도모할 수 있다. 그러나 지나친 정규화로 테이블이 과도하게 분할될 경우 각 테이블 간의 연산(JOIN 연산)이 많아지면서 데이터베이스의 조회 성능이 저하될 수 있다. 따라서 데이터의 일부 중복을 허용함으로써 JOIN 연산을 줄이고 이를 통해 데이터베이스의 조회 성능을 향상시키는 방법이 있는데, 이를 반정규화(De-Normalization)라 한다.
반정규화는 '테이블 반정규화', '컬럼 반정규화', '관계 반정규화' 등의 방법이 있는데, 그중 가장 주요한 것은 '테이블 반정규화'이다.
테이블 반정규화는 다시 '테이블 병합', '테이블 분할', '테이블 추가'로 나눌 수 있다.
테이블 병합
JOIN 연산이 필요한 경우가 많아 테이블을 통합하는 것이 성능 측면에서 유리한 경우 테이블 병합을 고려할 수 있다.
- 1:1 관계 테이블 병합
- 1:M 관계 테이블 병합
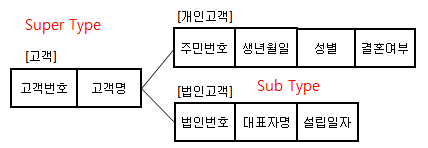
- 슈퍼/서브 타입 테이블 병합
1:M 관계 테이블 병합의 경우 1에 해당하는 테이블의 속성 개수가 많으면 병합했을 경우 중복 데이터가 많아지므로 병합이 적합하지 않으므로 주의한다.
※ 슈퍼/서브 타입
테이블 분할
테이블에서 특정 속성에만 집중적으로 접근하는 경우가 많을 경우 그 속성을 별도의 테이블로 분리하는 것이다.
- 테이블 수직 분할 : 테이블의 일부 속성을 별도의 테이블로 분할(1:1 관계 성립)
- 테이블 수평 분할 : 테이블의 인스턴스를 특정 기준을 잡아 별도의 테이블로 분할(파티셔닝)
※ 예) 주문 이력 데이터를 '연도'별로 구분하여 별도의 테이블로 구분
테이블 추가
- 중복 테이블 추가
- 데이터 중복을 감안하더라도 성능상 필요하다고 판단되는 경우 별도의 테이블을 추가
- 업무가 다르거나 서버가 다른 경우에도 활용 가능
- 통계 테이블 추가 : SUM. AVG 등의 연산을 미리 수행하여 계산치를 저장한 테이블을 추가함으로써 조회 성능을 향상
- 이력 테이블 추가 : 하나의 마스터 테이블에 존재하는 레코드를 중복하여 별도의 이력 테이블에 추가
※ 예) 상품 가격 이력 테이블에서 상품 가격의 변동 이력을 관리 - 부분 테이블 추가 : 하나의 테이블에서 자주 이용하는 특정 속성들이 있을 때 해당 속성들을 별도로 모아 두는 테이블
기타 반정규화 방법
-
컬럼 반정규화
- 중복 컬럼 추가 : 프로세스상 JOIN이 필요한 경우가 많아 컬럼(속성)을 추가하는 것이 성능 측면에서 유리할 경우 고려하는 방법
- 파생 컬럼 추가 : 프로세스 수행 시 부하가 우려되는 계산값을 미리 컬럼으로 추가하여 보관하는 방식
※ 예) 상품 재고, 프로모션 적용 할인가 등 - 이력 테이블 컬럼 추가 : 대량의 이력 테이블을 조회할 경우 성능이 저하될 것을 대비하여 조회 기준이 될 것으로 판단되는 컬럼을 미리 추가해 두는 방식
※ 예) 최신 데이터 여부 등
-
관계 반정규화
업무 프로세스상 JOIN이 필요한 경우가 많아 중복 관계를 추가하는 것이 유리할 경우 고려하는 방법이다.
반정규화를 통해 데이터의 조회 성능을 높일 수 있다. 그러나 반대로 데이터의 삽입, 삭제, 수정 등의 수행 시에는 연산이 많이 필요하게 되어 성능이 저하될 수 있으므로 적절한 수준에서 반정규화를 실시해야 한다. 또한 데이터의 일관성이 깨질 수도 있으므로 반정규화 시 데이터 일관성 유지를 위한 방안을 함께 고려해야 한다.