Database I/O
디스크(Disk) 접근 시간
물리 디스크에서 데이터에 접근하기 위해서는 디스크 헤드(Head, 디스크 암의 끝에서 디스크와 맞닿는 부분)를 움직여 데이터가 저장된 트랙(Track, 디스크의 한 면에서 중심으로부터 같은 거리에 있는 섹터들의 집합)에 위치시고 실제 데이터가 저장된 섹터(Sector, 데이터가 저장되는 물리적 단위)가 올 때까지 기다려야 한다. 이때 소요되는 시간을 디스크 접근 시간이라고 하는데, 디스크 접근 시간은 '탐색 시간 + 회전 지연 시간 + 전송 시간'으로 정의할 수 있다.
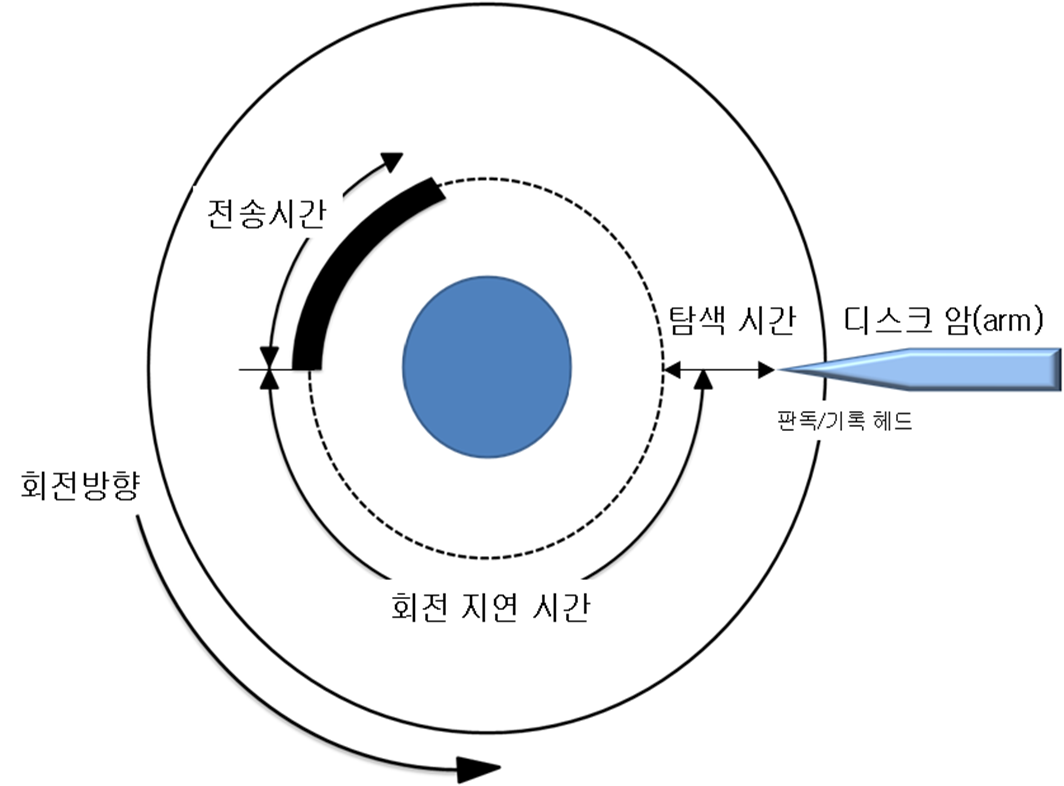
- 탐색 시간(Seek time)
디스크 헤드가 원하는 트랙에 위치하는 데까지 걸리는 시간으로, 회전 지연 시간과 전송 시간에 비해 압도적으로 오래 걸린다(둘을 합쳐도 탐색 시간보다 짧다). - 회전 지연 시간(Rotational delay time)
디스크(플래터)가 회전하면서 탐색하고자 하는 데이터가 헤드까지 오는 데 걸리는 시간이다. - 전송 시간(Transmission time)
헤드가 읽은데이터를 메인 메모리로 전송하는 데 걸리는 시간이다.
Sequential I/O vs Random I/O
인덱스에 대해 이해하기에 앞서 디스크에 접근하는 두 가지 방식에 대해 간단히 짚고 넘어가자.
- Sequential I/O
- 물리적으로 인접한 페이지를 차례대로 읽는 접근 방식
Full table scan시 사용됨
- Random I/O
- 물리적으로 불연속적인 페이지를 임의로 읽는 방식
Index range scan시 사용됨
이 두 방식을 분리한 이유는 무엇일까? 여러 개의 데이터를 입력할 때 순차 I/O(Sequential I/O)는 디스크 헤드를 한 번만 움직이지만 랜덤 I/O(Random I/O)는 디스크 헤드를 여러 번 움직여야 한다.
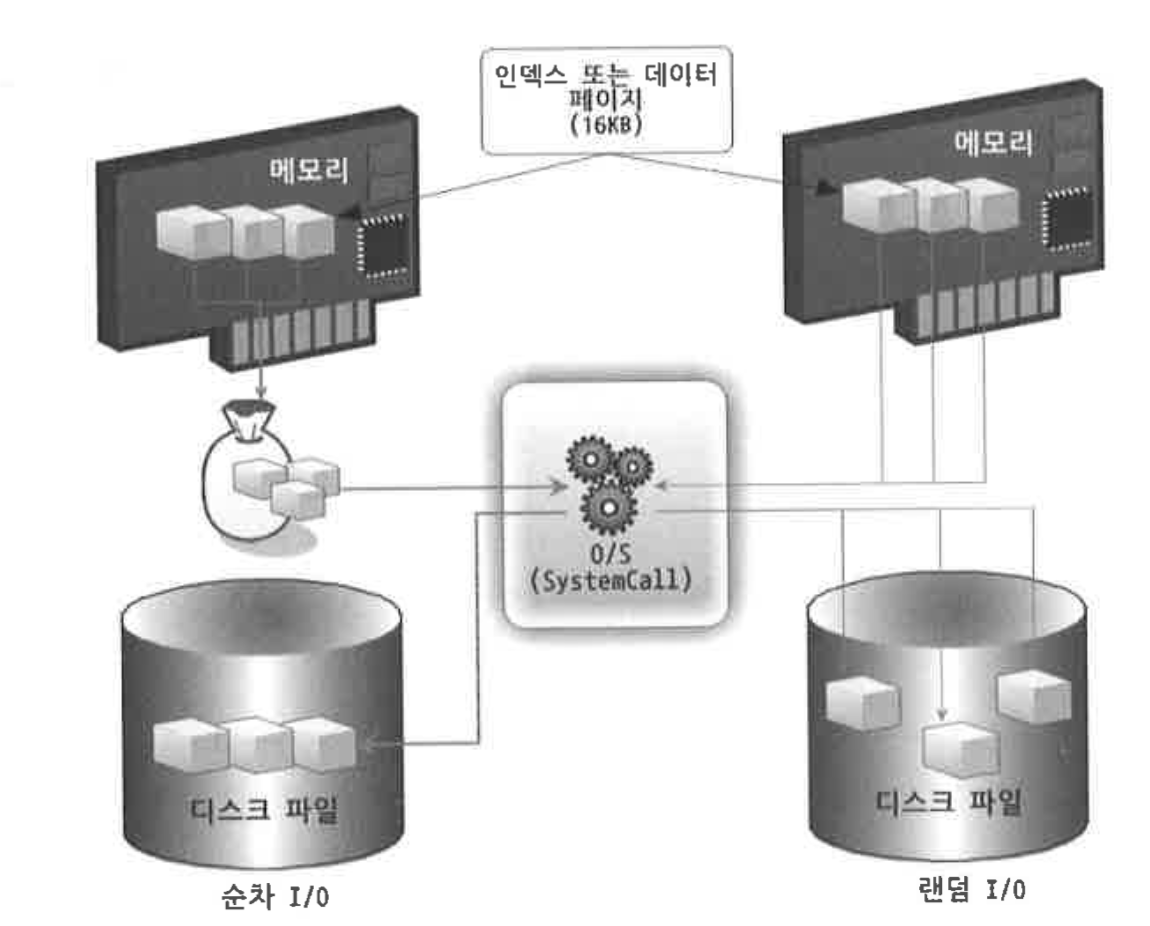순차 I/O는 3개의 페이지에 대해 시스템 콜(디스크 헤드 이동)을1번 요청한 반면, 랜덤 I/O는 3번 요청한다.
그런데 앞서 디스크 접근 시간에 대해 설명하면서 디스크 헤드를 움직이는 시간(탐색 시간)이 디스크 접근 시간 중 가장 큰 비중을 차지한다고 하였다. 즉, 디스크에 데이터를 읽고 쓰는 데 걸리는 시간은 디스크 헤드의 이동을 얼마나 줄이느냐에 의해 결정된다고 볼 수 있다.
HDD와 달리 SSD에는 디스크 원판이 없으므로 순차 I/O와 랜덤 I/O의속도 차가 없을 것으로 생각할 수 있지만, SSD에서도 랜덤 I/O는 순차 I/O 대비 처리율(Throughput)이 떨어진다. 이는 랜덤 I/O 시 SSD에서 사용하는 '매핑 테이블'의 업데이트가 발생하기 때문이다.
RDBMS는 디스크에 대하여 I/O 작업이 빈번히 발생하므로 MySQL 서버에서는 그룹 커밋이나 바이너리 로그, InnoDB 로그 버퍼 등의 기능을 내장하여 랜덤 I/O의 부하를 줄여 주고 있다.
InnoDB 버퍼 풀
디스크의 데이터 파일 혹은 인덱스 정보를 메인 메모리 내에 캐시해 두는 영역을 말한다. 버퍼 풀을 통해 자주 접근하는 데이터를 메모리에서 바로 획득할 수 있으며, 쓰기 작업을 지연시켜 일괄처리가 가능하도록 하는 버퍼 역할도 한다. 이를 통해 전체 작업의 수행 속도를 증가시킬 수 있다.
MySQL을 위한 서버에서는 물리 메모리의 최대 80%까지를 InnoDB의 버퍼 풀로 할당하여 사용하는 경우가 많다.
쿼리를 튜닝한다고 하여 때 랜덤 I/O를 순차 I/O로 변경하는 경우는 많지 않다. 따라서 쿼리 튜닝의 목적은 랜덤 I/O 자체를 줄이는 것이다. 이때 랜덤 I/O를 줄인다는것은 랜덤 I/O를 수행하되 꼭 필요한 데이터만 읽도록 쿼리를 개선하는 것을 의미한다.
Index
개요
인덱스(Index)란 추가적인 쓰기 작업을 수행하고 저장 공간을 할당하여 데이터베이스 테이블의 검색 속도를 향상시키기 위한 자료 구조이다. 흔히 책의 말미에 있는 '찾아보기'로 비유하곤 하는데(사실 찾아보기의 영번역이 index이다), 책에서 원하는 단어(즉, 데이터)가 어디에 위치했는지 쉽게 파악할 수 있도록 해당 단어의 위치를 표시한 것처럼, 데이터베이스에서도 데이터와 데이터의 위치를 포함한 자료 구조를 생성하여 빠르게 조회할 수 있도록 하는 것이다.
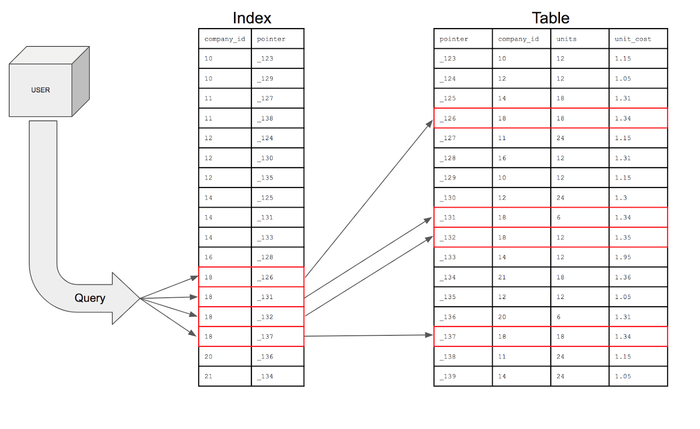
DBMS의 인덱스는 Sorted list의 형태를 띠고 있는데, 이는 인덱스 자체의양도 많아질 경우 인덱스를 빠르게 찾을 수 있도록 하기 위함이다. 다만 이러한 구조로 인해 매번 새로운 값을 넣거나 값을 수정할 때마다 값이 정렬되어야 하며, 따라서 인덱스가 많을 경우 CUD(Create, Update, Delete) 작업의 처리 속도는 느려지게 된다.
즉, Index는 CUD에 대한 성능을 일부 희생하고, 대신 데이터의 읽기 속도를 높이는 기능이다.
인덱스의 역할별 구분
- 기본키(Primary Key, PK)
레코드(인스턴스)를 대표하는 컬럼의 값으로 만들어진 인덱스로, Null값을 허용하지 않으며 중복 역시 허용하지 않는다. - 보조키(Secondary Key)
기본키를 제외한 모든 나머지 인덱스를 말한다.
인덱스의 중복 허용 여부 구분
- 고유 인덱스(Unique index)
컬럼의 값이 유일한 경우, 즉 중복이 존재하지 않을 경우 만들 수 있는 인덱스 - 비고유 인덱스(Non-Unique index)
컬럼 값에 중복된 값이 있는 경우 만들 수 있는 인덱스
여기까지가 인덱스를 구분하는 간단한 기준이고, 인덱스를 저장 방식(알고리즘)별로 구분하면 대표적으로 B-Tree index, Hash index 등이 있다.
B-Tree index
Tree algorithm
B-Tree를 이해하기에 앞서 우선 트리 구조가 무엇인지 확인해 보자.
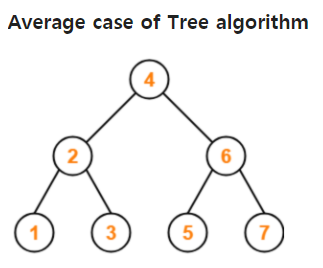
일반적으로 Tree 구조는 탐색에 대한 시간 복잡도로 O(logN)을 가지지만, 트리가 어떻게 구성되느냐에 따라 달라질 수 있다. 예컨대 다음과 같은 최악의 경우 시간 복잡도가 O(N)이 된다.
.png)
이러한 문제를 방지하기 위해 사용하는 것이 밸런스 트리(Balanced tree)이다. 밸런스 트리는 트리의 노드가 한 방향으로 쏠리지 않도록 노드 삽입 혹은 삭제 시 어떤 규칙에 따라 노드를 재정렬하여 트리의 양쪽 노드의 밸런스를 유지하는 트리이다.
B-Tree
B-Tree는 이진 트리(하나의 노드가 가질 수 있는 자식 노드가 최대 2개인 트리)를 확장한 트리로서 하나의 노드가 여러 개(2개 이상)의 자식 노드를 가질 수 있으며, 동시에 밸런스 트리이므로 모든 리프 노드가 같은 깊이(Depth)를 갖도록 설계된 트리이다.
B-Tree의 최상단에 위치하는 단하나의 노드를 루트 노드(Root nodde)라고 하고 최하위의 노드들을 리프 노드(Leaf node)라고 한다. 그리고 그 중간에 존재하는 노드들을 가지 노드, 즉 브랜치 노드(Branch node)라고 한다.
B-Tree는 노드 하나에 여러 개의 키와 각 키에 대응하는 데이터를 저장할 수 있으며, 데이터와 데이터 사이의 범위를 이용하여 자식노드를 갖는다(따라서 자식 노드의 개수는 n+1개이다).
이때 같은 노드에 저장된 데이터는 배열로 저장되어 있으며, 실제 메모리상에서도 순차적으로 저장되어 있다. 따라서 동일한 노드의 데이터들에 대해 접근할 때는 포인터 접근이 아니라 실제 메모리상에서 바로 다음 인덱스로 접근하게 된다.
B-Tree는 이러한 특징으로 인해 다음과 같은 장점을 가진다.
- 항상 정렬된 상태이므로 부등호 연산이 가능하다.
- 참조 포인터가 적어 데이터의 양이 많아도 빠른 메모리 접근이 가능하다.
- 데이터 탐색뿐만 아니라 저장, 수정, 삭제 시에도 항상 O(logN)의 시간복잡도를 가진다.
- 어떤 값에 대해서도 동일한 시간에 결과를 얻을 수 있다(이를
균일성이라고 한다).
B+Tree
B+Tree는 B-Tree로부터 변형된 트리 구조로, 모든 노드에 인덱스와 데이터(value)를 함께 저장했던 B-Tree와 달리 Leaf node에만 인덱스와 데이터를 저장하고, 나머지 노드들은 자식 노드의 인덱스만을 갖는다. 그리고 Leaf node들은 Linked list로 연결되어 있다.
B+Tree는 다음과 같은 장점을 가진다.
- 리프 노드를 제외하면 데이터가 저장되지 않으므로 메모리를 더 확보할 수 있으며, 이를 통해 더 많은 인덱스를 수용할 수 있다.
- 하나의 노드에 더 많은 인덱스를 담을 수 있으므로 트리의 높이가 낮아지며, 따라서 cache hit를 높일 수 있다.
- 풀 스캔 시 데이터가 리프 노드에만 있으므로 한 번의 선형탐색만으로도 스캔이 가능하다(B-Tree의 경우 모든 노드를 확인해야 한다).
Change buffer
체인지 버퍼(Change buffer)는 보조 인덱스 페이지가 버퍼 풀에 없을 경우 변경 사항을 캐시하는 데이터 구조이다. 보조 인덱스의 경우 유니크하지 않고 정렬되지 않은 채 처리되므로 최신 상태로 유지하는 데는 상당한 I/O가 발생하며, 이를 보완하기 위해 DML 작업 시 변경 사항을 실시간으로 업데이트하지 않고 체인지 버퍼를 통해 변경 사항을 캐시하는 것이다.
- 보조 인덱스에 대한 INSERT, UPDATE, DELETE 요청 시 Buffer pool에 키값을 추가할 페이지(B+Tree의 leaf node) 존재 여부를 확인
- 페이지가 존재할 경우 즉시 키 변경(삽입, 수정, 삭제) 작업을 처리
- 페이지가 없을 경우 Buffer 영역에 인덱스 레코드 조각(변경할 키 값과 레코드 주소)을 임시로 저장하고 작업 완료 처리
- 인덱스 페이지를 읽을 때마다 Buffer 영역에 병합(Merge)해야 할 키 값이 있는지 확인하고, 있을 경우 병합 실행(B+Tree에 키와 주소를 저장)
- 서버 자원에 여유가 생길 경우 버퍼에 임시로 저장된 인덱스 레코드 조각을 백그라운드 스레드(체인지 버퍼 머지 스레드)를 이용해 병합
InnoDB의 Record lock
스토리지 엔진인 InnoDB에서는 레코드 락, 갭 락, 넥스트 키 락, 오토 인크리먼트 락 등의 락을 제공한다. 그중 레코드 락은 인덱스 레코드에 락을 걸어 다른 트랜잭션의 접근을 막는 것이다. 이때 실제 테이블의 레코드에 대해 락을 거는 것이 아니라 인덱스 레코드에 락을 걸게 되고, 별도로 생성한 인덱스가 없는 테이블은 InnoDB가 자체적으로 생성한 클러스터 인덱스를 이용해 락을 건다.
아래 예를 통해 이해해보자.
SELECT COUNT(*) FROM employees WHERE first_name="김" -- 300건 조회된다고 가정 SELECT COUNT(*) FROM employees WHERE first_name="김" AND last_name="철수" -- 1건 조회된다고 가정 UPDATE employees SET hire_date=NOW() WHERE first_name="김" AND last_name="철수" -- 어디에 락이 걸릴 것인가?만약 first_name 컬럼에만 인덱스(보조 인덱스)가 적용되어 있다고 하면, 마지막 UPDATE 쿼리에서 락이 걸리는 레코드는 몇 개일까? 실제 업데이트되는 것은 성이 '김'이고 이름이 '철수'인 레코드 한 건이지만 InnoDB는 인덱스가 있는 first_name에 락을 걸게 되므로 300건의 레코드에 락이 걸리게 된다. 만약 위의 경우에서 first_name이 동일한 레코드가 많이 있다면 불필요하게 많은 레코드에 락이 걸림으로써 DB의 성능이 저하될 것이다.
즉, 인덱스의 설정에 따라 레코드의 잠금 범위가 달라질 수 있으므로 인덱스를 신중하게 설정해야 한다.
※ 사실 체인지 버퍼와 레코드 락은 인덱스 자료구조에 대한 직접적인 내용은 아니고 모두 InnoDB에 대한 내용에 해당하는데, B+Tree가 InnoDB와도 연관이 있어 여기서 간단히 정리해 두었다.
인덱스 사용에 영향을 주는 요소
B+Tree 인덱스는 인덱스를 구성하는 키 값의 크기, 컬럼 순서, 카디널리티 등 다양한 요소로 인해 검색이나 변경 작업 등의 성능이 영향을 받는다.
인덱스 키 값의 크기
InnoDB의 페이지 크기는 16KB로 고정되어 있다. 따라서 인덱스 키가 16바이트라면 하나의 페이지에 대략 585개의 키를 저장할 수 있다. 그런데 키의 크기가 32바이트로 늘어난다면 하나의 페이지에 약 372개의 키를 저장할 수 있게 된다.
만약 클라이언트가 SELECT 쿼리로 500개의 레코드를 읽으려고 할 때, 전자의 경우 한번의 I/O로 해결할 수 있지만 후자의 경우 2회의 I/O가 필요하다. 즉, 인덱스를 구성하는 키 값의 크기가 커지면 DB의 성능도 저하될 수 있다.
인덱스의 컬럼 순서
인덱스는 PK를 포함하여 여러 개의 컬럼으로 구성될 수 있으며, 이를 다중 컬럼 인덱스(Multi-column index)라고 부른다. 이 다중 컬럼 인덱스에서 중요한 것은 현재의 컬럼은항상 이전 컬럼에 의존하여 정렬된다는 것이다. 예를 들어 employee 테이블에 dept_no와 emp_no 컬럼을 인덱스로 설정하면 emp_no만으로 질의하는 경우 인덱스를 제대로 타지 못하게 된다(emp_no는 첫 번째 인덱스 컬럼인 dept_no가 동일한 레코드에서만 의미가 있으므로). 따라서 인덱스 컬럼의 순서는 DB의 성능에 매우 중요한 영향을 미친다.
카디널리티(Cardinality)
카디널리티란 특정 컬럼에 존재하는 데이터의 고유성을 의미한다. 즉, 카디널리티가 높다는 것은 중복 데이터가 적고 유니크한 값이 많다는 의미이다. 그리고 일반적으로는 값이 유니크한 경우 검색 대상이 줄어들어 질의의 처리가 빠르다.
인덱스 읽기 방식의 분류
인덱스 레인지 스캔(Index range scan)
인덱스 레인지 스캔은 범위가 결정된 인덱스를 읽는 방식으로서, 정해진 범위에만 접근하면 되기 때문에 다른 방식보다 속도가 빠르다. 일반적으로 '인덱스를 탄다'고 하면 인덱스 레인지 스캔으로 데이터를 조회하는 것을 의미한다.
우선 루트 노드로부터 비교를 시작해 리프 노드에 도달하고, 리프 노드에서 시작 위치를 찾으면 그 지점부터 순차적으로 스캔을 시작한다. 그리고 범위 마지막에 해당하는 데이터까지 스캔하면 데이터를 사용자에게 반환하고 쿼리를 종료한다.
이때, 데이터 파일에서 레코드를 읽어올 때 레코드 한 건마다 랜덤 I/O가 발생한다(따라서 인덱스를 이용해 데이터를 읽는 작업은 비용이 많이 발생한다).
인덱스 풀 스캔(Index full scan)
인덱스 풀 스캔은 말 그대로 인덱스의 처음부터 끝까지 모두 스캔하는 방식이다. 이 방법은 쿼리나 인덱스가 PK만을 필요로 할 때 사용되고, 그 외의컬럼이 필요한 경우 절대 사용되지 않는다. 또한쿼리의 조건절에 사용된 컬럼이 인덱스의 첫 번째 컬럼이 아닌 경우(예를 들어 인덱스가 A, B, C 순으로 되어 있으나 조건절은 B 또는 C 컬럼으로 검색되는 경우)에도 이 방식이 사용된다.
인덱스 레인지 스캔에 비해서는 느린 방식이지만 테이블 풀 스캔보다는 적은 I/O로 쿼리를 처리할 수 있다. 다만 인덱스 풀 스캔은 일반적으로 '인덱스를 사용한다'고 하지 않는다.
루즈 인덱스 스캔(Loose index scan)
루즈 인덱스 스캔은 인덱스를 느슨하게, 듬성듬성 스캔하는 방식이다. 일반적으로 GROUP BY나 MIN. MAX 등의 집합 함수를 사용하는 쿼리를 최적화할 때 사용되며, 불필요한 인덱스는 무시하고 넘어가는 형태로 처리된다.
인덱스 스킵 스캔(Index skip scan)
인덱스 스킵 스캔은 MySQL 8.0버전에 추가된 최적화 기능으로, 조건절에 첫 번째 인덱스가 없을 경우에도 두 번째 인덱스만으로 인덱스를 검색할 수 있도록 옵티마이저가 자동으로 쿼리를 최적화하여 인덱스를 타도록 하는 읽기 방식이다.
인덱스 스킵 스캔이 실행되기 위해서는 다음의 조건을 모두 만족해야 한다.
- 조회되는 컬럼은 인덱스만으로 처리할 수 있어야 한다(커버링 인덱스).
- 인덱스의 선행 컬럼은 WHERE 절에 없어야 한다.
- 인덱스 선행 컬럼의 카디널리티가 낮아야(유니크한 값이 적어야) 한다.
Hash index
해시 인덱스는 일반적인 DBMS에서 메모리 기반의 테이블을 구현하는 데 주로 사용된다. B+Tree와 달리 버켓으로 구성되는데, 여기서 버켓은 인덱스 엔트리가 저장되는 공간을 말한다. 검색하고자 하는 값을 입력하면 해시 함수를 거쳐 나온 값을 이용해 찾고자 하는 키 값이 포함된 버켓을 찾아내는 것이다.
해시 함수는 실제 저장 위치를 빠르게 알 수 있으며, 해시 함수로 변환된 값을 저장하므로 컬럼의 길이가 길어도 저장되는 양은 현저히 줄어든다는장점이 있다.
그러나 함수의 결괏값의 범위가 넓어질수록 버켓도 많이 필요하게 되어 공간의 낭비가 심해지고, 해시함수를 거쳐 변형된 값을 사용하므로 범위를 검색하거나 원본값을 기준으로 정렬하는 등의 행위가 불가능하다.
즉, 해시 인덱스는 범위 검색(>=, BETWEEN AND, ><, LIKE) 혹은 원본값을 기준으로 하는 정렬(ORDER BY, DESC 등)은 불가능한 대신 동등비교조건(==, IN, IS NULL. IN NOT NULL 등)인 경우 B+Tree보다 훨씬 바르게 질의를 처리할 수 있다.
참고 자료
