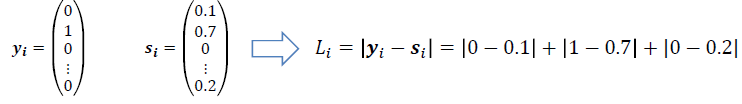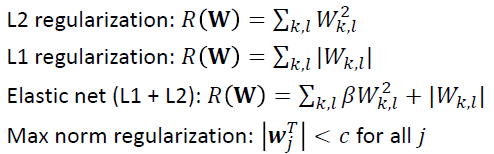Loss Function and Optimization

How can we tell whether weight of a linear classifier W is good or bad?
To quantify a "good" W, loss function is needed.
Starting with random W and find a W that minimizes the loss to optimize weights of a linear classifier.

Type of loss function

(1) Hinge Loss

✔ Binary hinge loss (=binary SVM loss)

There are only two classes: positive or negative.
(1) If $i^{st}$ image is in positive class, then class label $y_i$ is $+1$,
(2) If $i^{st}$ image is in negative class, then class label $y_i$ is $-1$.

To minimize the loss ($\to$ $L_i=0$), $y_i\times s\geq1$ should be satisfied.
There are two cases where $y_i\times s\geq1$:
(1) $i^{st}$ sample is in positive class: $y_i = 1,\quad then\; s \geq 1$
(2) $i^{st}$ sample is in negative class: $y_i = -1,\quad then\; s \leq -1$
∴ There are margin (1 ~ -1) between positive class and negative class.

✔ Hinge loss (=multiclass SVM loss)

For the number of class $c(>2)$,

To minimize the loss (=$L_i=0$), $s_{y_i}-s_j\geq1$ should be satisfied.
In other word, $i^{st}$ image is in $y_{i}^{st}$ class should be satisfied the following condition:

$\begin{aligned} s_{y_i}-s_1&\geq1\\ s_{y_i}-s_2&\geq1\\ ...\\ s_{y_i}-s_{y_i-1}&\geq1\\ s_{y_i}-s_{y_i+1}&\geq1\\ ...\\ s_{y_i}-s_{c}&\geq1 \end{aligned}$

∴ There are margin 1 between $y_i$ class and other classes.
∴ $y_{i}^{st}$ class must have the largest $s$ value, and must be at least 1 greater than the $s$ value of the other classes.

(2) Log Likelihood Loss

Where $j$ satisfies $z_{ij}=1$,

P is not a score, but probability.
$p_j$ is a probability that the $i^{th}$ image belongs to the $j^{th}$ class.
⁕ class label for $i^{th}$ image $z_{ij}$ is $0$ or $1$

As $p$ is closer to $1$, loss is minimized. ( ∵$-\log(1) = 0)$

Let's suppose that $i^{th}$ image belongs to class 2$(j=2)$ and $c$=10 .
Then $z_i, L_i$ are as below :

(3) Cross-entropy Loss

(1) If $z_{ij}=0$, then sum $-\log (1-p_j)$ to $L_i$.
(2) If $z_{ij}=1$, then sum $-\log (p_j)$ to $L_i$.

⁕ Softmax Activation Function

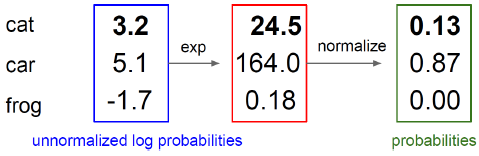
Probability is proportional to $e^{score}$, so we can compute probability using scores. The function below is the softmax activation function.

✔ Softmax + Log likelihood loss:

We can apply Log likelihood loss using probabilites of softmax function.
This is often called 'softmax classifier'.

✔ Softmax + Cross-entropy loss:

We can apply Cross-entropy loss using probabilites of softmax function.

✔ Compare with SVM (Hinge loss)

Softmax Classifier constantly tries to make the loss small because the loss never becomes zero.
However, if the margin is 1 or higher, the SVM does not try to reduce the loss because the loss is already zero.

(4) Regression Loss

Regression Loss function is widely used in pixel-level prediction. (Ex) image denoising
Using L1 or L2 norms :

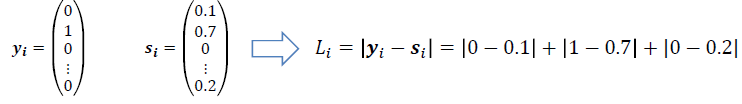
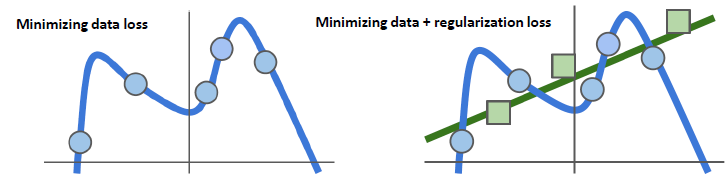
Regularization

Suppose that we found a W such that L=0.
Is this W unique?
No. $2\times W$ is also has L=0.

For this reason, regularization loss is needed.
In the function below, $λR(W)$ is the part of regularization.

✔ 4 types of Regularization:

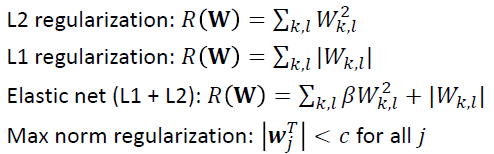
Optimization

(1) Gradient Descent

Gradient Descent is the most simple approach to minimizing a loss function.

(2) Stochastic Gradient Descent(SGD)

Full sum is too expensive when N is large.
Instead, approximate sum using a minibatch of examples 32/64/128 common.