수업 40일차

✔ 추론 통계

검정

유의 수준과 기각역

• 유의 수준 (Significance Level)
  - 귀무 가설 기각과 채택을 위해서 설정하는 기준값
  - 보통은 1%, 5%를 채택합니다.
• 유의 확률(p-value)이 유의 수준으로 정한 값보다 작다는 것은, 해당 검정 통계에서 이 검정 통계치가 나올 수 있는 확률이 아주 작다는 의미이므로 가장 근본이 되는 가설, 즉 귀무 가설이 틀렸다는 의미로 해석해서 귀무 가설을 기각함
• 유의 확률이 유의 수준보다 크다면, 해당 검정 통계에서 이 검정 통계치가 나오는 것이 불가능하지만은 않다는 의미이므로 귀무 가설을 기각할 수 없음
• 유의 수준에 대해 계산된 검정 통계량을 기각역(Critical Value) 하는데, 기각역을 알고 있다면 유의 확률을 유의 수준과 비교하지 않고 검정 통계량을 직접 기각역과 비교해서 기각 여부를 판단할 수 있음

신뢰구간

• 모수가 어느 범위 안에 있는지를 확률적으로 보여주는 방법
• 표본의 개수가 많을수록 신뢰 구간은 작아지고, 신뢰 수준이 클수록 신뢰 구간도 커짐
• 신뢰 구간과 가설 검정을 통해서 모수의 총량(평균이나 표준편차)에 대해서 알 수 있으며, 데이터 각각에 대해서는 모르며, 데이터 각각에 대해서 알고자 하는 경우, 머신러닝을 사용합니다.

• 어떤 제조회사의 부품에 대한 95% 신뢰구간이 [100mm ~ 120mm]라고 한다면, 부품이 100mm ~ 120mm 사이일 가능성이 95%라고 확신할 수 있다.
• 표본을 100개 추출했을 때, 95개 정도가 [100mm ~ 120mm] 사이에 존재한다.

자유도

• 표본 데이터에서 계산된 통계량에 적용되는데, 변화가 가능한 값들의 개수
• 데이터의 개수 - 1
• 표본을 통해서 모집단의 분산을 추정하고자 하는 경우, 분모에 n(데이터의 개수)을 대입하면 추정치가 약간 아래로 편향될 것이기에 분모에 데이터의 개수 -1을 사용하면 추정값에 편향되지 않습니다.
• 회귀 분석에서 완전히 불필요한 예측 변수들이 있으면 회귀 알고리즘을 사용하기 어려워지기 때문에 -1을 하는 것을 권장합니다.

• 월요일부터 일요일이 존재한다고 가정할 때, 월요일부터 토요일까지를 결정하면, 토요일 다음은 무조건 일요일이 됩니다.
• 일요일은 토요일에 종속되게 됩니다.
• 회귀 분석을 할 때, 하나의 값에 의해서 다른 하나의 값이 결정된다면 다중 공선성 문제가 발생
• 회귀분석을 할 때, feature들 사이의 관계를 잘 파악해야 합니다.
• feature의 중요도 같은 것을 판단할 때 중요합니다.
• 데이터 과학에서는 자유도를 중요하게 생각하지 않지만, 머신러닝에서능 중요하게 평가합니다.

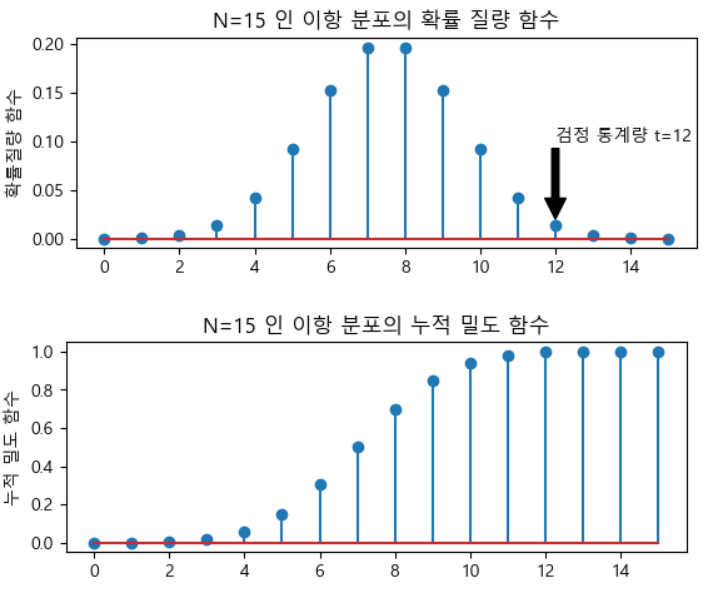
• 어떤 동전을 15번 던졌을 때, 앞면이 12번 나온 경우에, 이 동전은 공정한 것인가?
  - 유의 수준을 5%라 하자
  - 귀무 가설 : 15번 던졌을 때, 12번 정도 나오는 것은 공정하다
  - 동전은 앞 뒷면만 존재하기에 이항(베르누이) 분포이다.

# 시행 횟수
N=15
# 앞면이 나올 확률
mu=0.5
# 이항 분포를 생성
rv=sp.stats.binom(N,mu)
xx=np.arange(N+1)
# 확률 질량 함수를 출력 (pmf)
# 각각이 나올 수 있는 확률에 대한 함수가 확률 질량 함수이다.
plt.subplot(211)
plt.stem(xx,rv.pmf(xx))
plt.ylabel('확률질량 함수')
plt.title('N=15 인 이항 분포의 확률 질량 함수')
plt.annotate('검정 통계량 t=12', xy=(12,0.02),xytext=(12,0.1),
             arrowprops={'facecolor':'black'})
plt.show()
# 12이 나올 확률
# print(rv.pmf(12-1))
# 이거 말고 누적 밀도함수(cdf)로 봐야한다.
plt.subplot(212)
plt.stem(xx,rv.cdf(xx))
plt.ylabel('누적 밀도 함수')
plt.title('N=15 인 이항 분포의 누적 밀도 함수')
plt.show()
# 유의 확률
x=2*(1-rv.cdf(12-1))
print(x) #0.035

• 유의 수준을 5%로 설정한 경우, 유의 확률이 유의 수준보다 낮기 때문에, 귀무 가설을 기각합니다.
  - 이 동정은 공정하지 않다.

A/B 검정

• 2가지 방법이나 절차 중, 어느 한쪽이 다른 쪽보다 더 우월하다는 것을 입증하기 위해서 실험군을 두 그룹으로 나누어 진행하는 실험
  - 아무런 조치도 취하지 않은 그룹은 대조군, 어떤 조치를 취한 그룹은 처리군이라고 해서, 조치를 취했을 때, 처리군이 대조군보다 더 낫다는 것을 가설로 설정
• 활용 분야
  - UI 개선 , 가격 개선(이벤트)
  

t 검정

• 검정 통계량으로 스튜던트 t 분포를 가진 통계량을 사용
• 표본 평균의 분포를 근사화하기 위해 개발
• 단일 표본 t 검정
  - 정규 분포의 표본에 대해 기대값을 조사하는 검정 방법
  - scipy의 stats 서브 패키지의 ttest_1samp 함수를 사용
  - 표본 데이터 배열과 귀무 가설의 기대값을 대입해서 사용
  

• 성적 데이터가 있을 때, 평균이 몇 점이라고 할 수 있는가?
• tdata.csv 파일의 성적을 읽어서, 평균이 75점이라고 할 수 있는지 유의 수준 5%로 검정해보자.

# tdata.csv 파일의 성적을 읽어서 평균이 75점이라고 할 수 있는지 
# 유의 수준 5% 로 검정하자
items=pd.read_csv('./data/tdata.csv', encoding='cp949')
# items.head()
# 성적의 평균이 75라고 했을 떄의 유의 확률
result=sp.stats.ttest_1samp(items['성적'], popmean=75).pvalue
# print(result)
if result>=0.05:
    print("유의 확률이 유의 수준보다 크므로 귀무 가설 채택")
    print("평균은 75라고 할 수 있습니다.")
else:
    print("유의 확률이 유의 수준보다 작으므로 귀무 가설 기각")
    print("평균은 75라고 할 수 없습니다.")

독립 표본 t 검정

• 서로 독립적인 2개의 샘플의 모수가 같은지 비교
• ttest_ind함수를 이용
• 독립적인 샘플이므로 분산이 같은지 여부를 설정
• 서로 독립적인 2개의 샘플의 모수를 비교할 때는 데이터가 많아야 합니다.
• 데이터의 개수가 적으면 2종 오류(귀무 가설이 거짓인데 진실로 나오는 경우) 발생 가능성이 높아짐

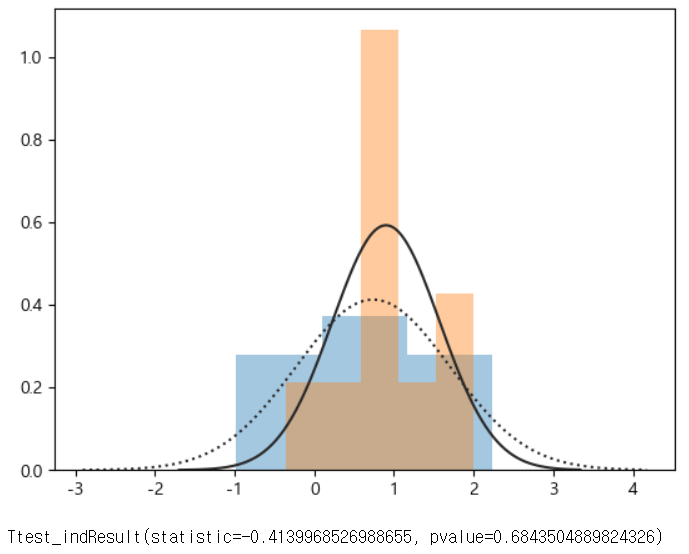
# 첫 번쨰 데이터 집단
N_1=10
mu_1=0
sigma_1=1
# 두 번쨰 데이터 집단
N_2=10
mu_2=0.5
sigma_2=1
# 데이터 생성
np.random.seed(0)
x1=sp.stats.norm(mu_1,sigma_1).rvs(N_1)
x2=sp.stats.norm(mu_2,sigma_2).rvs(N_2)
# print(x1)
# print(x2)
ax=sns.distplot(x1,kde=False,fit=sp.stats.norm, label='1번 데이터 집단')
ax=sns.distplot(x2,kde=False,fit=sp.stats.norm, label='2번 데이터 집단')
ax.lines[0].set_linestyle(":")
plt.show()
print(sp.stats.ttest_ind(x1,x2,equal_var=False))
# 유의 확률이 0.684
# 유의 수준을 얼마로 지정하더라고 귀무 가설을 기각할 수 없음
# 분명히 평균이 0과 0.5 다른데도 두 집단의 평균이 같다는 유의확률이 0.684
# 귀무 가설이 거짓인데 참이라고 나왔습니다.
# 이런 경우를 2종 오류라고 하며, 원인은 대부분 데이터 개수의 부족

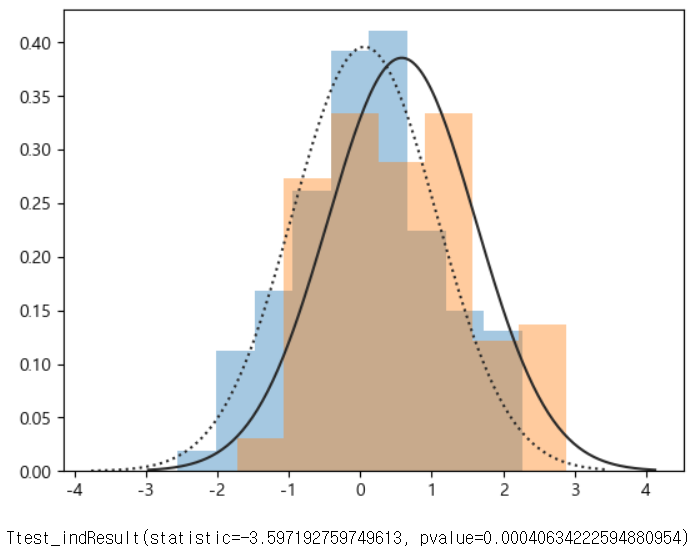
• 두 집단의 데이터 개수를 이전보다 크게(10->100) 설정해서 해결할 수 있다.
  

• 서로 다른 10명에게 수면제 1을 복용했을 때 수면 증가 시간과, 수면제 2를 복용했을 때 수면 증가 시간을 조사한 경우, 수면제 1과 2의 성능이 같다고 할 수 있을까?

# 서로 다른 수면제를 복용한 경우,
# 약의 효과가 다른지 여부를 판단해보자.
# pvalue가 0.05보다 크다면 귀무가설 채택
# 채택한다면 두개의 평균은 같다.
x1=np.array([0.7, -1.6, -0.2, -1.2, -0.1, 3.4, 3.7, 0.8, 0.0, 2.0])
x2=np.array([1.9,0.8, 1.1, 0.1, -0.1, 4.5, 5.5, 1.6, 4.6, 3.4])
r=sp.stats.ttest_ind(x1,x2, equal_var=True)
# print(r)
if r.pvalue>=0.05:
    print("유의 확률이 유의 수준보다 크므로 귀무 가설 채택")
    print("두 수면제의 평균은 같다.")
else:
    print("유의 확률이 유의 수준보다 작으므로 귀무 가설 기각")
    print("두 수면제의 평균은 다르다.")

대응 표본 t 검정

• 두 집단의 샘플이 1:1로 대응되는 경우로 수정한 것
• 두 집단의 기댓값(평균)이 같은지 여부를 확인하기 위한 검정
• ttest_rel함수를 이용
• 이 검정을 이용하는 경우는, 학생들의 시험 성적이 있는데, 학원을 다니기 전과 학원을 다닌 후 성적의 변화가 있는지, 또는 수면제 복용 전과 복용 후의 수면시간의 평균이 같은지 다른지

# 동일한 집단에게 수면제1과 2를 복용시켰을 때, 수면 시간의 변화
x1=np.array([0.7, -1.6, -0.2, -1.2, -0.1, 3.4, 3.7, 0.8, 0.0, 2.0])
x2=np.array([1.9,0.8, 1.1, 0.1, -0.1, 4.5, 5.5, 1.6, 4.6, 3.4])
r=sp.stats.ttest_rel(x1,x2)
print(r)

등분산 검정

• 2개의 집합의 분산이 같은지 확인
• bartlett, fligner, levene 검정을 이용
• t 검정은 기본적으로 분산이 같다는 전제에서수행

윌콕슨의 부호 순위 검증

• 대응 표본의 차이에 정규 분포를 가정할 수 없는 경우에 사용하는 중앙 값의 차이에 대한 검정
• 일반적으로 차이의 절대 값에 순위를 부여해서 순위 합을 이용하는 방식
• 직접 만들어야 합니다.

# 윌콕슨의 부호 순위 검정
training_rel=pd.read_csv('./data/training_rel.csv')
training_rel.head()
# 데이터 6개 복제
toy_df=training_rel[:6].copy()
# print(toy_df)
# 2개 데이터의 차이를 구하기
toy_df['차']=toy_df['후']-toy_df['전']
# print(toy_df)
# 차의 절대값을 가지고 순위를 구하자.
toy_df['순위']=sp.stats.rankdata(abs(toy_df['차'])).astype(int)
print(toy_df)
# 차이가 음수일 때와 양수일 떄의 순위 합 구하기
r_minus=np.sum((toy_df['차']<0)*toy_df['순위'])
r_plus=np.sum((toy_df['차']>0)*toy_df['순위'])
print(r_minus,r_plus)
# 2개의 값 중에 작은쪽이 검절 통계량 : 8
# 이 값과 임계값(직접 설정한 값)과 비교해서
# 임계값 보다 작은 경우에 귀무 가설이 기각되는 단측검정

분산 분석

• F 통계량
  - 그룹의 수가 2개 이상일 떄 사용
  - 전차 오차로 인한 분산과 그룹 평균의 분산에 대한 비율을 기본으로 합니다.
  - 이 값이 높을 수록 통계적으로 유의미합니다.
  - ols 라는 함수를 이용해서 구할 수 있씁니다.

카이

-범주 별로 관츨 빈도와 기대 빈도의 차이를 통해서 확률 모형이 데이터를 얼마나 잘 설명하는지를 검정

• 관측된 데이터를 대상으로 유의 확률을 적용해서 변수 간의 독립성 여부를 검정
• 웹을 테스트 할 때, A/B 가설을 2개의 처리만 가지고 검정을 수행하는데, 카이 제곱 검정은 여러가지 처리를 한 번에 테스트 할 수 있음
• 변수 간 독립성에 대한 귀무가설이 타당한지를 평가하기 위해서 사용

헤드라인 별 클릭수를 조사해서 동일한 클릭률을 갖는지 확인

헤드라인 A : 14, 헤드라인 -8, 헤드라인 C : 12
클릭x : 988, 988, 988

---

헤드라인 A : 14, 헤드라인 -8, 헤드라인 C : 12
클릭x : 988, 988, 988

• 전체 클릭율을 조사 - 34/3000
• 피어슨 전차 = (관측값-기대값)/기대값의 제곱근
• 카이제곱 통계량 구하기 - 피어슨 잔차들의 제곱합 : 1.666
• 이 값과 재표본 재표본 추출 알고리즘으로 나온 값 ㅣㅂ교 ***
• chisquare라는 함수를 이용해서 검정이 가능
  - 5가지 음료를 각각 선택하도록 만들었을 때, 사람들이 선호하는 음료가 있는지 여부를 검정
  41, 30, 51, 71, 61
  - 유의 수준이 5% 로 카이 제곱 검정 수행: 카이제곱 검정은 T-test와 반대로 해석
  • 유의 수준이 유의 확률보다 크면 귀무가설 식 채택
  • 유의 수준이 유의 확률보다

data=[41,30,51,71,61]
# 카이제곱검정을 수행
print(sp.stats.chisquare(data))
# 유의 수준을 5%로 설정하면 유의 수준이 유의 확률보다 크기에
# 선호도의 차이가 있다라고 해석
# 평균을 가지고 있는 검정과 분산을 가지고 하는 검정은 겨로가 해석을 반대로 합니다.

✔ 기본 선형 대수

선형 대수

• 데이터 분석에 필요한 각종 계산을 돕는 학문
• 대용량 데이터를 포함하는 복잡한 계산 과정을 간단한 수식으로 서술

선형대수에서 사용하는 데이터 유형

• Scala Data
  - 하나의 숫자
• Vector Data
  - 여러 개의 숫자로 이루어진 Data Record, 1차원인데 열이 1개인 2차원ㄴㄴㄴㄴㄴㄴㄴㄴㄴㄴㄴㄴㄴㄴㄴㄴㄴㄴㅇㅇㅇㅇㅇ
• Matrix
  - Vector가 여러 개 모인 것으로 각 Vector의 크기는 같아야 합니다. 2차원 데이ㅓ
• Tensor
  - 동일한 크기의 Martrix가 보인 것, 3차원
  

붓꽃 데이터

• 분류 분석에서 사용하는데, 붓꽃 150개이 데이터를 가지고 꽃받침 길이, 폭, 꽃잎 길이, 꽃잎의 폭을 가지고 3가지로 분류

# 붓꽃 데이터 가져오기
from sklearn.datasets import load_iris\
# 항상 sklearn의 데이터는 data 속성에 feature가 존재하고
# target에 target이 존재합니다.
iris=load_iris()
print(iris)

# 붓꽃 데이터 가져오기
from sklearn.datasets import load_iris\
# 항상 sklearn의 데이터는 data 속성에 feature가 존재하고
# target에 target이 존재합니다.
iris=load_iris()
# print(iris)
# 벡터는 하나의 행
# 가로나 세로 방향으로 여러 개의 스칼라 데이터가 모이면 벡터
# 여러 개의 데이터 묶음에서 하나의 데이터를 선택한 경우를 특징 벡터(Feature Vector)
print(iris.data[0,:])
# 스칼라
print(iris.data[0,0])
# sklearn에서는 벡터를 대입할 때, 열 개수가 1개인 2차원 배열 객체를 대입해야 함
x1=np.array([5.1,3.5,1.4,0.2])
print(x1)
# skearn에서는 위의 경우 아래처럼 생성해서 대입
x1=np.array([[5.1],[3.5],[1.4],[0.2]])
print(x1)

• 2차원 벡터가 들어오더라도 ML에서는 1차원으로 변환해서 사용함

2

행렬

행렬의 전치

• 행과 열을 바꾸는 것
• T라는 속성을 이용해서 구할 수 있고, transpose를 이용해서도 가능
• 2차원인 경우는 T와 transpose()의 결과가 같음
• 3차원인 경우는 transpose

ar=np.array([[1,2,3],[4,5,6]])
print(ar)
print(ar.T)
print(ar.transpose())
# 2차원 배열에서는 t랑 traspose 결과가 같음
# 3차원의 경우는 순서를 정해서 
arr=np.array([[[1,2],[3,4]],[[5,6],[7,8]]])
print(arr)
print(arr.T)
print(arr.transpose(2,1,0))
print(arr.transpose(1,0,2))

대칭 행렬

• 전치 연산을 해서 얻은 행렬과 원래 행렬이 동일한 경우
• 대칭 행렬은 행 과 열의 수가 같은 경우(정방 행렬)에만 가능

희소 행렬 - Sparse Matrix

• 0이 아주 많은 행렬
• 희소 행렬을 생성하고자 하는 경우에는 scipy.sparse 모듈을 이용해서 생성하며, csr_matrix 함수이용
• 희소 행렬을 가지고 밀집 행렬(Dense Matrix)을 만들고자 할 때는 toarray함수를 이용합니다.

• 넥플릭스와 같은 사이트에서 유저와 영화간의 관계를 행렬로 나타내는 경우, 영화의 개수가 많고 실제 유가 본 영화의 개수는 몇 편 안되는데, 이것을 밀집 행렬로 나타내면 메모리 낭비가 발생하기 때문에, 이런 경우는 희소행렬을 사용한다.

from scipy import sparse
# 대각 행렬 (대각선으로만 1이 있는 행렬)을 만드는데
# 기준선은 하나 위로 설정합니다.
ar=np.eye(3,k=1)
print(ar)
# 희소 행렬로 변환
# 희소 행렬은 한눈에 알아보기가 어렵다.]]
sp=sparse.csr_matrix(ar)
print(sp)
# 밀집 행렬로 변환
print(sp.toarray())

벡터와 행렬의 연산

• 차원이 동일하고 차원의 크기가 같은 벡터와 행렬은 산술 연산이 가능한데, 동일한 위치끼리 연산을 수행하는데 차원의 크기가 다르면 연산에 실패한다.
• 스칼라 데이터와 벡터 또는 행렬 그리고 벡터와 행렬의 경우도 산술 연산이 가능한데, 이 경우는 차원이 낮은 쪽의 데이터를 차원이 높은 쪽의 데이터만큼 복제를 해서 수행합니다.
  - 이러한 연산을 브로드캐스팅 연산이라고 합니다.
  - 차원이

# 스칼라, 벡터, 행렬의 산술 연산
# 동일한 차원의 벡터 간의 산술 연산 
# - shape가 같아야 합니다.
x=np.array([10,11,12,13,14])
y=np.array([20,13,22,11,23])
print(x+y)
# 다른 차원의 벡터 간의 산술 연산
# - shape가 다르면 작은 쪽의 shape를 큰 쪽에 맞추어 계산
print(x+5)
# 벡터와 행렬의 계산
# 벡터의 데이터 개수와 행렬의 열의 개수가 같아야 가능합니다.
ar=np.array([1,2,3])
matrix=np.array([[6,7,8],[16,17,18]])
# - shape가 다르면 작은 쪽의 shape를 큰 쪽에 맞추어 계산
print(ar+matrix)

벡터의 내적 - dot product

• 벡터의 곱인데 서로 다른 두 벡터의 행과 열의 값을 곱해서 모두 더한 값
• 연산이 가능하려면, 행과 열이 교차해서 개수가 같아야 합니다.
• numpy dot 함수나 @연산자를 이용해도 됩니다.
• 일차원 배열의 경우, 전치를 하지 않아도 됩니다.
• 이차원 이상의 겨웅, 반드시 연산이 가능한 형태로 만들어서 수행해야 합니다.

# 벡터의 내적
x=np.array([1,2,3])
y=np.array([4,5,6])
# 일차원 배열은 전치를 하지 않아도 내적 계산 가능
print(np.dot(x,y))
print(x@y)
# 벡터의 내적은 행과 열의 개수가 크로스 방향으로 같을 때 가능함
print(x.T@y)
x=np.array([[1],[2],[3]])
y=np.array([[4],[5],[6]])
# print(np.dot(x,y)) # 오류
# 내적을 할 때는 한 쪽을 전치해줘야 한다.
print(np.dot(x.T, y))

내적을 사용하는 대표적인 경우는 가중치 적용이다.

• 가중 합이나 가중 평균을 구하기

score=np.array([90,70,85])
# 단순한 평균
print(score.mean())
# 학점이 3,2,3 학점일 때, 그냥 평균으로 처리해야 할까?
# 이럴 때 쓰는 것이 가중합이다.
# 가중 평균 구하기
su=np.array([3,2,3])
print(score@su / 8)

유사도 계산

• 유사도는 두 벡터가 닮은 정도를 정량적으로 나타낸 값이다.
• 두 벡터가 비슷한 경우에는 유사도가 커지고, 비슷하지 않은 경우에는 유사도가 낮아짐
• 내적을 이용하면 코사인 유사도를 계산할 수 있음

# 이미지의 유사도 계산
from sklearn.datasets import load_digits
import matplotlib.gridspec as GridSpec
digits=load_digits()
# print(digits)
# 이미지 가져오기
# 숫자 0
d1=digits.images[0]
d2=digits.images[10]
# 숫자 1
d3=digits.images[1]
d4=digits.images[11]
# 이미지 데이터 - 2차원이지만 이를 일차원으로 만들자.
v1=d1.reshape(64,1)
v2=d2.reshape(64,1)
v3=d3.reshape(64,1)
v4=d4.reshape(64,1)
plt.figure(figsize=(9,9))
gs=gridspec.GridSpec(1,8, height_ratios=[1], width_ratios=[9,1,9,1,9,1,9,1])
for i in range(4):
    plt.subplot(gs[2*i])
    # 원본 이미지 출력
    plt.imshow(eval("d"+str(i+1)),aspect=1,
               interpolation='nearest', cmap=plt.cm.bone_r)
    plt.grid(False)
    plt.xticks([])
    plt.yticks([])
    plt.title("image {}".format(i+1))
    plt.subplot(gs[2*i+1])
    plt.imshow(eval("v"+str(i+1)),aspect=0.25,
               interpolation='nearest', cmap=plt.cm.bone_r)
    plt.grid(False)
    plt.xticks([])
    plt.yticks([])
plt.show()
# 유사도 계산하기
# 1차원으로 하면 값이 하나로 나옴
print(d1.T@d2)
print(v1.T@v2) # 내적이 가장 큼
print(v1.T@v3)
print(v1.T@v4)
print('==============')
print(v3.T@v1)
print(v3.T@v2)
print(v3.T@v4) # 내적이 가장 큼

선형 회귀 모형에 활용

• 회귀 모형은 독립 변수(요인 변수 - x)를 가지고 종속 변수(y)를 예측하는 모형
• 선형 회귀 모형은 1차원 방정식의 형태로 회귀모형을 만드는 것
• 가중치1 독립변수1 + 가중치2 독립변수2 ...+절편(intercept,상수)=종속변수
  - 이를 선형 회귀 라고 합니다.
  - 이 모형은 벡터의 내적으로 표현이 가능하다.
• 비선형은 독립변수의 차수가 2 이상 나오는 경우이다.

제곱합

• 각각의 데이터를 제곱한 뒤 모두 더한 값(sum of squares)

행렬의 곱셈

• 앞의 행렬 행과 뒤의 행렬의 열의 내적을 가지고 행렬로 리턴
• 행렬이 곱이 성립하려면, 앞 행렬의 행의 수와 뒤 행렬의 열의 수가 같아야 합니다.
• np.dot에 차원이 1을 초과한 행렬을 2개 대입하면 행렬의 곱

a=np.array([[1,2,3],[4,5,6]]) #2x3
b=np.array([[1,2],[3,4],[5,6]]) # 3x2
# 결과물은 2x2
print(np.dot(a,b))

행렬과 단위 행렬을 곱셈하면 자기 자신이 리턴됩니다.

• 단위 행렬(항등 행렬)
  - 주 대각선 방향으로만 1을 가지고 있는 행렬

ar=np.array([[1,2,3],[4,5,6],[7,8,9]])
i=np.eye(3)
print(ar@i)

이미지를 가지고 행렬과 벡터의 곱을 구하면, 이미지 모핑(합성) 효과를 얻을 수 있다.

# 행렬과 벡터의 곱셈을 이용한 이미지 모핑(Morphing)
#얼굴 이미지 데이터 가져오기
from sklearn.datasets import fetch_olivetti_faces
faces=fetch_olivetti_faces()
f,ax=plt.subplots(1,3)
new_face=0.65*faces.images[13]+0.35*faces.images[26]
ax[0].imshow(faces.images[13],cmap=plt.cm.bone)
ax[0].grid(False)
ax[0].set_xticks([])
ax[0].set_yticks([])
ax[0].set_title("image 1")
ax[1].imshow(faces.images[26],cmap=plt.cm.bone)
ax[1].grid(False)
ax[1].set_xticks([])
ax[1].set_yticks([])
ax[1].set_title("image 2")
ax[2].imshow(new_face,cmap=plt.cm.bone)
ax[2].grid(False)
ax[2].set_xticks([])
ax[2].set_yticks([])
ax[2].set_title("image 3")
plt.show()

잔차 (residual)

• 예측치와 실제 데이터 사이의 오차를 의미함
• 모든 독립 변수 벡터에 대해서 잔차를 구하면, 잔차 벡터가 만들어집니다.

잔차 제곱합

• 잔차 벡터의 각 원소를 제곱하고 더한 것을 잔차 제곱합이라고 합니다.(Residual Sum of Squares)
• 회귀 분석 모델의 성능 평가 지표로 사용합니다.

# 잔차 제곱합 구하기
x=np.array([1,2,3])
A=np.arange(1,10).reshape(3,3)
# 잔차 제곱합
print(x.T@A@x)

이차 형식

• 벡터의 이차 형식이란, 어떤 벡터와 정방행렬이 (행벡터 @ 정방행렬 @ 열벡터) 형태로 존재하는 것

대각합

• 정방행렬에서 주 대각선 데이터의 합
• numpy.trace 함수를 이용해서 구할 수 있음

vector=np.eye(3)
print(vector)
print(np.trace(vector))

행렬식

• 연립 선형 방정식의 성질을 결정하기 위해서 정의
• numpy.linalg.det함수를 이용해서 행렬식으로 계산할 수 있습니다.

# 행렬식
mat=np.array([[1,2],[3,4]])
print(np.linalg.det(mat))

역행렬

• 행렬의 곱이 단위행렬이 되도록 해주는 정방행렬
• 역행렬은 무조건 존재하지는 않고, 특정 조건을 만족하는 경우에만 존재합니다.
• 역행렬이 존재하는 경우는 가역 행렬(Invertible Matrix, Regular Matrix)이라 합니다.
• 역행렬이 존재하지 않는 경우는, 비가역 행렬(non-invertible matrix, singular matrix - 특이행렬)이라고 합니다.
• 역행렬이 존재하지 않을려면, 주 대각선의 합에서 반대편 대각선의 합이 일치하면 됩니다.
• [[a,b],[c,d]] 행렬의 역행렬 구하는 공식 : (1/(ad-bc) 곱셈 [[d-b],[-c,a]])
• numpy.linalg.inv 함수로 역행렬을 구할 수 있습니다.

# 역행렬 구하기
a=np.array([[1,2],[3,4]])
inv=np.linalg.inv(a)
print(inv)
print(a.T@inv)

벡터의 합

• 두 벡터를 이웃으로 하는 변을 가지는 평행 사변형의 대각선 벡터
• 더하고자 하는 벡터의 끝점으로 평행 이동해서 가리키는 점의 위치

벡터의 차

• 한쪽 벡터의 끝점에서 다른 벡터의 끝 점으로 연결

word2vec

• 단어를 공간에서 점이나 벡터로 표현
• word2vec으로 만들어진 벡터는 단어의 의미에 따라 평행 사변형 관계를 가질 수 있음
• 한국과 서울의 관계를 가지고, 웰링턴과 관계가 있는 단어는?
• 뉴질랜드= 웰링턴+(한국-서울)

유클리드 거리

• 두 벡터가 가리키는 점 사이의 거리가 유클리드 거리
• 유클리드 거리가 벡터의 차

✔ Machine Learning

인공지능

지능

• 문제를 해결할 수 있는 능력

인공지능

• 지능 작업을 수행할 수 있는 기계의 능력

인공지능 구현 방법

• 지식공학 $\rarr$ 전문가 시스템, 특정 분야의 전문가나 장인들이 학문을 연구하거나 오랜 실무 경험으로 터득한 지식을 컴퓨터에 제공
• Data와 Program(Algorithm)을 입력하고 컴퓨터가 Output을 만들어내는 방식

규칙과 데이터 $\rarr$ 해답

• Machine Learning - 컴퓨터가 데이터로부터 학습
• Data와 Output을 컴퓨터에게 제공하고 Algorithm을 컴퓨터가 만들어 내는 것
• 데이터와 해답 $\rarr$ 규칙

인공지능 > 머신러닝 > 딥러닝

Machine Learning

개요

• 데이터를 가지고 학습하도록 컴퓨터를 프로그래밍 하는 것

필요 요소

• 입력 데이터 포인트
  - 음성 인식이라면 음성 파일, 이미지 태깅을 하고자 하면 이미지
• 기대 출력
  - 음성 인식 경우는 음성을 가지고 만들어 낸 텍스트, 이미지 태깅이라면 종류에 대한 태그
• 알고리즘의 성능을 측정하는 방법
  - 알고리즘의 현재 출력과 기대 출력 간의 차이를 결정하기 위해서 필요한데, 이 측정 값은 알고리즘의 작동 방식을 교정하기 위한 신호로 다시 피드백되는데, 이런 수정 단계가 학습임
  

흰색과 빨간색을 분류하는 문제의 경우

• 필요 요소
  - 입력 데이터는 데이터 좌표
  - 기대 출력은 색상
  - 성능 평가 지표는 제대로 판정한 데이터의 비율
• 머신러닝 알고리즘은 주어진 작업을 위해서 데이터를 더 유용한 표현으로 바꾸는 변환 작업을 자동으로 수행하는데, 이러한 변환 작업은 좌표 변환일 수 도 있고, 선형 투형(정보를 제거), 이동, 비선형 연산 등이 있습니다.
  - 머신 러닝 알고리즘은 변환을 찾기 위한 창의력은 없고 가설 공간이라 부르는 정의된 연산의 모음들을 자세히 조사하는 것 뿐

---

머신러닝은 가능성 있는 공간을 사전에 정의하고 피드백 신호의 도움을 받아서 입력 데이터에 대한 유용한 변환을 찾는 것입니다.

머신러닝을 사용하는 이유

• 데이터가 수시로 변하기 때문입니다.
  - 전통적인 방식은 데이터에 변형이 가해지거나 새로운 데이터가 추가된다면 프로그램을 다시 만들어야 하지만, 머신 러닝은 학습만 다시 수행하도록 하면 됩니다.
• 전통적인 방식으로는 너무 복잡하거나 알고리즘이 없는 문제를 해결하기 위해서

머신 러닝의 역사

• 확률적 모델링
  - 통계학 이론을 데이터 분석에 응용한 것
  - 나이브 베이즈 알고리즘을 많이 사용했는데, 입력 데이터의 특성이 모두 독립적이라고 가정하고 베이즈 정리를 적용하는 분류 알고리즘
  - 컴퓨터가 나오기 전에 만들어진 알고리즘
  - 나이브 베이즈를 적용한 분류 알고리즘으로 현재도 많이 사용되는 알고리즘은 로지스틱 회귀 알고리즘이 있습니다.
  - 분류 모델을 만들 때, 가장 먼저 적용해보는 모델입니다.
• 신경망(1950s 등장)
  - 일찍 만들어졌지만, 대규모 신경망 훈련을 하는 효과적인 방법이 없었으며, xor 문제도 존재함.
  - 나중에 경사 하강법 알고리즘을 사용해서 대규모 신경망을 훈련시킬 수 있게 됨
  - 신경망을 이용한 첫 번째 애플리케이션으로는 1989년 bell 연구소 얀 르쿤이 CNN을 이용해서 만든 손 글씨 이미지 분류인 mnist 이다.
  
• 커널 방법
  - Support Vector Machine이 유명
  - 분류 문제를 해결하기 위해서 2개의 다른 범주에 속한 데이터 포인트 그룹 사이에 결정 경계를 만들어서 해결함
  - 결정 경계를 만들고 각 데이터와의 거리를 계산해서 학습
  - 이 방식을 사용하려면 데이터를 잘 가공해야 합니다.
• decision tree, random forest, gradient boosting
  - 결정트리는 플로 차트 같은 모양으로 입력에 대해 출력을 예측
  - random forest는 여러 개의 결정 트리를 만들고 그 출력을 앙상블하는 방식
  - gradient boosting 알고리즘은 결정 트리를 이용하는데, 결정 트리를 만들고 새로운 결정 트리를 만들 떄는 이전 결정 트리에서 잘못 판단된 데이터에 가중치를 부여해서 생성하는 방식
  - 딥러닝을 제외하고는 가장 우수한 성능을 발휘하는 것이 gradient boosting
• 다시 신경망으로

알고리즘을 분류

• 레이블의 존재 여부에 따른 분류
  - 지도학습, 비지도학습, 준지도학습, 강화학습
• 실시간으로 점진적인 학습이 가능한지 여부
  - 온라인 학습과 배치 학습
• 사례 기반 학습(알고 있는 값과 새로 만들어진 값을 비교하는 것) 과 모델 기반 학습(패턴을 발견해서 예측 모델을 만드는 것)

지도 학습

• 레이블이 존재하는 경우, 수행하는 머신러닝
• 데이터가 입력과 출력이 쌍으로 제공되어야 한다.
• 분류
  - 출력이 이산적이 값이면 Classification(분류)
  - 출력이 analog(연속적인) 값이면 REgression(회귀)
  - 출력이 확률이면 Deep Learning
• 단점
  - 사용할 수 있는 데이터에 한계가 있음
  - 데이터를 생성하는데 비용이 많이 소모됨
• 주요 알고리즘
  - KNN - k 최근접 이웃
  - Linear Regression - 선형 회귀
  - Logistic Regression - 로지스틱 회귀(분류임)
  - Support Vector Machine
  - Decision Tree
  - Random Forest
  - Neural Network
  

비지도 학습

• 레이블이 존재하지 않는 학습으로 입력 데이터만 존재
• 클러스터링(군집)과 차원 축소(여러 차원의 데이터를 저차원으로 축소)가 대표적이며 이상치 탐지나 연관 규칙 학습 등에 활용
• 지도 학습에 비해서 하습하기가 어려움
• 주요 알고리즘(군집)
  - K-means
  - DBSCAN
  - HCA(계층 군집 분석)
  - 이상치 탐지 및 특이치 탐지
  - one-class SVM
  - isolation forest
• 주요 알고리즘(시각화 & 차원 축소)
  - PCA(주성분 분석)
  - 커널 PCA
  - LLE(지역적 선형 임베딩)
  - t-SNE
• 주요 알고리즘(연관 규칙 학습)
  - Apriori
  - Eclat
  

준지도 학습

• 레이블이 일부분만 존재하는 경우

강화학습

• 최종 결과가 바로 주어지지 않고, 시간이 지나서 주어지는 학습
  - 학습하는 시스템을 Agent라고 하고 Environment를 관찰해서 ACtion을 실행하고 그 결과로 Reward나 부정적인 보상에 해당하는 Penalty를 받는 방식으로 시간이 지나면서 보상이 큰쪽으로 학습해나가는 것

배치학습과 온라인 학습

• 배치학습
  - 데이터를 모아서 한꺼번에 학습
  - 시스템이 점진적으로 학습할 수 없는 상황에서 사용
  - 오프라인에서 작업
  - 주기가 존재함
  - 시스템이 빠르게 변화하는 데이터에 적응해야 하는 경우에는 사용하기가 어려움
• 온라인 학습
  - 데이터를 작은 단위로 쪼개서 학습을 연속해나가는 방식
  - 시스템의 성능이 좋지 않아도 사용이 가능합니다.
  - 학습률(데이터에 얼마나 빠르게 적응할 것인지 여부)을 선택하는 것이 어려움
  - 학습률 : 얼마나 자주 학습을 할 것이냐
  

일반화 여부에 따른 분류

• 사례 기반 학습
  - 단순히 기억하는 것
  - 현재 존재하는 데이터를 가지고 결과를 확인만 하는 형태
• 모델 기반 학습
  - 현재 데이터를 가지고 모델을 만들어서 새로운 데이터에 대해서 예측을 하는 형태의 학습