수업 39일차

✔ 다변량 탐색

• 명목 척도
  - 단순한 구분이 목적
  - 성별 : 남/여 구분이 목적
• 순서 척도
  - 구분을 하고, 데이터의 순서가 의미를 갖는 구조
  - 학력 : 고졸, 대졸, 대학원졸 으로 구분(의미 O)
• 등급 척도
  - 각 데이터의 구분이 일정한 비율
  - 학년이나 만족도 : 학년은 일정한 비율을 가지지만, 산술 연산을 하지 않음
• 비율 척도
  - 값과 값 사이에 다른 값이 존재하는 구조 (아날로그 성격)
  - 몸무게와 온도

범주형과 범주형의 데이터의 분포 확인

• 데이터가 범주형이어서 그래프로 표현하기가 쉽지 않다.

# 분할표 사용 - 범주형과 범주형 데이터의 분포를 확인
lc_loans=pd.read_csv('./data/lc_loans.csv')
# lc_loans.head()
# grade 별로 status의 개수를 확인하고 싶다.
crosstab=lc_loans.pivot_table(index='grade', columns='status',
                             aggfunc=lambda x:len(x), margins=True)
# print(crosstab)
# margin 은 뷰 프로그래밍에서 컨텐츠와 컨텐츠 사이의 여백이다.
# 하지만, 통계에서는 전체에 관련된 집계 데이터를 의미합니다.
# 맨 밑 행 All 을 빼고 비율을 표시해보자.
# grade의 비율을 표시하기 위한 교차 분할 표
df=crosstab.copy().loc['A':'G'] #복제
df.loc[:,'Charged Off':'Late']=df.loc[:,'Charged Off':'Late'].div(df['All'],axis=0)
df['All']=df['All']/sum(df['All'])
print(df)

범주형과 수치형 데이터의 분포 확인

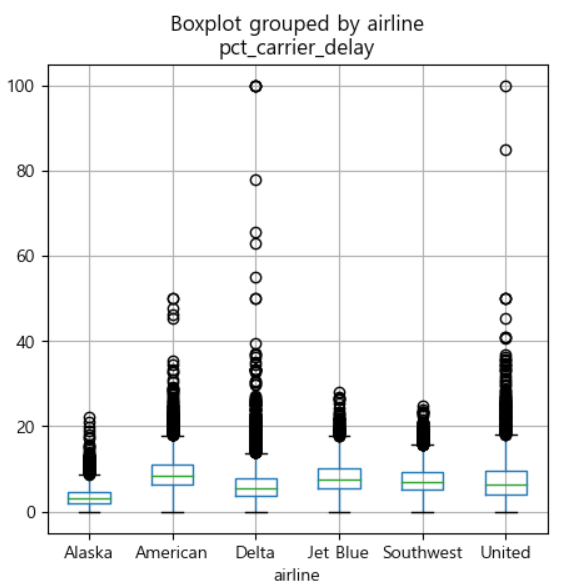
• boxplot 이용
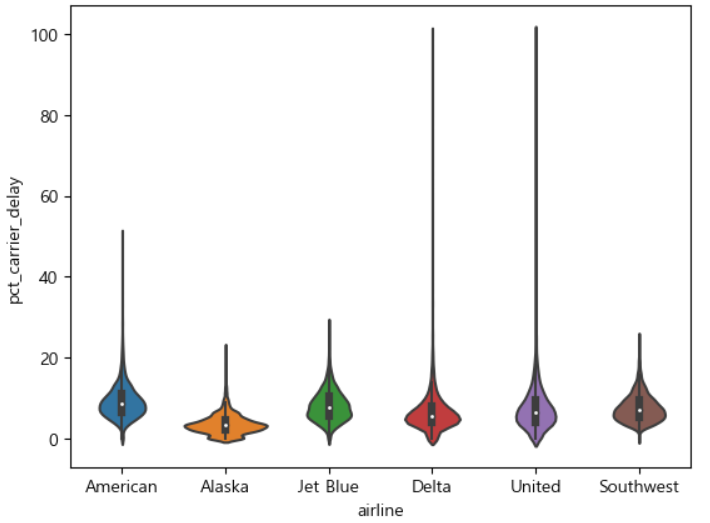
  - 데이터의 범위를 나타내는 것에는 효과적이지만, 특정 데이터의 분포까지 확인하기는 어렵다.
• violinplot인 swamplot 등을 이용
  - 데이터의 분포까지 표현 가능
  - 기본 차트가 아니기에 seaborn이나 다른 라이브러리에 존재 (matplotlib X)
  

# 범주형과 수치형 데이터 분포 확인
airline_stats=pd.read_csv('./data/airline_stats.csv')
airline_stats.head()
# 항공사별로 케리어가 딜레이되는 것을 확인해볼까?
ax=airline_stats.boxplot(by='airline', column='pct_carrier_delay',
                        figsize=(5,5))
# 값의 범위를 확인하기는 좋지만, 분포를 파악하기에는 약간 어려움
plt.show()

---

import seaborn as sns
sns.violinplot(data=airline_stats,x='airline', y='pct_carrier_delay')
plt.show()

조건화

• 교차분할표나 산점도, 육각형 구간 등의 차트를 특정 변수의 값으로 비교하기 위한 것

✔ 확률

확률

• 현실에서 해결하고자 하는 문제가 있는 경우, 이 문제가 어떤 답을 가질 수 있고, 그 답의 신뢰성이 얼마나 되는지 정량적인 방법을 제시

개념

• 시행
  - 조작
• 확률 표본
  - 시행으로 발생할 수 있는 하나의 현상 또는 선택될 수 있는 하나의 경우
• 표본 공간
  - 가능한 모든 표본의 집합
• 수학적 확률
  - 표본 공간에서 표본이 발생할 가능성
• 대수적 확률
  - 몇 번 반복해서 얻을 수 있는 비율을 통계적 확률이라 하며, 시행을 많이 하면 통계적 확률은 수학적 확률과 비슷해진다는 것
• 수학적 확률을 빈도주의 관점이라고 하고, 베이지안 관점은 수학적 확률의 신뢰도를 의미합니다.

확률 관련 패키지

• pgmpy 패키지를 이용함

베이즈 정리

검사 시약 문제

• 제약사에서 환자가 특정한 병에 걸렸는지 확인하는 시약을 만들었는데, 그 병에 걸린 환자에게 시약을 테스트한 결과가 99%의 정확도를 나타냄
• 일반적인 사람이 이 시약을 테스트한 결과 양성으로 나타난 경우, 실제 이 병에 걸렸을 확률은?
• 이 경우에는 병에 걸릴 확률이 얼마인지를 알아야 합니다.
  - 이 병은 전체 인구 중 걸린 사람이 0.2% 입니다.
• 이 병에 걸리지 않은 사람에게 시약을 테스트 했을 때, 양성으로 나온 확률을 알아야 합니다.
  - 5%
• 문제를 해결해보자.
  - (0.99*0.002)/((0.99*0.002)+(0.05*(1-0.002)) = 0.038
  - pgmpy 의 BayesianModel 클래스를 이용해서 계산이 가능합니다.
• 이 정리가 머신러닝에서 분류에서 사용됩니다.
• 감성분류에서도 사용합니다.
• BayesianModel의 TabluarCPD(확률 변수의 이름 문자열, 경우의 수, 조건부 확률 배열:합치면1)

# 병에 걸릴 확률과 병에 걸리지 않을 확률을 생성
from pgmpy.factors.discrete import TabularCPD
cpd_X=TabularCPD('X',2,[[0.998],[0.002]])
print(cpd_X)
# 진단 시약의 판단 여부를 대입해서 확률 모형을 생성
# 정상인 경우 정산으로 판단 95% 잘못 판단 5%
# 병에 걸린 경우, 병에 걸리지 않았다고 판단 1%, 양성판단 99%
# cpd_X 데이터 순서와 맞게 만들자.
cpd_Y_on_X=TabularCPD('Y',2,np.array([[0.95,0.01],[0.05,0.99]]),
                     evidence=['X'], evidence_card=[2])
print(cpd_Y_on_X)
# 모델 생성
from pgmpy.models import BayesianModel
model=BayesianModel([('X','Y')])
model.add_cpds(cpd_X,cpd_Y_on_X)
# 모델이 정상적으로 만들어졌는지 확인
# print(model.check_model())
# 양성으로 나왔을 때의 확률
from pgmpy.inference import VariableElimination
inference=VariableElimination(model)
print(inference.query(['X'],evidence={'Y':1}))
# 음성으로 나왔을 때의 확률
print(inference.query(['X'],evidence={'Y':0}))

확률 분포

• 확률적 데이터를 살펴보면, 어떤 값은 자주 등장하고, 어떤 값은 드물게 나오거나 나오지 않는데, 어떤 값이 자주 나오고 어떤 값이 자주 나오지 않는지를 나타내는 정보
• 봉우리가 한 개 이면, 단봉(uni-modal)이라 하고, 봉우리가 여러개이면 다봉(multi-modal) 분포라고 합니다.
• 대표값
  - 평균, 중앙값, 최빈값
• 대칭 분포
  - 분포가 표본 평균을 중심으로 좌우 대칭인 경우, 중앙값은 평균과 일치
  - 분포가 대칭 분포이면서 하나의 최고값 만을 갖는 단봉 분포이면, 평균과 최빈값은 일치
  - 이 데이터에 비대칭을 만드는 데이터가 추가된다면, 평균이 가장 크게 영향을 받고, 최빈값이 가장 적게 영향을 받음
• 분포 추정 방법으로 분산과 표준편차 이용 가능
• 표본 비대칭도(왜도 - skewness)
  - 평균과 데이터의 차이를 3제곱한 값
  - 비대칭도가 0이면 대칭분포
  - 비대칭도가 음수이면 평균을 기준으로 왼쪽에 있는 값이 더 많은 것이고, 양수이면 평균을 기준으로 오른쪽에 있는 값이 더 많은 경우
• 표본 첨도(첨도 - kurtosis)
  - 평균과 데이터의 차이를 4제곱한 값
  - 데이터가 중앙에 몰려있는 정도를 비교할 때 사용
  - 첨도가 양수이면 중앙에 데이터가 몰린 것이 정규분포보다 심한 경우
  - 첨도가 음수이면 정규분포보다 중앙에 데이터가 몰리는 것이 적은 경우
• 평균을 1차 모멘트, 분산이 2차 모멘트, 비대칭도 3차 모멘트, 첨도가 4차 모멘트 라고 합니다.

확률 분포 모형

• 확률 질량 함수
  - 각각의 사건이 나올 확률을 그린 그래프
• 누적 확률 함수
  - 각각의 사건이 나올 확률을 누적시켜서 그린 그래프

베르누이 분포

• 베르누이 시행
  - 결과가 두 가지 중 하나로만 나오는 실험이나 시행
• 베르누이 확률 변수
  - 베르누이 확률 변수의 표본 값은 보통 0 또는 1로 표현하지만 1또는 -1로 표현하기도 합니다.
  - 두 값 중 하나의 값만 가질 수 있기에 이산 확률 변수라고 합니다.(이산 : 끊어지는, digital화된)
• scipy의 stats 서브 패키지의 bernoulli라는 클래스를 이용해서 구현
  - p라는 인수를 가지고 분포의 모수를 설정
  - 확률 질량 함수는 pmf()로 계산
  - 표본 값을 무작위로 생성하려면 rvs() 이용
  - 기술 통계값 확인은 describe()

이항 분포

• 베르누이 시행을 N 번 반복하는 경우에 성공한 횟수를 분포로 만든 것
• 샘플 데이터가 1개이면, 베르누이 분포가 되는 것이고, 여러 번이면 이항 분포이다.
• scipy의 stats 서브 패키지의 binom이라는 클래스를 이용해서 구현합니다.
• 이항 분포를 활요하는 분야는 분류 분석에서 클래스가 2개인 경우, 어떤 클래스로 구분할 지에 이용

카테고리 분포

• 다중 분류 문제에 사용하는 분포
• 나올 수 있는 경우가 3가지 이상인 경우에 활용
• 카테고리 분포를 여러 번 수행하면 다항 분포라고 합니다.

정규 분포

• Gaussian Normal Distribution
• 자연 현상에서 나타나는 숫자를 확률 모형으로 모형화 할 때 가장 많이 사용되는 모형
• 데이터들이 평균을 기준으로 좌 우 대칭형으로 분포되어 있는 형태
• 평균 값을 기준으로 표준 편차 1배 안에 약 68%정도의 데이터가 2배 안에 95% 정도의 데이터가 분포된 경우
• 어떤 분포가 정규 분포와 얼마나 가까운지 그림을 그릴 수 있는데, 이 그림을 QQ Plot이라고 합니다.

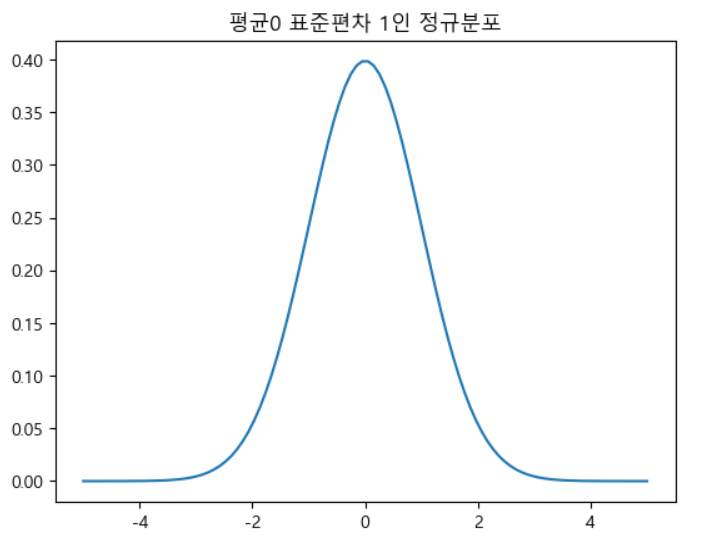
import seaborn as sns
import scipy as sp
import scipy.stats
# 정규 분포 만들기
# 항상 평균, 표준편차가 필요함
mu=0 # 평균 0
std=1 # 표준편차 1
# 정규분포 객체 생성
rv=sp.stats.norm(mu,std)
# 샘플 데이터 100개 생성
# 대칭이 맞아야 하니 범위는 -5 ~ 5
xx=np.linspace(-5,5,100)
# 그려보자
plt.plot(xx,rv.pdf(xx))
plt.title('평균0 표준편차 1인 정규분포')
plt.show()

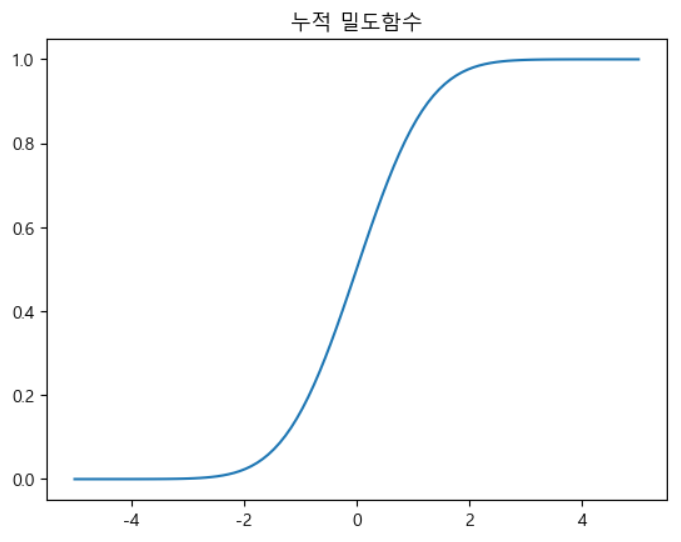
# data sampling
x=rv.rvs(100)
print(x)
plt.plot(xx,rv.cdf(xx))
plt.title('누적 밀도함수')
plt.show()

주식의 수익률이 정규 분포를 따르는지 확인하기

• pandas_datareader 패키지의 data 모듈은 웹의 데이터를 가져와서 DataFrame을 만들어주는 모듈
• 설치 : conda install pandas-datareader 오류나면 datareader=0.5.0
• 매개변수
  - name : 가져올 데이터 목록
  - data_source : 가져올 url
  - start : 시작 날짜
  - end : 종료 날짜
  - retry_count : 재시도 횟수
  - pause : 데이터가 많은 경우 중간에 쉬는 시간
  - session : 세션 사용 여부
  - api_key

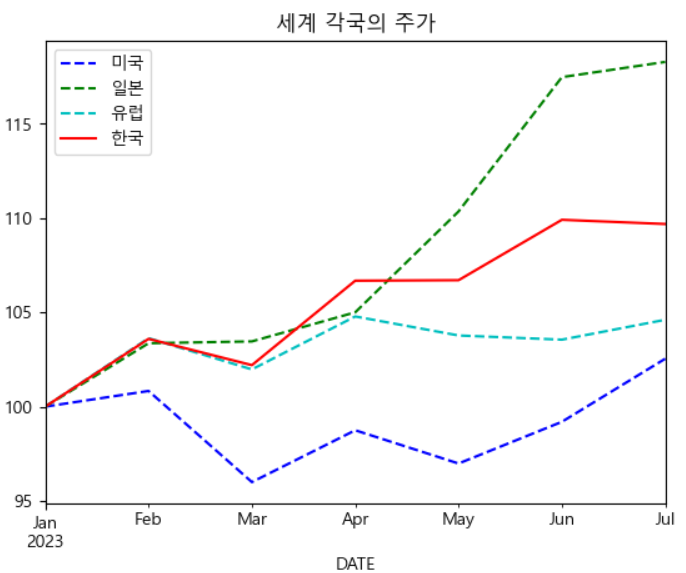
import pandas_datareader.data as web
import datetime
# 날짜 설정
start=datetime.datetime(2023,1,1)
end=datetime.datetime(2023,8,22)
# 가져올 국가의 주가 지수 코드
symbols=['SPASTT01USM661N','SPASTT01JPM661N','SPASTT01EZM661N', 'SPASTT01KRM661N']
data=pd.DataFrame()
for symbol in symbols:
    data[symbol]=web.DataReader(symbol, data_source='fred',
                            start=start, end=end)[symbol]
print(data.head())
data.columns=['미국','일본','유럽','한국']
data=data/data.iloc[0]*100
styles=['b--','g--','c--','r-']
data.plot(style=styles)
plt.title('세계 각국의 주가')
plt.show()

• 나스닥 지수

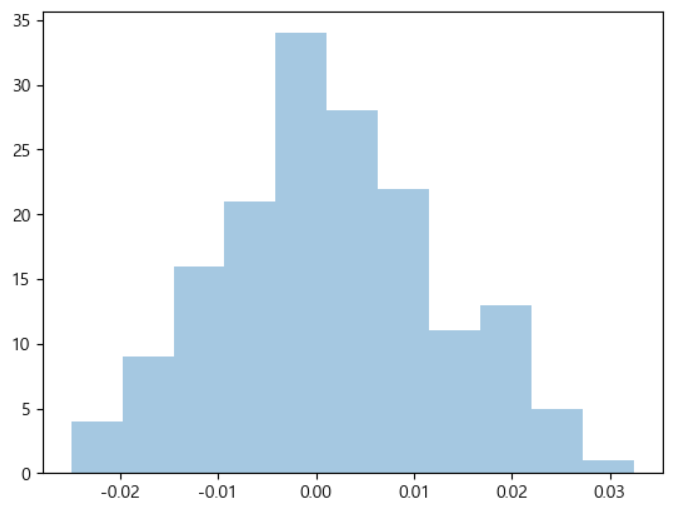
data=pd.DataFrame()
symbol='NASDAQCOM'
data[symbol]=web.DataReader(symbol, data_source='fred',
                            start=start, end=end)[symbol]
data.plot(legend=False)
plt.title('나스닥 지수')
plt.show()
# 일자별 차이
daily_returns=data.pct_change().dropna()
# print(daily_returns)
# 일자별 차이를 그래프로 출력
# 정규분포와 유사한 그래프가 그려짐
sns.distplot(daily_returns,kde=False)
plt.show()

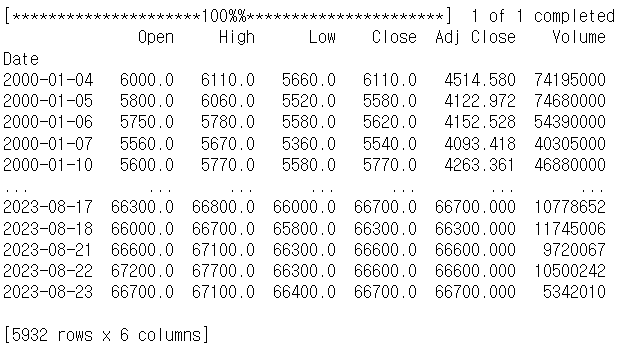
# 특정한 회사 주가 가져오기
import pandas as pd
import pandas_datareader.data as web
import yfinance as yfin
yfin.pdr_override()
# 주식 코드만 바꾸면 다 확인 가능
samsung=web.get_data_yahoo("005930.KS")
print(samsung)

정규 분포와 선형 회귀 모델

• 선형 회귀 모형에서 잡음을 모형화하는데 정규 분포를 사용합니다.
• 잔차
  - 예측 값과 실제 값의 차이
• 잡음(noise)
  - 속성이 여러 개인 경우, 결과에 영향력이 적은 변수들의 영향을 하나로 합친 것

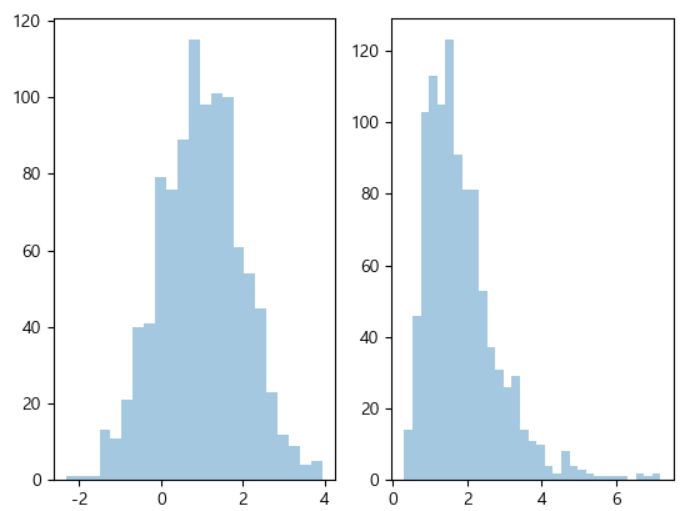
로그 정규 분포

• 데이터에 로그를 한 값이 정규 분포를 따르는 경우
• 주가가 로그 정규 분포
• 데이터 자체는 한쪽으로 치우치는 것처럼 보이는 형태

# 정규 분포와 로그 정규 분포 모형 비교
mu=1
rv=sp.stats.norm(loc=mu)
x1=rv.rvs(1000)
s=0.5
x2=np.exp(s*x1)
fig ,ax=plt.subplots(1,2)
sns.distplot(x1,kde=False,ax=ax[0])# 정규 분포
sns.distplot(x2,kde=False,ax=ax[1])# 로그 정규 분포
plt.show()

중심 극한 정리

• 모집단이 정규 분포가 아니더라도, 표본 크기가 충분하고 데이터가 정규성을 크게 이탈하지 않는다면, 여러 표본에서 추출한 평균은 종 모양의 정규곡선을 따른다.
• 머신러닝의 모델은, 계속해서 학습을 해나가야 정확한 모델에 가까워지게 됩니다.

균일 분포

• 모든 경우가 동일한 확률로 발생하는 분포

스튜던트 t 분포

• 현실의 데이터들은 정규분포와 유사하지만, 양 끝단의 비중이 정규 분포에 비해서 더 큰 데이터들을 발견할 수 있는데, 이런 형태의 분포를 스튜던트 t분포라고 합니다.
• 이렇게 거의 발생할 수 없는 극단의 사건을 Black Swan이라고 합니다.
• 정규분포를 따르는 확률 변수 X의 N개의 표본의 합은 표본 분산으로 정규화를 하면, 스튜던트 t 분포를 따른다.

카이 제곱 분포(chi squared)

• 정규 분포를 따르는 표본의 합 대신에 제곱을 한 값의 합의 분포를 카이 제곱 분포라고 합니다.

푸아송 분포

• 일반적으로 시간 간격에서 이벤트가 발생한 횟수를 모델링 할 때 사용
• 일정 기간 동안 웹 사이트에서 방문한 사용자의 수는 푸아송 프로세스로 간주하고 5초동안 서버에 도착한 인터넷 트래픽을 95% 확률로 완벽하게 처리하는데 필요한 용량은 얼마인가?

지수 분포

• 사건이 서로 독립적일 때, 일정 시간 동안 발생하는 사건의 수가 푸아송 분포이고, 다음 사건이 일어날 때 까지 대기 시간이 지수 분포를 따른다고 함
• 웹 사이트를 방문하고 다음 방문이 일어나기 까지의 시간 또는 톨게이트에 자동차가 도착하는 시간 사이 등을 예측할 때 이용함

감마 분포

• 푸아송 사건이 일정한 횟수까지 발생할때 까지의 대기 시간을 나타내는 분포

베이불 분포

• 많은 경우에 사건 발생률ㄹ은 시간에 따라 일정하지 않은데, 이런 경우에는 상대적으로 일정한 구간을 세분화해서 분석을 해야 합니다.
• 항공기 사고나 공장 시스템에서 고장이 발생하는 사건을 예측하는데 사용

• 포아송 분포

# 포아송 분포
data_poisson=sp.stats.poisson.rvs(mu=3, size=1000)
ax=sns.distplot(data_poisson, bins=30, color='magenta', kde=False)
plt.show()

✔ 샘플링

전수 조사와 표본 조사

• 전수 조사
  - 모집단 내의 모든 데이터를 가지고 조사하는 방법
• 표본 조사
  - 모집단으로부터 추출된 표본을 대상으로 분석을 실시
  

용어

• sample
  - 큰 데이터 집단으로부터 얻어낸 부분 집합
• population
  - 모집단, 데이터 집합을 구성하는 전체
• N
  - 모집단의 크기
• Random Sampling - 랜덤 표본 추출
  - 무작위 표본을 추출하는 것
• Stratified Sampling - 층화 표본 추출
  - 모집단을 층으로 나눈 뒤, 각 층에서 무작위로 추출하는 것
• Sample Bias - 표본 편향
  - 모집단을 잘못 대표하는 표본
• 표준 오차
  - 통계에 대한 표본 분포의 변동성을 의미하는 지표
  - 표준편차 / 표본크기의 제곱근
• 표준 오차를 2배로 줄일려면 표본 크기를 4배 증가시켜야 합니다.

표본 추출

• 보통은 모델을 만드는데 80% 정도의 데이터를 가지고 작업을 하고, 모델을 검증하는데 20% 정도의 데이터를 사용
• 해당 비중은 절대적인 것은 아니고, 7:3, 7:2:1(만들기7, 개선2, 검증1) 등의 경우도 존재한다.
• 데이터가 아주아주 많다면 5:5도 가능
• 데이터의 분포가일정하지 않다면, 가중치를 이용해서 데이터를 추출하는 것도 고려합니다.
• 아주 특별한 경우에는, 특정 조건을 만족하거나 특정 기간의 데이터만 이용하기도 합니다.

단순 임의 추출

• 데이터를 랜덤하게 추출
• 복원 추출
  - 추출된 데이터를 다시 집단에 넣어서 추출 - random.random 함수
• 비복원 추출
  - 추출된 데이터를 다시 집단에 넣지 않고 추출 - random.sample 함수
• random.range나 randint같은 함수도 제공

import random
#데이터 집단
li=[10,20,30,40,50]
# 복원 추출 - 같은 데이터가 나올 수 있다.
for i in li:
    print(li[random.randint(0,len(li)-1)])
# 비복원 추출 - li에서 복원하지 않고 k개 추출
# k>len(li) 면 터져버릴 것이다.
result=random.sample(li,k=3)
print(result)

• numpy에도 이러한 표본을 추출할 수 있는 함수를 제공함
• 확률은 층화 추출을 하기 위해서 사용
• choice(데이터배열, size=개수,replace=복원추출여부, p=확률)

ar=['바밤바','배뱀배','벼볌벼','비비빅','빙빙']
# numpy 복원 추출
print(np.random.choice(ar,4))
# 8:2 비복원 추출
# 일반적인 머신러닝에서 훈련데이터와 검증데이터 분리
sample=np.random.choice(ar,int(len(ar)*0.8),replace=False)
print(sample)
validation=[]
# 데이터를 순회하면서 속하지 않은 데이터만 validation에 추가
for i in ar:
    if i not in sample:
        validation.append(i)
print(validation)

분류 모델을 만드는 경우나, 회귀를 하는데 범주형 데이터가 존재하는데, 이 데이터들의 분포가 일정하지 않고, 이 범주형 데이터가 Target으로 사용되는 경우는 반드시 층화추출을 고민해야 합니다.
하지만, 이 데이터가 Target이 아니고 Feature라면, 모델을 여러 개 만드는 것 도 고민해봐야 합니다.

• 가중치를 줘보자.

# 가중치를 부여한 샘플 추출 - 층화 추출
# 분류 분석에서 이 속성이 Target으로 사용되는 경우에는
# 데이터의 개수를 파악한 후, 층화 추출 하는 것을 고려해보자.
print(np.random.choice(ar,3,p=[0.1,0.1,0.2,0.2,0.4]))

• 이를 층화추출이라고 합니다.

pandas 의 함수를 이용한 표본 추출

• Series와 DataFrame에서 sample이라는 함수를 이용합니다.

# help(pd.Series.sample)
# DataFrame에서의 샘플링
ex_df=pd.DataFrame(np.arange(0,120).reshape(40,3))
# print(ex_df)
# 행 단위로 꺼내주나봐
print(ex_df.sample(10))
# 단순히 10 하면 10개의 행을, n=10이면 데이터를 10개를
# 비율은 freq=0.8 이렇게 하면 된다.

머신 러닝에서 많이 사용하는 샘플링 방법

• scikit-learn 라이브러리의 model_select 클래스의 train_test_split 함수 이용
• 매개변수로 shuffle이나 층화추출을 위한 stratify 옵션도 제공

• 데이터 생성을 하고, 순차적 분할하기

X=np.arange(20).reshape(10,2)
y=np.arange(10)
# print(X)
# 순차적 분할 - 데이터를 순서대로 분할 : shuffle옵션 False
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test=train_test_split(X,y,
                                              test_size=0.3,
                                              shuffle=False,
                                              random_state=42)
print(X_train.shape)
print(X_test.shape)
print(y_train.shape)
print(y_test.shape)

• 무작위 추출을 해보자
• 표본 편향이란?
  - 모집단이 대표되도록 샘플을 추출해야 하는데, 유의미한 비임의 방식으로 표본이 추출되어서 발생하는 현상
  - 1936년 미국 대통령 선거에서 리터러리 다이제스트라는 곳의 예측과 갤럽의 에측이 상충되는 결과를 만들었는데, 리터러리 다이제스트는 1000만명이 넘는 샘플로, 갤럽은 200명으로 했는데 갤럽이 맞음
  - 리터러리 다이제스트는 자신들의 잡지 구독자를 대상으로 샘플링을, 갤럽은 랜덤 추출을 하였다.
  - 이 때, 리터러리 다이제스트는 사회 및 경제적 지위가 높은 사람들이 거의 대부분이었다.
• 자기 선택 표본 편향
  - 소셜 미디어 사이트에서 보는 가게 리뷰는 제출하는 사람들이 무작위로 선택되지 않았기에 편향되기 쉬움
  - 작성자 스스로 리뷰 작성에 대한 주도권을 갖기 때문인데, 이것이 자기 선택 편향이다.
  

# 랜덤 추출
# 랜덤 추출을 할 때, 이를 가지고 실제 훈련에 사용한다면
# 시드를 무조건 고정해야 한다.
# 선택된 데이터에 따라 다른 모델이 만들어지기 때문
# + 검증 데이터도 랜덤 생성이라 평가 지표가 매번 달라진다.
X_train,X_test,y_train,y_test=train_test_split(X,y,
                                              test_size=0.3,
                                              shuffle=True,
                                              random_state=42)
print(X_train.shape)
print(X_test.shape)
print(y_train.shape)
print(y_test.shape)

• 층화 무작위 추출

X=np.arange(30).reshape(15,2)
y=np.arange(15)
grep=[0,0,0,0,0,1,1,1,1,1,1,1,1,1,1]
# 층화 무작위 추출
X_train,X_test,y_train,y_test=train_test_split(X,y,
                                              test_size=0.3,
                                              shuffle=True,
                                              stratify=grep,
                                              random_state=42)
print(X_train.shape)
print(X_test.shape)
print(X_train)

재표본 추출

• 랜덤한 변동성을 알아보자는 일반적인 목표를 가지고 관찰된 데이터의 값에서 표본을 반복적으로 추출하는 것
• 일부 머신러닝 모델의 정확성을 평가하고 향상시키는데 적용
  - 여러 부트스트랩 데이터 집합을 기반으로 하는 각각의 의사 결정 트리 모델로 부터 나온 예측들로부터 배깅이라는 절차를 통해 평균 예측값을 구할 수 있습니다.

종류

• 순열 검정(Permutation test)
  - 두 개 이상의 표본을 함께 결합하여 관측값을 무작위로 재표본으로 추출하는 방식
• 부트스트랩(bootstrap)
  - 통계량이나 모델 매개변수의 표본 분포를 추정하기 위해서 현재 있는 표본에서 추가적으로 표본을 본원 추출하고 각 표본의 통계량과 모델을 다시 계산하는 과정

순열 검정

• 두 개 이상의 표본을 함께 결합해서 재표본으로 추출하는 과정
• 두 개 이상의 표본을 사용하며, 일반적으로 A/B 검정이나 가설검정을 위해 사용
• 과정
  - 여러 그룹의 결과를 하나읟 ㅔ이터 집합으로 합침
  - 결합된 데이터를 섞어 A 그룹과 동일한 크기의 표본을 무작위 추출
  - 나머지 데이터에서 B 그룹과 동일한 크기의 표본 무작위 추출
  - 여러 그룹들이 있다면, 동일한 작업 반복
  - 재추출된 표본을 가지고 다시 계산하고 기록을 합니다.
  - 이러한 과정을 R번 반복해서 검정 통계량의 순열 분포를 얻음
• 실험을 통해서 관찰한 그룹 간 차이와 순열 과정에서 얻은 집합에서의 차이를 비교
• 관찰한 차이가 순열로 보이는 차이의 집한 안에 있다면, 관찰한 차이가 우연히 보여진 것이고, 집합 안에 없다면 이것은 우연이 아니므로 통계적으로 유의미합니다.

부트스트랩

• 모수의 분포를 추정하는 방법으로 현재 있는 표본에서 추가적으로 표본을 복원추출하고 각 표본에 대한 통계량을 다시 계산하는 것
• 이 경우에, 데이터가 정규 분포를 따라야 한다는 가정이 필요하지 않음
• 개념적으로는 원래 표본을 여러 번 복제하는 것
• 1억개의 모집단에서 200개의 데이터를 표본으로 추출한 후 통계량을 구하는 것
  - 1. 200개의 표본 중 1개의 데이터를 뽑아서 기록하고 다시 복구시킴
  - 2. 이 작업을 N번 반복함
  - 3. N번 추출한 데이터를 가지고 평균을 구함
  - 4. 이 과정을 R번 반복(R은 부트스트랩 횟수)
  - 5. R개의 평균에 대한 결과를 사용해서 신뢰구간을 구함
  - R의 크기가 커질수록 신뢰 구간에 대한 추정이 더 정확
• coffee_dataset.csv 파일
  - 21살 미만 여부, 커피 마시는지, 키
• 위의 데이터를 이용해서 알고자 하는 사실
  - 커피를 마시는 사람과 안마시는 사람의 평균 키 차이
  - 21살 이상과 21살 미만의 평균 키 차이
  - 21살 미만인 경우 커피 여부에 따른 키 차이
  - 21살 이상인 경우 커피 여부에 따른 키 차이 등...
  

# 커피를 마시는 사람과 안마시는 사람의 키 평균 차이
# 반복 횟수
iterationNum=10000
diffHeightList=[]
for _ in range(iterationNum):
    bootSample=df_sample.sample(200,replace=True) #복원 추출
    # 커피 안마시는 사람 평균 키
    nonCoffeeHeightMean=bootSample[bootSample['drinks_coffee']==False].height.mean()
    # 커피를 마시는 사람 평균 키
    coffeeHeightMean=bootSample[bootSample['drinks_coffee']==True].height.mean()
    # 차이 구하기
    diff=nonCoffeeHeightMean-coffeeHeightMean
    # 리스트 추가
    diffHeightList.append(diff)
print(len(diffHeightList))

# 신뢰 구간 99.5% 인 평균 키 차이에 대한 신뢰구간
print(np.percentile(diffHeightList,0.5),np.percentile(diffHeightList,99.5))

# 21세 이상과 21세 미만의 키 평균 차이를 구해보자.
iterationNum=10000
diffHeightList=[]
for _ in range(iterationNum):
    bootSample=df_sample.sample(200,replace=True) #복원 추출
    # 21세 이상인 사람 평균 키
    over21HeightMean=bootSample[bootSample['age']=='>=21'].height.mean()
    # 21세 미만인 사람 평균 키
    under21HeightMean=bootSample[bootSample['age']=='<21'].height.mean()
    # 차이 구하기
    diff=over21HeightMean-under21HeightMean
    # 리스트 추가
    diffHeightList.append(diff)

print(len(diffHeightList))
# 신뢰 구간 99.5% 인 평균 키 차이에 대한 신뢰구간
print(np.percentile(diffHeightList,0.5),np.percentile(diffHeightList,99.5))

✔ 추론 통계

추론 통계 - 통계적 추록

• 기술 통계
  - 주어진 데이터의 분포나 빈도, 평균 등의 통계량을 통해서 데이터를 설명하는 것이 목적
• 추록 통계
  - 주어진 데이터를 이용해서 모집단의 특성을 추론하는 것이 목적
• 제한된 데이터로 주어진 실험 결과를 더 큰 과정 또는 모집단에 적용하려는 의도를 반영하는 것을 추론(Inference)
• 가설 검정을
• 추론 과정
  - 가설 세움
  - 실험 설계
  - 데이터 수집
  - 추론 및 결론 도출
  

확률 분포의 추정

• 분석할 데이터는 어떤 확률 변수로부터 실현된 표본이다 라는 데이터 분석의 첫 번째 가정

확률 분포의 결정

• 확률 변수가 베르누이 분포, 이항 분포, 정규 분포 등의 기본 분표

시각화를 이용해서 히느를 얻어서 결정

• 데이터가 0 또는 1 : 베르누이 분포
• 데이터가 카테고리 : 카테고리 분포
• 데이터가 0에서 1사이 : 베타 분포
• 데이터가 0과 양수
  - 로그 정규, 감마, F, 카이제곱, 지수, 하프코시 분포 등..
• 데이터의 크기가 제한이 없는 경우
  - 정규, 스튜턴트 t, 코시, 라플라스 분포 등...

모수 추정 방법론을 이용한 확률 분포의 결정

• 모수 추정은 모수의 값으로 가장 가능성이 높은 하나의 숫자를 찾아내는 작업이 모수 추정이다.
• 모수 추정 방법
  - 모멘트 방법
  - 최대 가능도 추정법
  - 베이즈 추정법
• 모멘트 방법
  - 평균, 분산, 왜도, 첨도
• 최대 가능도 추정법
  - 확률 질량 함수나 누적 밀도 함수를 이용해서 추정
• 베이즈 추정법
  - 모수 값이 가질 수 있는 모든 가능성의 분포를 계산하는 작업

추정

검정(testing)

• 데이터 뒤에 숨어있는 확률 변수의 분포와 모수에 대한 가설의 진위를 정량적으로 증명하는 작업
• 작업
  - 어떤 동전을 15번 던졌더니 앞면이 12번 나왔는데, 이 동전은 조작되지 않은 공정한 동전인가?
  - 어떤 주식의 수익률이 -2.5%, -5%, 4.3%, -3.7%, -5.6%인 경우, 이 주식은 장기적으로 수익을 가져다 줄 수 있는가?
  

통계적 추정

• 점 추정
  - 모집단의 특성을 하나의 값으로 추정
• 구간 추정
  - 모집단의 특성을 적절한 구간을 이용하여 추정하는 방식
  - 신뢰수준 : 계산된 구간이 모수를 포함할 확률을 의미, 90, 95, 99% 사용
  - 신뢰구간 : 신뢰 수준 하에서 모수를 포함하는 구간으로, 상한과 하한으로 표현
  - 표본오차 : 모집단에서 추출한 표본이 모집단 특성과 정확히 일치하지 않아서 발생하는 확률의 차이

---

• 대통령 후보의 지지율 여론조사에서 후보의 지지율이 95% 신뢰수준에서 표본 오차 +-3% 범위에서 32.4% 로 조사된 경우
  - 실제 지지율은 29.4% ~ 35.4% 사이에 나타날 가능성이 95% 이고, 그러지 않을 가능성이 5%이다.

---

가설

• 데이터를 특정한 확률 분포를 가진 확률 변수로 모형화를 하면, 모수를 추정할 수 있는데, 모술를 추정한 후 데이터 뒤에 숨어있는 확률 변수가 정말로 그 모수 값을 가졌는지 검증을 해야 하는데, 이때 이 확률 분포에 대한 어떤 주장을 가설이라고 합니다.

• 귀무가설
  - 해당 규칙에 따라 표본 데이터 집합에서 어떤 숫자를 계산하면, 계산된 숫자는 특정한 확률 분포를 따르게 되는데, 이 숫자를 검정 통계치라고 하며 이 때의 확률 분포를 검정 확률 분포라 하며 검점 통계 분포의 종류 및 모수의 값은 처음에 정한 가설에 의해 결정되며, 이렇게 검정 통계 분포를 결정하는 최초의 가설
  - 우연에 의해 발생한 것이라는 개념을 구체화하기 위해서 사용하는 논리적 구조

• 대립가설
  - 귀무가설의 반대

• 귀무가설 : A와 B의 평균에는 차이가 없다 / 대립가설 : A와 B의 평균에는 차이가 있다.

일원검정과 이원검정

• 일원검정
  - 한 방향으로만 검정하는 것
  - 크다 작다 등..
• 이원검정
  - 양 방향으로 검정하는 것
  - 상한과 하한
• R이나 Python의 검정 method들은 기본적으로 이원검정(조금 더 보수적이다.)

통계적 유의성

• 실험 결과가 우연히 일어난 것인지, 아니면 우연이 아닌지 판단하는 방법
• 결과가 우연히 벌어질 수 있는 변동성의 바깥에 존재하면, 이것을 통계적으로 유의하다라고 합니다.
• 용어
  - p-value : 귀무가설을 구체화한 기회 모델이 주어졌을 때, 관측된 결과와 같이 특이하거나 극단적인 결과를 얻을 확률로 유의확률이라고 합니다. 이 값은 대부분 모델이 생성해줍니다.
  - alpha : 실제 결과가 토계적으로 의미있는 것으로 간주되기 위해, 우연에 의한 결과가 능가해야 하는 비정상적인 가능성의 임계 확률. 이 값은 분석가나 개발자가 임의로 설정합니다.
  - 제 1종 오류 : 우연에 의한 효과를 실제 효과라고 잘못 결론 내리는 것
  - 제 2종 오류 : 실제 효과를 우연에 의한 효과라고 잘못 결론 내리는 것

---

웹 테스트의 결과에 의한 통계적 유의성
가격 A : 전환 200, 비전환, 23,539
가격 B : 전활 182, 비전환, 22,406

• 가격 A의 전환율 : 0.8425%
• 가격 B의 전환율 : 0.8075%
• A-B : 0.0350% 의 전환율 개선 - 의미가 있는지 여부?

통계적 유의성 검사

• 전체 데이터와 전환된 데이터를 구분해서 저장하기
  - 전환되지 않은 데이터 : 45,945
  - 전환 데이터 : 382
• 가격 A인 경우 23,739개의 샘플을 뽑아서 1이 몇 개 인지 확인
• 가격 B인 경우 22,406개의 샘플을 뽑아서 1이 몇 개 인지 확인
• 1의 비율 차이를 기록하고, 이 작업을 반복한 후, 이 차이가 얼마나 자주 >=0.0350인지 확인
• 횟수를 직접 보는 것 보다는 p-value를 계산해서 유의미한 결과인지 확인
  - α 값을 설정해서, α값이 p-value보다 크다면 이 경우는 우연히 이런 결과가 나온 것이라고 할 수 있고, α값이 p-value 보다 작다면 이 경우는 우연히 이러한 결과가 나온 것이 아니다 라고 할 수 있습니다.
  - α(유의수준)값이 p-value 보다 작다면, 이 경우는 가격을 변경한 것이 효과가 있었다 라고 할 수 있습니다.

• 웹 테스트의 경우 도움말 : https://marketingplatform.google.com/intl/ko/about/optimize/
  - google analytics에서 데이터 제공하니 이걸로 해보자.