이진 트리 순회

• 이진 트리가 순환적으로 정의되어 구성되어있으므로, 순회 작업도 서브 트리에 대해서 순환적으로 반복하여 완성한다.

• 왼쪽 서브 트리에 대한 순회를 오른쪽 서브 트리보다 먼저 수행한다.

• 순회의 종류

  • 전위 순회

  • 중위 순회

  • 후위 순회

• 전위 순회 (preorder traversal)

  • D → L → R 순서로, 현재 노드를 방문하여 처리하는 작업 D를 가장 먼저 수행

    

  • 전위 순회 예)

    

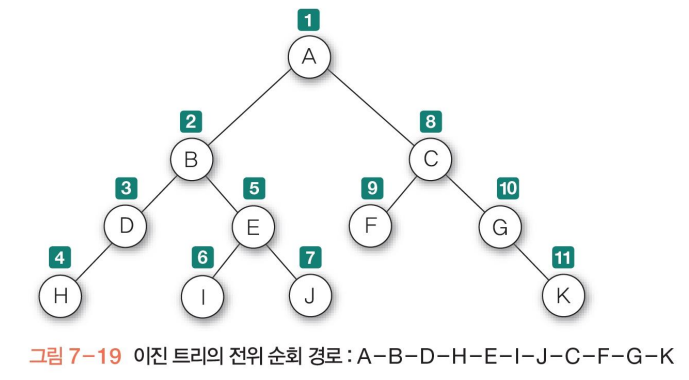
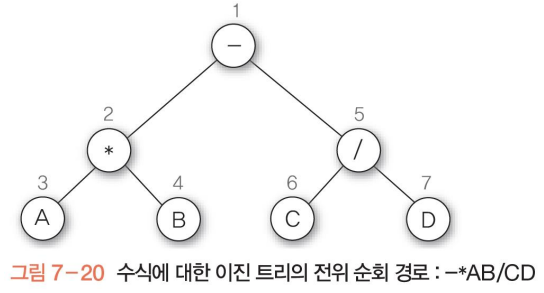
  • 수식 A * B - C / D를 이진 트리로 구성

    • 수식에 대한 이진 트리를 전위 순회하면, 전위 표기식을 구할 수 있음

      

• 중위 순회 (inorder traversal)

  • L → D → R 순서로, 현재 노드를 방문하는 작업 D를 작업 L과 작업 R의 중간에 수행

    

  • 중위 순회 예)

    

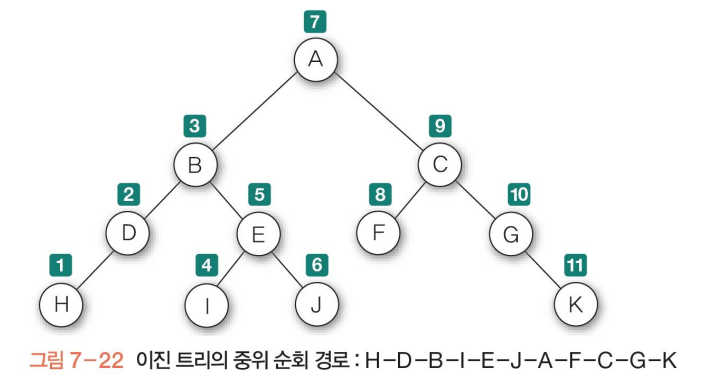
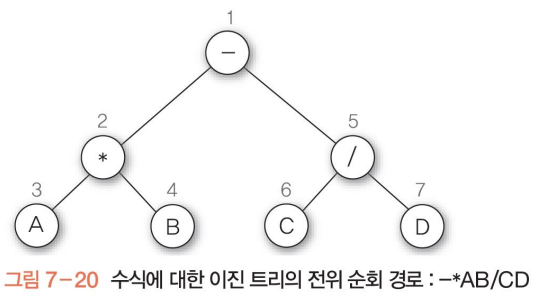
  • 수식 A * B - C / D를 이진 트리로 구성

    • 수식 이진 트리를 중위 순회하면, 수식에 대한 중위 표기식을 구할 수 있음

      

• 후위 순회

  • L-R-D 순서로 현재 노드를 방문하는 D 작업을 가장 나중에 수행

    

  • 후위 순회 예)

    

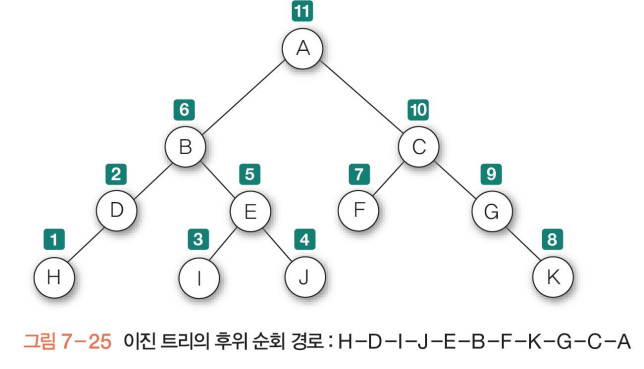
  • 수식 A * B - C / D를 이진 트리로 구성

    • 수식 이진 트리를 후위 순회하면, 수식에 대한 후위 표기식을 구할 수 있음

      

이진 트리 순회 코드

void preorder(Node root) {
	if (isTreeEmpty(root)) {
		return;
	}
	else {
		printf("%c ", getCurData(root));
		preorder(getLeftChild(root));
		preorder(getRightChild(root));
	}
}

void inorder(Node root) {
	if (isTreeEmpty(root)) {
		return;
	}
	else {
		inorder(getLeftChild(root));
		printf("%c ", getCurData(root));
		inorder(getRightChild(root));
	}
}

void postorder(Node root) {
	if (isTreeEmpty(root)) {
		return;
	}
	else {
		postorder(getLeftChild(root));
		postorder(getRightChild(root));
		printf("%c ", getCurData(root));
	}
}

void main() {
	Node a = makeRoot('A');
	Node b = makeLeftChild(a, 'B');
	Node c = makeRightChild(a, 'C');
	Node d = makeLeftChild(b, 'D');
	Node e = makeRightChild(b, 'E');
	Node f = makeLeftChild(c, 'F');
	Node g = makeRightChild(c, 'G');

	printf("전위순회: ");  preorder(a); printf("\n");
	printf("중위순회: ");  inorder(a); printf("\n");
	printf("후위순회: ");  postorder(a); printf("\n");
}

-> 실행결과