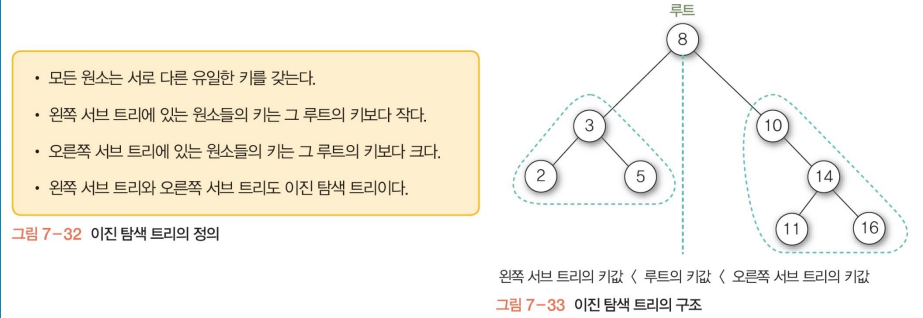
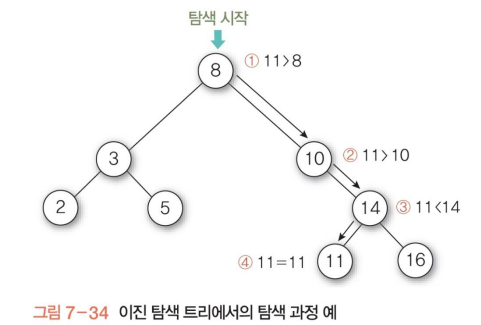
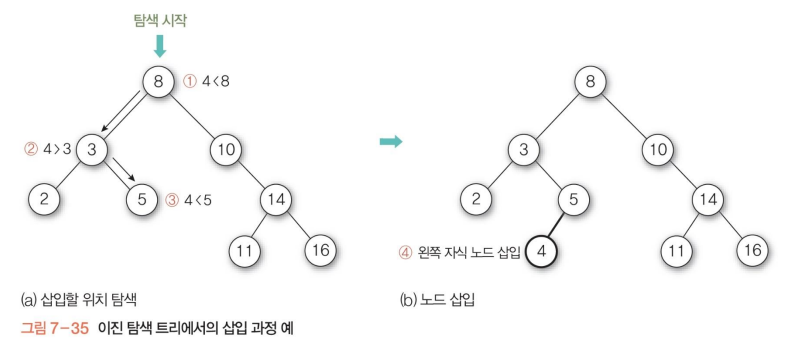
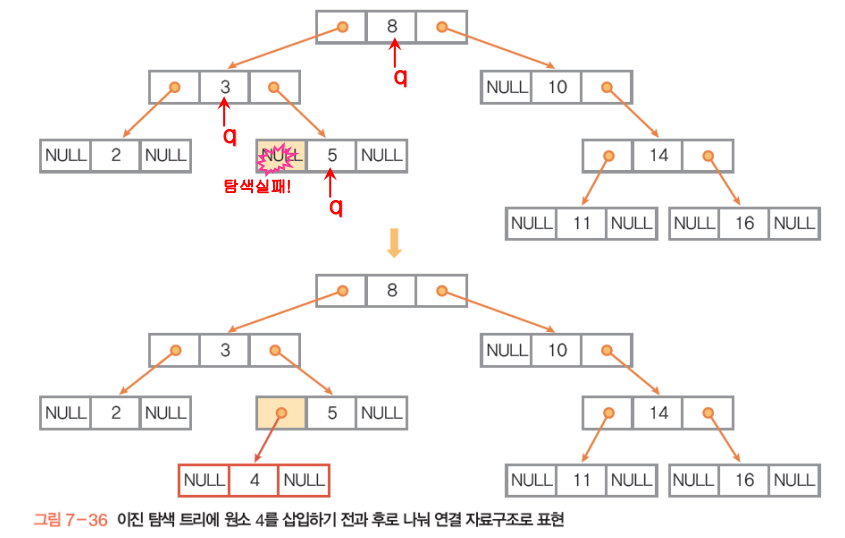
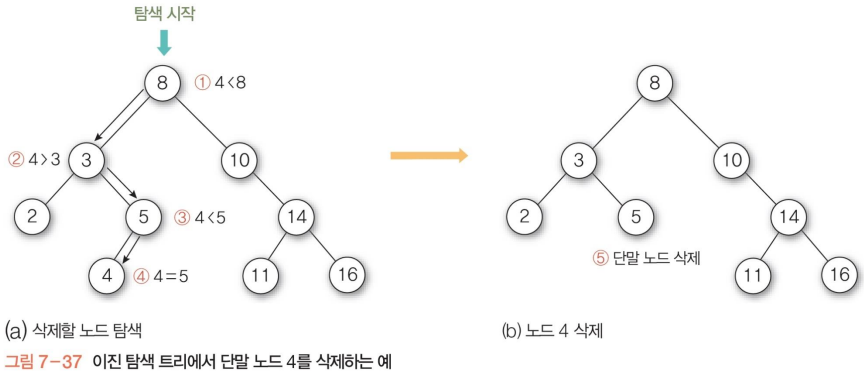
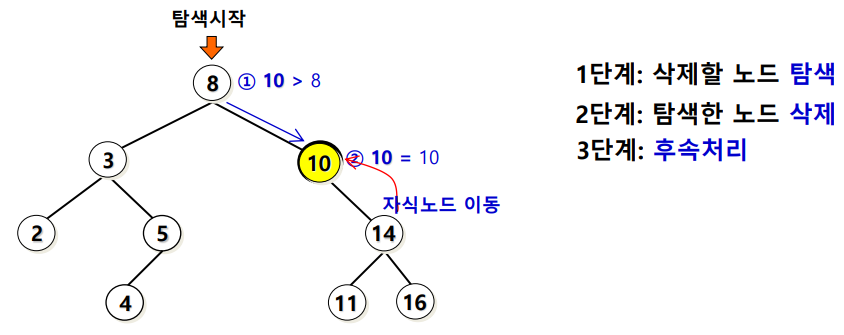
이진 탐색 트리 (BST, Binary Search Tree)
이진 탐색 트리
이진 트리를 탐색용 자료구조로 사용하기 위해 원소 크기에 따라 노드 위치를 정의한 것
이진 탐색 트리 조건
모든 원소는 유일한 키 값을 갖는다.
왼쪽 서브트리의 모든 원소들은 루트의 키보다 작은 값을 갖는다.
오른쪽 서브트리의 모든 원소들은 루트의 키보다 큰 값을 갖는다.
왼쪽 서브트리와 오른쪽 서브트리도 이진탐색트리이다.
이진 탐색 트리에서 원소 11을 탐색
1. (찾는 키값 11＞루트 노드의 키값 8)이므로 오른쪽 서브 트리 탐색
2. (찾는 키값 11＞노드의 키값 10)이므로 다시 오른쪽 서브 트리 탐색
3. (찾는 키값 11＜노드의 키값 14)이므로 왼쪽 서브 트리 탐색
4. (찾는 키값 11 = 노드의 키값 11)이므로 탐색 성공으로 연산 종료
이진 탐색 트리의 삽입 연산
1. 먼저 탐색 연산을 수행
삽입할 원소와 같은 원소가 트리에 있으면 삽입할 수 없으므로, 같은 원소가 트리에 있는지 탐색하여 확인
탐색에서 탐색 실패가 결정되는 위치가 삽입 위치가 됨
2. 탐색 실패한 위치에 원소를 삽입
이진 탐색 트리에 원소 4를 삽입하기
1. (찾는 키값 4＜루트 노드의 키값 8)이므로 왼쪽 서브 트리를 탐색
2. (찾는 키값 4＞노드의 키값 3)이므로 오른쪽 서브 트리를 탐색
3. (찾는 키값 4＜노드의 키값 5)이므로 왼쪽 서브 트리를 탐색해야 하지만, 왼쪽 자식 노드가 없으므로 노드 5의 왼쪽 자식 노드에서 탐색 실패가 발생
4. 실패가 발생한 자리, 즉 노드 5의 왼쪽 자식 노드 자리에 노드 4를 삽입
이진 탐색 트리에 원소 4를 삽입하는 과정을 연결 자료구조로 표현
이진 탐색 트리의 삭제 연산
먼저 탐색 연산을 수행
삭제할 노드의 위치를 알아야 하므로 트리를 탐색
탐색하여 찾은 노드를 삭제
노드의 삭제 후에도 이진 탐색 트리를 유지해야 하므로 삭제 노드의 경우에 대한 후속 처리(이진 탐색 트리의 재구성 작업)가 필요함
- 삭제할 노드의 경우
삭제할 노드가 단말 노드인 경우 (차수 = 0)
삭제할 노드가 자식 노드를 한 개 가진 경우 (차수 = 1)
삭제할 노드가 자식 노드를 두 개 가진 경우 (차수 = 2)
삭제할 노드가 단말 노드인 경우(차수 = 0)의 삭제 연산
노드 4를 삭제하는 경우
삭제할 노드가 자식 노드를 한 개 가진 경우(차수 = 1)의 삭제 연산
노드를 삭제하면 자식 노드는 트리에서 연결이 끊어져서 고아가 됨
후속처리: 삭제한 부모 노드의 자리를 자식 노드에게 물려줌
노드 10을 삭제하는 경우
삭제할 노드가 자식 노드를 두 개 가진 경우(차수 = 2)의 삭제 연산
노드를 삭제하면, 자식 노드들은 트리에서 연결이 끊어져서 고아가 됨
후속 처리 : 삭제한 노드의 자리를 자손 노드들 중에서 선택한 후계자에게 물려줌
후계자 선택 방법
왼쪽 서브 트리에서 가장 큰 자손 노드 선택 :
왼쪽 서브 트리의 오른쪽 링크를 따라 계속 이동하여 오른쪽 링크 필드가 NULL인 노드 즉, 가장 오른쪽 노드가 후계자가 됨
오른쪽 서브 트리에서 가장 작은 자손 노드 선택 :
오른쪽 서브 트리에서 왼쪽 링크를 따라 계속 이동하여 왼쪽 링크 필드가 NULL인 노드 즉, 가장 왼쪽에 있는 노드가 후계자가 됨
이진 탐색 트리 코드
#include <stdio.h>
#include <stdlib.h>
typedef char data;
typedef struct _Node {
char key;
struct _Node* left;
struct _Node* right;
}Node;
Node* searchBST(Node* root, char x) {
Node* p = NULL;
p = root;
while (p != NULL) {
if (p->key == x) {
return p;
}
else if (p->key < x) {
p = p->right;
}
else {
p = p->left;
}
}
printf("찾는 키가 존재하지 않습니다.\n");
return NULL;
}
Node* insertBST(Node* root, char x) {
Node* p = root;
Node* parent = NULL;
while (p != NULL) {
parent = p;
if (p->key == x) {
printf("같은 키가 존재합니다.\n");
return p;
}
else if (p->key < x) {
p = p->right;
}
else {
p = p->left;
}
}
// 새 노드 할당
Node* newNode = (Node*)malloc(sizeof(Node));
newNode->key = x;
newNode->left = NULL;
newNode->right = NULL;
// parent의 자식으로 새 노드 붙이기
if (parent != NULL) {
if (parent->key < newNode->key) {
parent->right = newNode;
}
else {
parent->left = newNode;
}
}
return newNode;
}
Node* deleteBST(Node* root, char x) {
Node* p = root;
Node* parent = NULL;
while ((p != NULL) && (p->key != x)) {
parent = p;
if (p->key < x) {
p = p->right;
}
else {
p = p->left;
}
}
if (p == NULL) {
printf("찾는 노드가 존재하지 않습니다.\n");
return root;
}
// 차수가 0인 경우
if (p->left == NULL && p->right == NULL) {
if (parent != NULL) {
if (parent->left == p) {
parent->left = NULL;
}
else {
parent->right = NULL;
}
}
else root = NULL;
}
// 차수가 1인 경우
else if (p->left == NULL || p->right == NULL) {
Node* child = NULL;
if (p->left != NULL) {
child = p->left;
}
else {
child = p->right;
}
if (parent != NULL) {
if (parent->left == p) {
parent->left = child;
}
else {
parent->right = child;
}
}
else root = child;
}
// 차수가 2인 경우
else {
Node* succ_parent = p;
Node* succ = p->right;
while (succ->left != NULL) { // 오른쪽 서브 트리에서 후계자 찾기
succ_parent = succ;
succ = succ->left;
}
if (succ_parent->left == succ) {
succ_parent->left = succ->right;
}
else {
succ_parent->right = succ->right;
}
p->key = succ->key;
p = succ;
}
free(p);
}
void inorder(Node* root) {
if (root == NULL) {
return;
}
else {
inorder(root->left);
printf("%c ", root->key);
inorder(root->right);
}
}
int main() {
Node* root = insertBST(NULL, 'D');
insertBST(root, 'I');
insertBST(root, 'F');
insertBST(root, 'A');
insertBST(root, 'G');
insertBST(root, 'C');
inorder(root); printf("\n");
deleteBST(root, 'C');
inorder(root); printf("\n");
return 0;
}
Beginner_Developer