트리
원소들 간에 1:n 관계를 가지는 비선형 자료구조
원소들 간에 계층관계를 가지는 계층형 자료구조
상위 원소에서 하위 원소로 내려가면서 확장되는 트리(나무)모양의 구조
트리의 구성요소
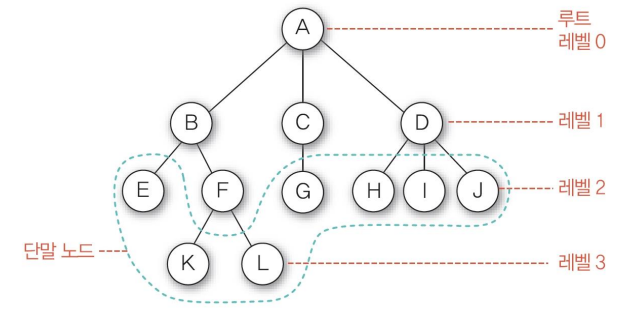
노드node – 트리의 원소
트리 A의 노드 - A,B,C,D,E,F,G,H,I,J,K,L
루트 노드root node – 트리의 시작 노드(레벨Level 0)
간선edge – 노드를 연결하는 선. 부모Parent 노드와 자식Child 노드를 연결
형제 노드sibling node – 같은 부모 노드의 자식 노드들
조상 노드Ancestor – 간선을 따라 루트 노드까지 경로에 있는 모든 노드들
서브 트리subtree – 부노 노드와 연결된 간선을 끊었을 때 생성되는 트리
각 노드는 자식 노드의 개수 만큼 서브 트리를 가짐
자손 노드 – 서브 트리에 있는 하위 레벨의 노드들
차수degree
노드의 차수 : 노드에 연결된 자식 노드의 수.
A의 차수=3, B의 차수=2, C의 차수=1
트리의 차수 : 트리에 있는 노드의 차수 중에서 가장 큰 값
단말 노드(리프 노드) : 차수가 0인 노드. 자식 노드가 없는 노드
높이
노드의 높이 : 루트에서 노드에 이르는 간선의 수. 노드의 레벨
트리의 높이 : 트리에 있는 노드의 높이 중에서 가장 큰 값. 최대 레벨
포리스트forest : 서브 트리의 집합
트리 A에서 노드 A를 제거하면, A의 자식 노드 B, C, D에 대한 서브 트리가 생기고, 이들의 집합은 포리스트가 됨
이진 트리 (Binary Tree)
트리의 모든 노드의 차수를 2 이하로 제한하여 전체 트리의 차수가 2이하가 되도록 정의
이진 트리의 모든 노드는 왼쪽 자식 노드와 오른쪽 자식 노드만 가짐
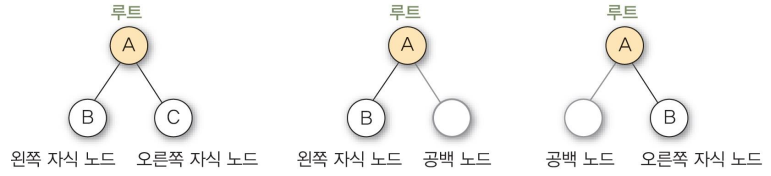
일반 트리를 이진 트리로 변환

이진 트리의 특성
노드가 n개인 이진 트리는 항상 간선이 (n-1)개임
루트를 제외한 (n-1)개의 노드가 부모 노드와 연결되는 한 개의 간선을 가짐
높이가 h인 이진 트리가 가질 수 있는 노드 개수는 최소 (h+1)개이며, 최대(2^(h+1)-1)개
이진 트리의 높이가 h가 되려면 한 레벨에 최소한 한 개의 노드가 있어야 하므로 높이가 h인 이진 트리의 최소 노드의 개수는 (h+1)개
하나의 노드는 최대 2개의 자식 노드를 가질 수 있으므로 레벨 i에서의 노드의 최대 개수는 2^i개 이므로 높이가 h인 이진 트리 전체의 노드 개수는 2^(h+1)-1 개
이진 트리의 종류
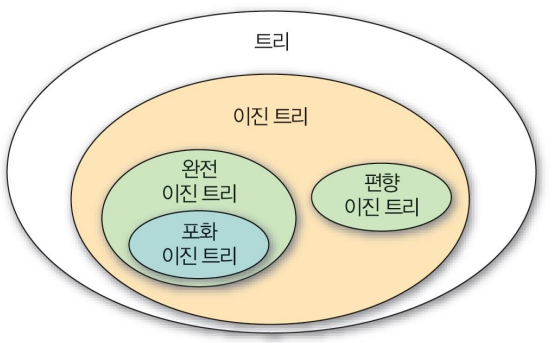
포화 이진 트리 (Full Binary Tree)
모든 레벨에 노드가 포화상태로 차 있는 이진 트리
높이가 h일 때, 최대의 노드 개수인 (2^(h+1)-1)의 노드를 가진 이진 트리
루트를 1번으로 하여 2^(h+1)-1까지 정해진 위치에 대한 노드 번호를 가짐
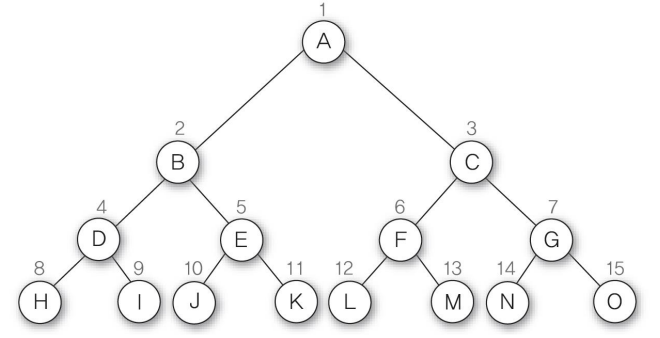
완전 이진 트리 (Complete Binary Tree)
높이가 h이고 노드 수가 n개일 때 (단, n < 2^(h+1)-1 ), 노드 위치가 포화 이진 트리에서의 노드 1번부터 n번까지의 위치와 완전히 일치하는 이진 트리
완전 이진 트리에서는 (n+1)번부터 (2^(h+1)-1 )번까지 노드는 모두 공백 노드
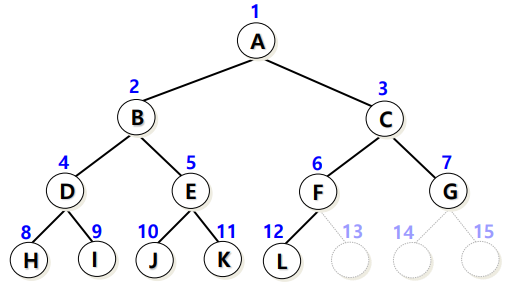
편향 이진 트리 (Skewed Binary Tree)
높이가 h일 때 h+1개의 노드를 가지면서 모든 노드가 왼쪽이나 오른쪽 중 한 방향으로만 서브 트리를 가지고 있는 트리
이진 트리 구현
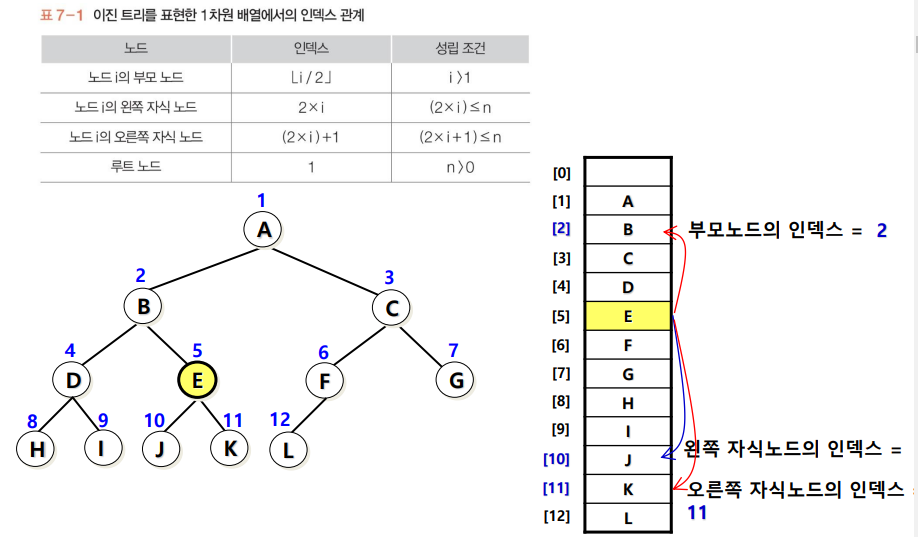
배열 구현
1차원 배열의 순차 자료구조 사용
높이가 h인 포화 이진 트리의 노드번호를 배열의 인덱스로 사용
인덱스 0번 : 실제로 사용하지 않고 비워둠.
인덱스 1번 : 루트 저장
완전 이진 트리의 1차원 배열 표현
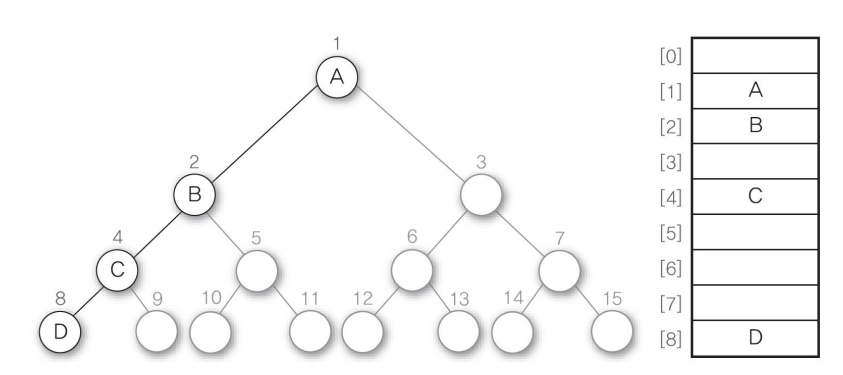
편향 이진 트리의 1차원 배열 표현
장점
완전 이진트리 같은 경우에 적합
노드 접근이 빠름
구현하기가 쉬움
단점
편향 이진트리 같은 경우, 많은 공간(메모리)이 낭비됨
배열 크기 이상의 노드를 추가할 수 없음
연결리스트 구현
연결 자료구조를 이용한 이진트리의 구현
포인터를 사용하여 이진트리 구현
데이터를 저장하는 데이터 필드, 왼쪽 자식 노드를 연결하는 왼쪽 링크 필드, 오른쪽 자식 노드를 연결하는 오른쪽 링크 필드로 구성. 자식 노드가 없으면 링크 필드에 NULL을 저장하여 NULL 포인터로 설정
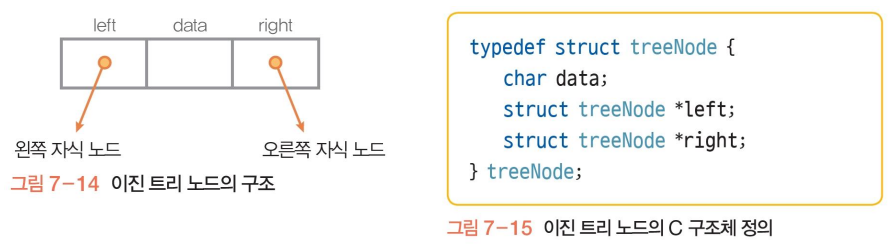
완전 이진 트리에 대한 연결 자료구조 표현
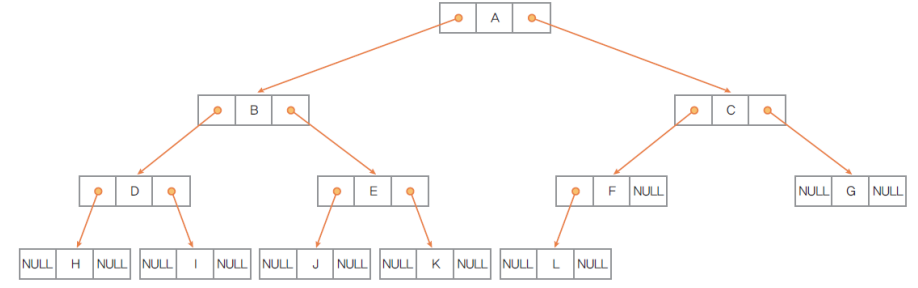
편향 이진 트리에 대한 연결 자료구조 표현
장점
삽입, 삭제가 쉬움
포인터로 연결하기 때문에 노드 수에 제한이 없음
메모리낭비가 없음
단점
배열보다 접근 속도가 느림
부가적인 메모리 필요
이진트리 배열 코드
BinaryTreeArray.h
#ifndef _BINARYTREE_H
#define _BINARYTREE_H
#include <stdio.h>
#include <stdlib.h>
#include <memory.h>
// 노드의 데이터 타입
typedef char DATA;
// 노드: tree[]의 index로써 노드를 가리킴.
typedef int Node;
Node makeRoot(DATA data);
Node makeLeftChild(Node cur, DATA data);
Node makeRightChild(Node cur, DATA data);
DATA getCurData(Node cur);
Node getLeftChild(Node cur);
DATA getLeftChildData(Node cur);
Node getRightChild(Node cur);
DATA getRightChildData(Node cur);
int isTreeEmpty(Node root);
#endif // _BINARYTREE_H
BinaryTreeArray.c
#include "BinaryTreeArray.h"
// 트리
#define NODE_MAXCOUNT 100
DATA tree[NODE_MAXCOUNT] = { 0 }; // 0값을 empty로 표시함.
// 배열크기가 넘어가면 에러가 나서 예외처리를 해야하지만 이 코드는 하지 않음.
Node makeRoot(DATA data) {
tree[1] = data;
return 1;
}
Node makeLeftChild(Node cur, DATA data) {
tree[cur * 2] = data;
return cur * 2;
}
Node makeRightChild(Node cur, DATA data) {
tree[cur * 2 + 1] = data;
return cur * 2 + 1;
}
DATA getCurData(Node cur) {
return tree[cur];
}
Node getLeftChild(Node cur) {
return cur * 2;
}
DATA getLeftChildData(Node cur) {
return tree[cur * 2];
}
Node getRightChild(Node cur) {
return cur * 2 + 1;
}
DATA getRightChildData(Node cur) {
return tree[cur * 2 + 1];
}
int isTreeEmpty(Node root) {
if (tree[root] == 0) {
return 1;
}
else {
return 0;
}
}
main.c
#include "BinaryTreeArray.h"
void main() {
Node n1 = makeRoot('-');
Node n2 = makeLeftChild(n1, '*');
Node n3 = makeRightChild(n1, '/');
Node n4 = makeLeftChild(n2, 'A');
Node n5 = makeRightChild(n2, 'B');
Node n6 = makeLeftChild(n3, 'C');
Node n7 = makeRightChild(n3, 'D');
char Data = getCurData(1);
printf("%c", Data);
Data = getCurData(2);
printf("%c", Data);
Data = getCurData(3);
printf("%c", Data);
Data = getCurData(4);
printf("%c", Data);
Data = getCurData(5);
printf("%c", Data);
Data = getCurData(6);
printf("%c", Data);
Data = getCurData(7);
printf("%c", Data);
}
이진 트리 연결리스트 코드 (순회 포함)
traversalBT.h
#pragma once
typedef char element;
typedef struct treeNode { // 연결 자료구조로 구성하기 위해 트리의 노드 정의
element data;
struct treeNode* left; // 왼쪽 서브 트리에 대한 링크 필드
struct treeNode* right; // 오른쪽 서브 트리에 대한 링크 필드
} treeNode;
treeNode* makeRootNode(element data, treeNode* leftNode, treeNode* rightNode);
void preorder(treeNode* root);
void inorder(treeNode* root);
void postorder(treeNode* root);
traversalBT.c
#include <stdio.h>
#include <stdlib.h>
#include "traversalBT.h"
// data를 루트 노드로 하여 왼쪽 서브 트리와 오른쪽 서브 트리를 연결하는 연산
treeNode* makeRootNode(element data, treeNode* leftNode, treeNode* rightNode) {
treeNode* root = (treeNode*)malloc(sizeof(treeNode));
root->data = data;
root->left = leftNode;
root->right = rightNode;
return root;
}
// 이진 트리에 대한 전위 순회 연산
void preorder(treeNode* root) {
if (root != NULL) {
printf("%c", root->data);
preorder(root->left);
preorder(root->right);
}
}
// 이진 트리에 대한 중위 순회 연산
void inorder(treeNode* root) {
if (root != NULL) {
inorder(root->left);
printf("%c", root->data);
inorder(root->right);
}
}
// 이진 트리에 대한 후위 순회 연산
void postorder(treeNode* root) {
if (root != NULL) {
postorder(root->left);
postorder(root->right);
printf("%c", root->data);
}
}
main.c
#include <stdio.h>
#include "traversalBT.h"
int main(void) {
// (A*B-C/D) 수식 이진 트리 만들기
treeNode* n7 = makeRootNode('D', NULL, NULL);
treeNode* n6 = makeRootNode('C', NULL, NULL);
treeNode* n5 = makeRootNode('B', NULL, NULL);
treeNode* n4 = makeRootNode('A', NULL, NULL);
treeNode* n3 = makeRootNode('/', n6, n7);
treeNode* n2 = makeRootNode('*', n4, n5);
treeNode* n1 = makeRootNode('-', n2, n3);
printf("\n preorder : ");
preorder(n1);
printf("\n inorder : ");
inorder(n1);
printf("\n postorder : ");
postorder(n1);
//getchar();
return 0;
}
이진 트리 역할
수식트리(Expression Tree)
허프만 코딩 트리(Huffman coding tree)
이진 검색 트리(Binary Search Tree, BST)
우선 순위 큐(PQ)













