Lab05) SVM
#복습을 위한 수업내용 리뷰이므로 글이 정리되어 있지 않습니다.
인공지능 프로그래밍 (230920)
lr복습) cost함수는 output과 다름.
(아래에서 언급되는 NN은 neural network를 의미합니다.)
SVM(NN과 다름) 딥러닝 아닌 머신러닝.
NN의 층을 쌓기 시작하다 보면 계산량이 너무 늘어나서 잘 안되기 시작, 이를 보완하기 위해서 고안된 것이 support vector machine!
non-linear할때도 잘 동작한다.

(위키백과: 서포트벡터머신 그림 참조)
즉, 잘 만든 nn과 같은데 굳이 쓰는 이유는 계산량을 많이 줄일 수 있기 때문.
Kernel method 는 probability density estimation. 특정함수를 거쳐서 거기서 나온값을 통해 원래 알고리즘을 동작시키는 것->kernel.
데이터셋이 충분히 큰 상황에서도 충분히 좋은 결과를 낸다.
빠르고 좋은성능-> 같이 달성했다는게 svm의 특징
Full bayesian framework=NN->computationally expensive.
gpgpu의 도래->계산량 극복가능 시점 부터 딥러닝이 주로 쓰이게 되었음.
과적합(overfitting)을 막으면서도 잘 동작하게함.
dataset이 잘 구비가 안되면 NN잘 구동이 안된다.
편중되거나 과적합되는 경우가 발생
이러한 경우에 대해서 좀 더 자유로운 형태가 바로
->SVM
이것이 가능한 이유는 전체 데이터셋을 사용하지 않기 때문.
데이터가 많은 쪽으로 기울어질 수 밖에 없음.
NN은 데이터가 중요하다.
데이터의 퀄리티 중요.->데이터에 대한 estimatation이 되기 때문에(평균이라던가)
문제가 된다.
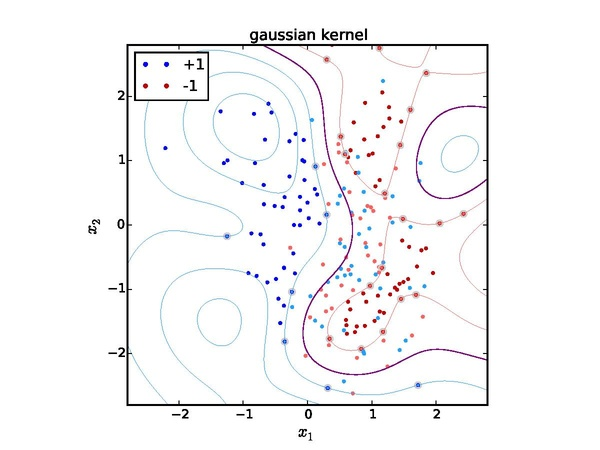
SVM은 중간에 선을 그어서 그 선이 classification이 되는 데이터에 가장 가운데가 되도록 = maximum margin이 되도록
결국 가운데 선이 두 class와 최대 거리가 되도록!
NN은 데이터가 많으면 그쪽으로 움직이는 반면!
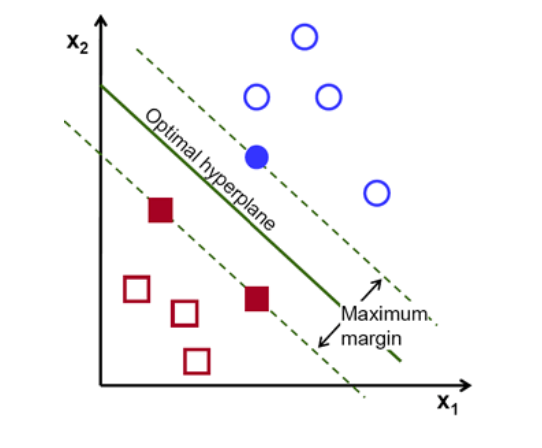
SV(supprot vector)를 의미하는 것은 각 class의 경계에 해당하는 데이터들을 의미.
그것보다는 maximum margin을 갖고 있는hyperplanes. margin이 최대가 되도록 하는 가운데 선을 찾으려고 하고 그리고 이때 계산에 쓰이는 것들은 svm이 사용.경계 뒤 데이터에 대해서는 뒤쪽은 계산을 포함하지 않는다.
입력으로 들어오는 인풋 input sample features, 그에대한 결과는 y(output)
SVM을 running하는 과정에서 얻어내는 것은 weight들.
그리고 이것으로 선 y를 predict하는데 사용.
margin을 최대하게 optimize한다.
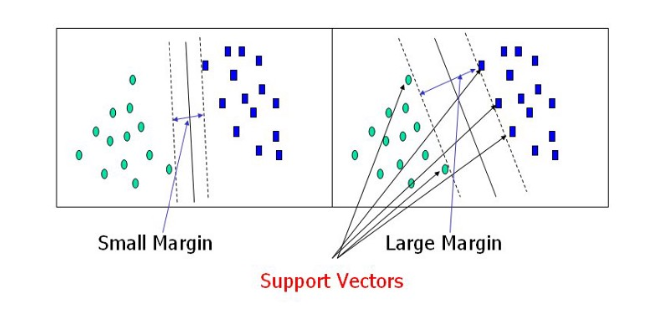
Nonzero weights를 통해 support vectors.
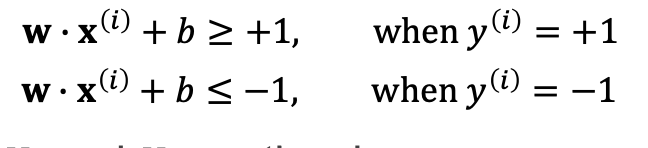
SVM에서 =1, =-1로 정의를 하는데 margin이 최대가 되도록!
1보다 크다 -1보다 작다는 그 class안에 존재한다는 것을 의미.
다른 vector는 신경쓰지 않는다. The decision boundary 즉 1과 -1의 경계에 해당하는 support vector만을 신경쓴다.
전체식을보면 가운데 선을 보면 h0와 h1둘 사이의 거리를 보면 어떠한 선분에서 점까지의 거리가 일정하다. 따라서 distance = 2/절댓값w(weight)라고 정리할 수 있고 distance의 최대는 결국 2/w의 최대, 그리고 곧 weight. 즉, w의 최소를 의미합니다.
결국 그 page를 정리하면 y=1일때, w내적x + b >=1, y=-1일때, w내적x +b <= -1 이고, 두식을 합쳐서 표현하면 y(w내적x + b) >= 1 로 표현할 수 있습니다.
5page부터, 30분 51초 76부터…이어서…
weight를 minimize하는데 지켜야 되는 조건은 class를 유지해야되는 조건
즉,support vector조건을 만족하면서 범위 안에서의 weight를 minimize하는 식을 완성
sign만 알고있으면 1보다크면, -1보다 작으면 의 조건을 만족하도록, 이를 constrained optimization problem(라그랑주 이용)으로 바꾼다.
즉, 다음과 같은 식으로 표현될 수 있다.
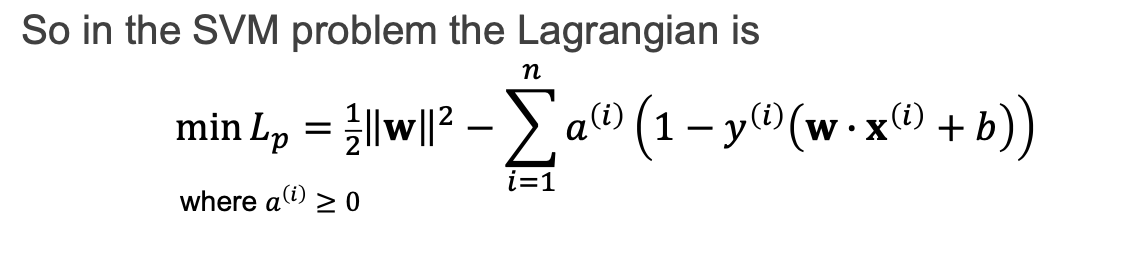
미분해서 0이되는 지점을 찾으면 된다. f는 제곱으로 처리, 형식을 맞출 용도로 식을 구성한 것임.
묶어놓고 같이 minimize
cost함수를 만들려면 hard-margin SVM
Soft-margin SVM 서로 섞인 outlier가 하나도 없을 때 hard margin. x들사이에 o가 있을때 이런것들이 outlier 즉 오차라고 볼 수 있고 오차를 포함해서 간다는 형태가 soft-margin.
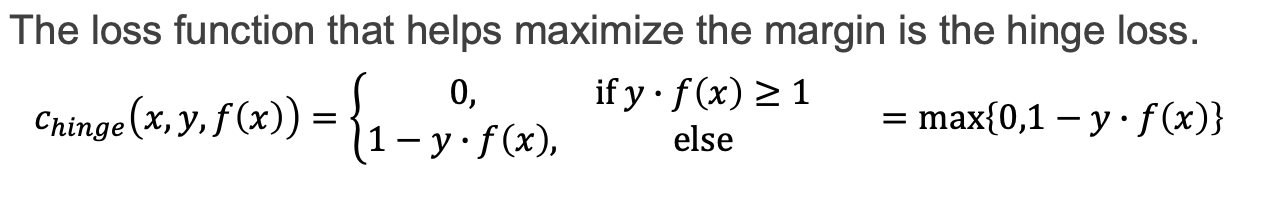
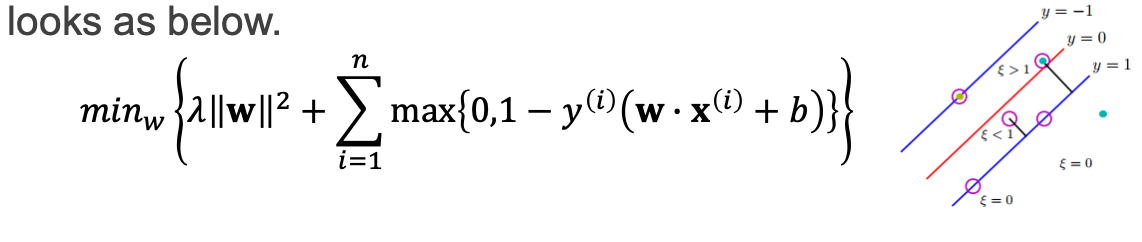
Hinge lose에서는 loss -> y에다가 f(x)곱한게 1보다 크면 즉,class 안에 존재한다면 loss값은 0, 그 외에 그렇지 않을때는 loss값을 계산해야한다. error값을 포함해야 한다. 최종적으로 묶어서 쓴식은 다음과 같은데 0과 1사이에서
weight를 최소화 하는게 목표.(촤종적 목표)
Gradient updates
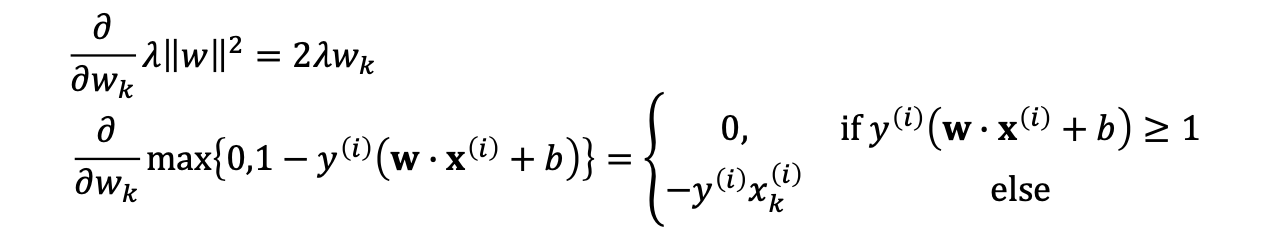
classifaction의 상황일때
->답을 맞췄을 때 (w에 대한 미분)(x도 없고 y도 없으므로 그냥 w만 줄이기만 하면됌;)
Miss classificatoin (위에 식의 상황)
->답을 틀렸을떄 predict가 틀렸을 때(입력과 출력을 포함시켜서 빼주는 과정)
틀리면 계산량이 많이 늘음. (아래 식의 상황)
그리고 miss classification의 상황에 대한 weight와 bias의 update를 정리한 식은 또한 다음과 같습니다.
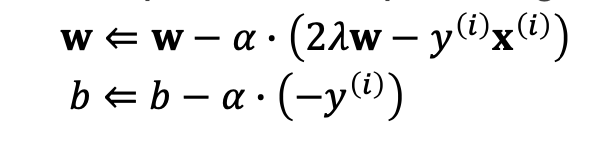
Linear 와 non-linear SVM
계산이 linear regression은 층 하나.
Non-linear는 층이 여러개
svm은 한 층으로 계산하기를 원함. 따라서 non-linear인경우 kernel 함수를 사용.
nn에서는 non-linear는 쌓으면 가능했으나
svm에서는 차원을 늘려서 해결한다.
svm에서 양쪽으로 다른 클래스가 있을 때는 둘을 구분하기 힘듦. 라인을 통째로 2차원에 mapping
그러고 나서 자를 수 있어짐 (그냥 x일때는 가능하지 못했음.) 차원이 많아진다-> feature spaces를 늘린다. 차원을 높이면 x도 변하지만 y도 바뀜.
(아래 그림 참조)
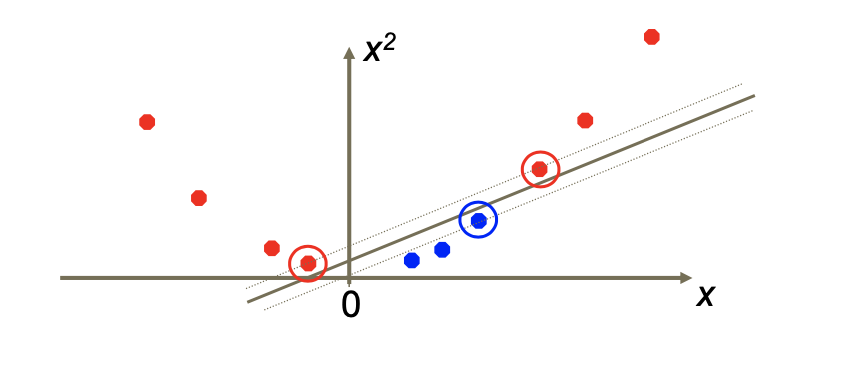
(classification이 잘 안되었을 때)
차원은 features에 비례, 그래서 차원 개수가 생각보다 클 수 있음.
그런데 이때 차원을 늘리면서 계산량이 너무 늘어나는 문제 -> 따라서 kernel trick을 사용.
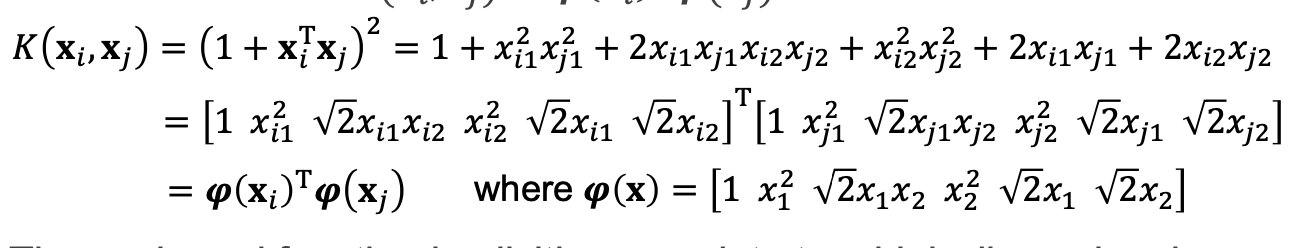
위의 식을 정리하자면 x와 y를 곱해서 내적 후 1 더하고 제곱하는 과정.(2차원) 정리하면 새로운 변수와 그에 대한 전치.(파이(x))그러면 차원을 늘리는 과정이 아님.(계산량에 대한 issue를 해결할 수 있음.)-> 이렇게 kernel trick을 사용하면 더 좋개 나올 확률이 있음.
Kernel function종류
linear(아무것도 안함)
Power,
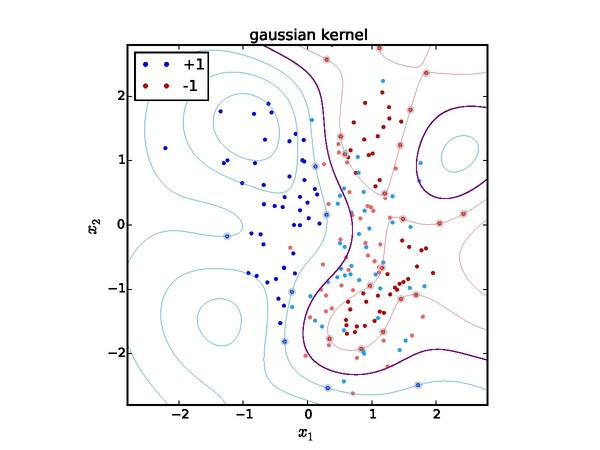
Gaussian
그과정을 보면 mapping을 해서 한 결과와 kernel function을 통해 도출한 결과가 동일해야한다.
Higher-dimensional space
원래 차원의 특징을 고대로 갖고 있으면서 차수를 늘리는 과정.계산은 적게 하면서 non-linear한 경우도 효과적으로 결과를 낼 수 있게하는 것.
svm의 장점
맞는 kernel함수를 사용자가 적용시켜야하며 그 결과가 성공적으로 안나올 수 있다.(case by case)
데이터셋에 대한 제한이 적다.
계산량이 작다.
svm의 단전
양질의 데이터셋이 존재한다면 따로 신경쓸 필요가 없는 딥러닝이 더 편함.
더 복잡한, 더 새로운 문제에 대해서의 적용이 더 쉬움
kernel함수를 제대로 잘 찾을 수 있어야함.
간단한, svm으로 잘 처리할 수 있는 것을 굳이 딥러닝으로 처리할 필요가 없음.
참고자료)
광운대학교 인공지능프로그래밍 수업 handout
