2장 딥러닝의 동작 원리
선형회귀(LinearRegression)
딥러닝에서 모델을 만든다는 것은 classification을 하기 위한 예측선을 긋는 것이라고 했는데 이에 쓰이는 가장 기본적인 2가지 계산 원리가 바로 선형 회귀(LinearRegression)와 로지스틱 회귀(LogisticRegression)입니다.
y=f(x)라는 간단한 함수식이 딥러닝에도 적용 되는데, 이때 input값으로 들어가는 정보들은 결과에 대한 이유이자 '독립변수' 입니다. 그리고 그 결과로 나오는 output값들은 x에 따라 달라지는 결과이자 '종속변수' 입니다. 그리고 하나의 x값만으로도 y값을 설명할 수 있는 것을 '단순 선형 회귀', x값이 여러 개 필요할 떄는 '다중 선형 회귀'입니다.
그리고 선형 회귀에서의 예측선은 일차함수 그래프이고 이를 y=ax+b라고 표현할 수 있고,
이때 a는 기울기 값, b는 y절편값 입니다.
그리고 이때 a와 b값을 구하는데 사용하는 방법이 최소제곱법이며,
a = (x-x의 평균)(y-y의 평균)의 합/(x-x의 평균)의 합의 제곱
b = y의 평균 - x의 평균x기울기 a
참고가 되는 코드는 다음과 같습니다.
import numpy as np
# x 값과 y값(임의의 값 설정)
x=[2, 4, 6, 8]
y=[81, 93, 91, 97]
# x와 y의 평균값
mx = np.mean(x)
my = np.mean(y)
print("x의 평균값:", mx)
print("y의 평균값:", my)
# 기울기 공식의 분모 : (x-x의 평균)의 합의 제곱
divisor = sum([(mx - i)**2 for i in x])
# 기울기 공식의 분자 : (x-x의 평균)*(y-y의 평균)의 합
def top(x, mx, y, my):
d = 0
for i in range(len(x)):
d += (x[i] - mx) * (y[i] - my)
return d
dividend = top(x, mx, y, my)
print("분모:", divisor)
print("분자:", dividend)
# 기울기와 y 절편 구하기
a = dividend / divisor
b = my - (mx*a)
위와 같이 처음 구한 a와 b로 구성된 경계선을 수정하는 과정을 또한 이후에 진행해야 하는데
이때 사용하는 방법은 '평균 제곱근 오차'라는 방법 입니다.
'오차 = 실제 값- 예측 값'을 의미하고, 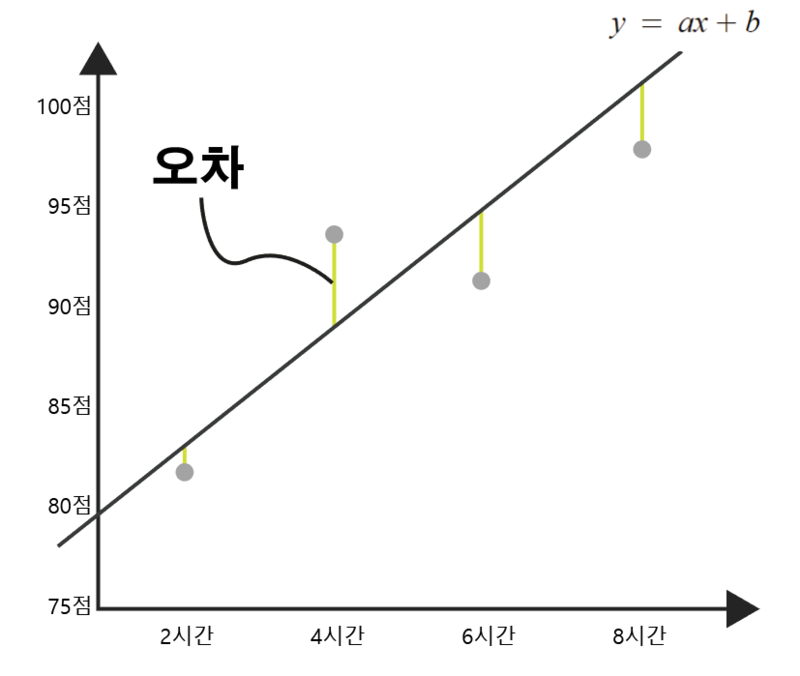
오차는 실제로 절댓값을 반영해야 하는데 그때문에 오차의 제곱의 합, 그리고 이에 대한 평균
즉, 평균 제곱 오차(MSE)
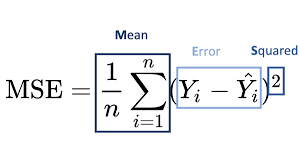
그리고 이 값이 사용하기에 너무 크기 때문에 제곱근을 씌운
평균 제곱근 오차(RMSE)
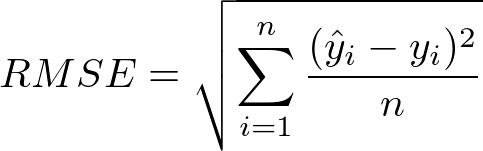
참고가 되는 코드는 다음과 같습니다.
#-*- coding: utf-8 -*-
import numpy as np
# y=ax + b에 a,b 값 대입하여 결과를 출력하는 함수
def predict(x):
return ab[0]*x + ab[1]
# RMSE 함수
def rmse(p, a):
return np.sqrt(((p - a) ** 2).mean())
# RMSE 함수를 각 y값에 대입하여 최종 값을 구하는 함수
def rmse_val(predict_result,y):
return rmse(np.array(predict_result), np.array(y))
이후에 경사하강법은 기울기에 대한 오차에 대한 그래프가 convert한 형태로 미분가능한 형태(2차함수 그래프)로 표현될 때 미분해서 0이되는 지점에서의 기울기가 오차가 최소가 되게하는 기울기이므로 이를 반영 합니다.
위 과정을 순서에 따라 보면 다음과 같이 설명할 수 있는데
1)임의의 기울기(a1) 지점에서의 순간변화율을 구한다.
2)구해진 기울기의 반대 방향일때의에 해당하는 또 다른 기울기(a2)에서의 순간변화율을 구한다
3)임의의 기울기(a3) 지점에서의 순간변화율을 구한다.
위 과정을 반복합니다.
이때 임의의 기울기 지점의 변화정도를 학습률 즉, learning rate라고 하는데 이 step이 너무 크면 a값이 한점에 모이지 않고 발산하게 됩니다.
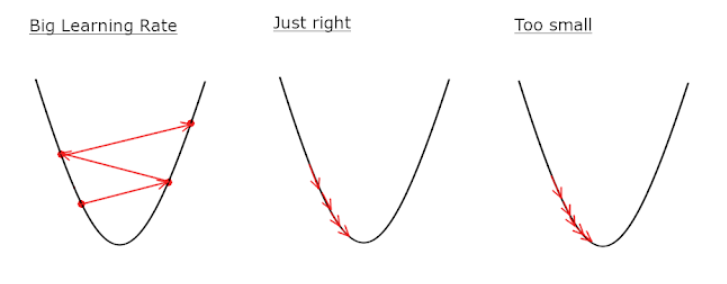
참고가 되는 코드는 다음과 같습니다.
# y에 대한 일차 방정식 ax+b의 식을 세운다.
y = a * x_data + b
# 텐서플로 RMSE 함수
rmse = tf.sqrt(tf.reduce_mean(tf.square( y - y_data )))
# 학습률 값
learning_rate = 0.1
# RMSE 값을 최소로 하는 값 찾기
gradient_decent = tf.train.GradientDescentOptimizer(learning_rate).minimize(rmse)다중 선형 회귀는 단일 선형 회귀에서 x2변수와 a2 변수를 추가해서
y=a1x1+b 라는 식에서 y=a1x1+a2*x2+b와 같은 식이 되도록 합니다.
로지스틱 회귀(LogisticRegression)
참과 거짓 판단장치로는 로지스틱 회귀 방법이 있습니다.
즉 결과를 one-hot encoding하여서 1과 0으로 binary하게 표현하는 것임을 예상할 수 있습니다.
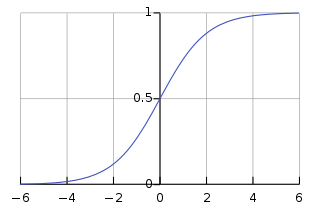
위와 같은 그래프 중 최적화된 함수 식은 시그모이드 함수인데
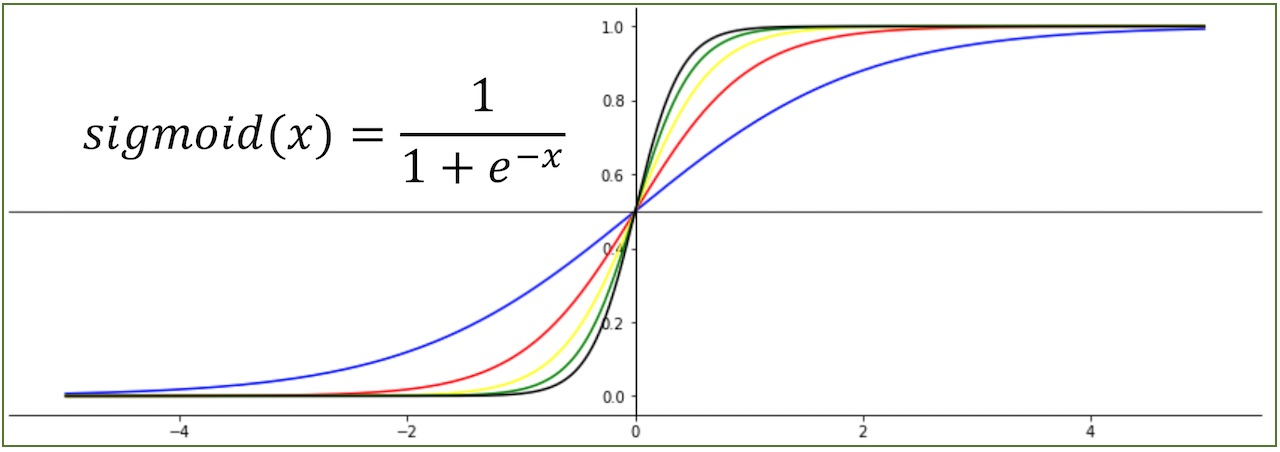
a값이 클수록 기울기가 커지는 것을 알 수 있습니다.
그리고 위의 선형 회귀 처럼 a와 b 값을 구하기 위해 예측 값에 대한 오차를 그래프로 나타내면 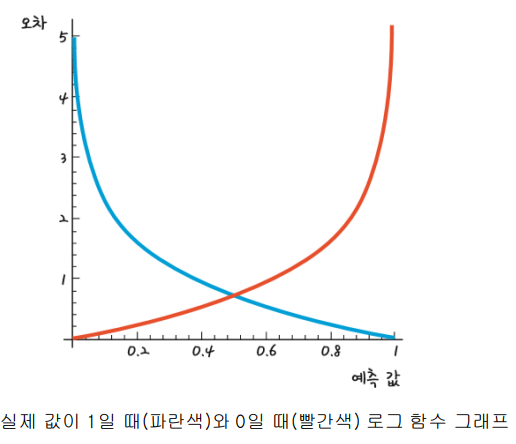
다음과 같고,그래프에 대한 식을 나타내면 다음과 같습니다.
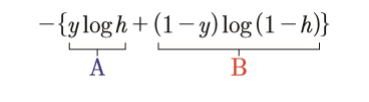
참고가 되는 코드는 다음과 같습니다.
# y 시그모이드 함수의 방정식을 세움
y = 1/(1 + np.e**(a * x_data + b))
# loss를 구하는 함수
loss = -tf.reduce_mean(np.array(y_data) * tf.log(y) + (1 - np.array(y_data)) * tf.log(1 - y))
# 학습률 값
learning_rate=0.5
# loss를 최소로 하는 값 찾기
gradient_decent = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss)
다중 로지스틱 회귀는 앞서서 언급한 다중 선형 회귀 처럼 변수와 기울기 값을 추가하면 됩니다.
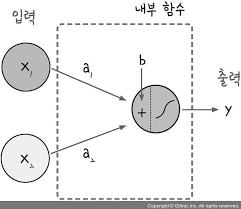
그리고 위와 같은 로지스틱회귀를 뉴런의 퍼셉트론으로 표현 할 수 있는데 그림으로 표현하면 다음과 같습니다.
첨부된 자료 출처
https://ang-love-chang.tistory.com/25
https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=jihoons8193&logNo=221241897792
https://taewanmerepo.github.io/2017/09/sigmoid/post.jpg
https://ko.wikipedia.org/wiki/%EB%A1%9C%EC%A7%80%EC%8A%A4%ED%8B%B1_%ED%9A%8C%EA%B7%80
참고한 자료 출처
https://github.com/gilbutITbook/006958
<모두의 딥러닝> (길벗출판사)
