인간의 뇌 안에서 뉴런과 뉴런사이 시냅스라는 연결 부위를 통해 전위가 임계 값을 넘으면 신호를 전달하는데,이 매커니즘은 앞서 배운 "로지스틱 회귀"와 많이 닮은 것을 알 수 있습니다.
즉 신경망을 이루는 가장 중요란 기본 단위는 "퍼셉트론"인데, 이때 퍼셉트론은 입력 값과 활성화 함수를 사용해 출력 값을 다음으로 넘기는 가장 작은 신경망 단위입니다.
그리고 위에서 언급한 것과 같이 로지스틱 회귀가 곧 퍼셉트론의 개념이라고 생각할 수 있는데, 이를 식으로 표현하면 다음과 같습니다. y=wx+b(w는 가중치,b는 바이어스) 그리고 이 식에서의 y값 즉, 입력값(x)와 가중치(w)의 곱을 모두 더한 다음 거기에 바이어스(b)를 더한 값을 가중합이라고 합니다. 그리고 가중합의 결과를 놓고 1 또는 0을 출력해서 다음으로 보냅니다. 여기서 0과 1을 판단하는 함수가 활성화 함수이고, 앞서 배웠던 시그모이드 함수가 대표함수라고 할 수 있습니다.
그런데 앞서 배운 선형 회귀와 로지스틱 회귀를 통해 결국 선이나 2차원 평면을 그리는 작업 즉,선을 긋는 작업을 진행하는데 이때 'XOR'문제는 해결되지 않는 상황입니다.따라서 이를 해결한 개념이 바로 '다층 퍼셉트론'입니다. 즉 앞서 2차원 평면을 3차원으로 바꾸어 이를 해결하였습니다. 그리고 이와 같은 작업을 가능하게 하기 위해서는 은닉층(hidden layer)을 만들면 되는데,input값들의 영역이 n차원에서는 곡선이거나 해결 불가능이었는데 차원의 수를 N(N>n)로 늘리는 과정을 통해 두 영역을 가로지르는 선을 직선으로 바꾸는 과정을 진행합니다.

위의 그림애서 볼 수 있듯이 은닉층의 각 노드를 기준으로 식을 계산합니다.
가운데 숨어있는 은닉층으로 퍼셉트론이 각각 자신의 가중치(w)와 바이어스(b)값을 보내고, 이 은닉층에서 모인 값이 한 번 더 시그모이드 함수를 통과시켜 최종 값으로 결과를 보냅니다.
n1(은닉층의 위에서 첫번째 노드)= 시그마(x1w11+x2w12...+xn*w1n+b1)
그리고 위의 식에서 n1,n2...n4에서 y1과 ym에 보내지는 값을 위와 같은 방식으로 다시한번 계산합니다.
이와 같은 '다층 퍼셉트론'방법으로 앞선 '퍼셉트론'방법에서 해결하지 못했던 'XOR'문제를 해결할 수 있는데, 입력층과 은닉층 사이에서 'NAND'와 'OR'를 작동시키고 은닉층과 출력층에서는 'AND'gate를 구조로 하여 통과시키는 방법으로 'XOR'문제를 해결할 수 있습니다.
import numpy as np
# 퍼셉트론
def MLP(x, w, b):
y = np.sum(w * x) + b
if y <= 0:
return 0
else:
return 1
# NAND 게이트
def NAND(x1,x2):
return MLP(np.array([x1, x2]), w11, b1)
# OR 게이트
def OR(x1,x2):
return MLP(np.array([x1, x2]), w12, b2)
# AND 게이트
def AND(x1,x2):
return MLP(np.array([x1, x2]), w2, b3)
# XOR 게이트
def XOR(x1,x2):
return AND(NAND(x1, x2),OR(x1,x2))
처음 모델의 식을 완성할 때의 가중치를 구하는 방법은 '경사하강법'을 이용합니다. 그런데 은닉층과 같은 숨어 있는 층이 하나 더 생겼을 때는 앞선 경사하강법을 통해 구한 식을 통과한 결과 값을 이용하여, 다시말해 단일 퍼셉트론에서 결과값을 얻으면 이를 이용하여 오차를 구해 이를 토대로 앞 단계에서 정한 가중치를 조정하는 과정을 거칩니다.
식으로 보면 'W(t+1) = W(t)-σ오차/σW'이며, 새 가중치는 헌 가중치에서 '가중치에 대한 기울기'를 뺀 값.
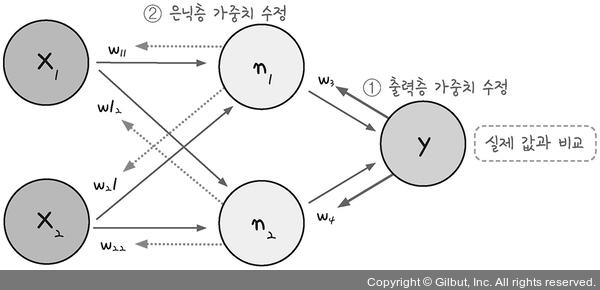
즉, 입력에서 출력까지의 과정의 역순으로 오차를 수정하는 과정을 거치게 됩니다. 다층 퍼셉트론에서의 최적화 과정 즉, '오차 역전파'의 구동방식을 정리하면 다음과 같습니다.
1) 임의의 초기 가중치(W1)를 준 뒤 결과(Yout)을 계산합니다.
2) 계산 결과(측정 값)과 우리가 원하는 값(예상 값)사이의 오차를 구합니다.
3) 경사하강법을 이용해 바로 앞 가중치를 오차가 작아지는 방향으로 업데이트 합니다.
4) 1)~3)의 과정을 더이상 오차가 줄어들지 않을 때까지 반복합니다.
오차역전파 계산은 다음 동영상을 통해 이해하면 더 도움이 되었습니다.
("혁펜하임"님의 딥러닝 강의 중 backpropagation강의)
https://youtu.be/aUd2MKLvDsc?si=9nfXon8pGqYCgIWY
간단히 오차역전파에 필요한 계산과정을 보면 W(t+1) = W(t)-σ오차/σW'에서 'σ오차/σW'에서 편미분 즉, 분모의 변수에 관해 분자의 식을 미분을 한다는 뜻이며, 오차 Yout 안에는 두개(Yo1,Yo2)의 출력 값이 있는데 이 값을 예측 값이라고 하고, 출력값을 각각(Yt1,Yt2)라고 하면 오차Yo1 = 1/2(Yt1-Yo1)^2, 오차Yo2 = 1/2(Yt2-Yo2)^2 로 표현할 수 있습니다.
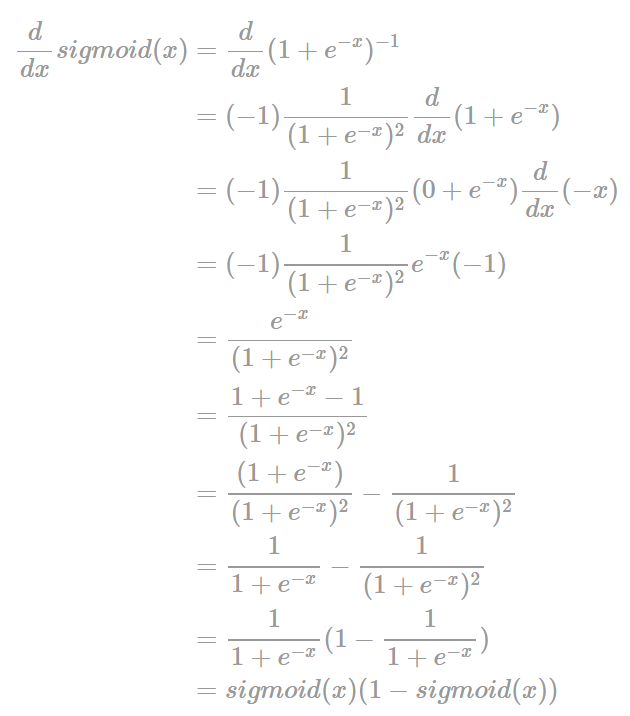
그리고 편미분시 체인룰에 의해 미분과정을 거쳐 최종적인 델타 식으로 업데이트 된 오차에 대한 식을 정리하면 다음과 같습니다.
출력층의 오차 업데이트 = (Yo1-Yt1)Yo1(1-Yo1)Yh1
은닉층의 오차 업데이트 = (δYo1Yo1+δYo2Yo2)Yh1(1-Yh1)*X1
으로 정리할 수 있습니다. 사실 두 식 모두 형태의 복잡성이 있을 뿐 본질 적으로는 out(1-out)의 형태인 것을 알 수 있습니다.
# -*- coding: utf-8 -*-
import random
import numpy as np
random.seed(777)
# 환경 변수 지정
# 입력값 및 타겟값
data = [
[[0, 0], [0]],
[[0, 1], [1]],
[[1, 0], [1]],
[[1, 1], [0]]
]
# 실행 횟수(iterations), 학습률(lr), 모멘텀 계수(mo) 설정
iterations=5000
lr=0.1
mo=0.9
# 활성화 함수 - 1. 시그모이드
# 미분할 때와 아닐 때의 각각의 값
def sigmoid(x, derivative=False):
if (derivative == True):
return x * (1 - x)
return 1 / (1 + np.exp(-x))
# 활성화 함수 - 2. tanh
# tanh 함수의 미분은 1 - (활성화 함수 출력의 제곱)
def tanh(x, derivative=False):
if (derivative == True):
return 1 - x ** 2
return np.tanh(x)
# 가중치 배열 만드는 함수
def makeMatrix(i, j, fill=0.0):
mat = []
for i in range(i):
mat.append([fill] * j)
return mat
# 신경망의 실행
class NeuralNetwork:
# 초깃값의 지정
def __init__(self, num_x, num_yh, num_yo, bias=1):
# 입력값(num_x), 은닉층 초깃값(num_yh), 출력층 초깃값(num_yo), 바이어스
self.num_x = num_x + bias # 바이어스는 1로 지정(본문 참조)
self.num_yh = num_yh
self.num_yo = num_yo
# 활성화 함수 초깃값
self.activation_input = [1.0] * self.num_x
self.activation_hidden = [1.0] * self.num_yh
self.activation_out = [1.0] * self.num_yo
# 가중치 입력 초깃값
self.weight_in = makeMatrix(self.num_x, self.num_yh)
for i in range(self.num_x):
for j in range(self.num_yh):
self.weight_in[i][j] = random.random()
# 가중치 출력 초깃값
self.weight_out = makeMatrix(self.num_yh, self.num_yo)
for j in range(self.num_yh):
for k in range(self.num_yo):
self.weight_out[j][k] = random.random()
# 모멘텀 SGD를 위한 이전 가중치 초깃값
self.gradient_in = makeMatrix(self.num_x, self.num_yh)
self.gradient_out = makeMatrix(self.num_yh, self.num_yo)
# 업데이트 함수
def update(self, inputs):
# 입력 레이어의 활성화 함수
for i in range(self.num_x - 1):
self.activation_input[i] = inputs[i]
# 은닉층의 활성화 함수
for j in range(self.num_yh):
sum = 0.0
for i in range(self.num_x):
sum = sum + self.activation_input[i] * self.weight_in[i][j]
# 시그모이드와 tanh 중에서 활성화 함수 선택
self.activation_hidden[j] = tanh(sum, False)
# 출력층의 활성화 함수
for k in range(self.num_yo):
sum = 0.0
for j in range(self.num_yh):
sum = sum + self.activation_hidden[j] * self.weight_out[j][k]
# 시그모이드와 tanh 중에서 활성화 함수 선택
self.activation_out[k] = tanh(sum, False)
return self.activation_out[:]
# 역전파의 실행
def backPropagate(self, targets):
# 델타 출력 계산
output_deltas = [0.0] * self.num_yo
for k in range(self.num_yo):
error = targets[k] - self.activation_out[k]
# 시그모이드와 tanh 중에서 활성화 함수 선택, 미분 적용
output_deltas[k] = tanh(self.activation_out[k], True) * error
# 은닉 노드의 오차 함수
hidden_deltas = [0.0] * self.num_yh
for j in range(self.num_yh):
error = 0.0
for k in range(self.num_yo):
error = error + output_deltas[k] * self.weight_out[j][k]
# 시그모이드와 tanh 중에서 활성화 함수 선택, 미분 적용
hidden_deltas[j] = tanh(self.activation_hidden[j], True) * error
# 출력 가중치 업데이트
for j in range(self.num_yh):
for k in range(self.num_yo):
gradient = output_deltas[k] * self.activation_hidden[j]
v = mo * self.gradient_in[j][k] - lr * gradient
self.weight_in[j][k] += v
self.gradient_out[j][k] = gradient
# 입력 가중치 업데이트
for i in range(self.num_x):
for j in range(self.num_yh):
gradient = hidden_deltas[j] * self.activation_input[i]
v = mo*self.gradient_in[i][j] - lr * gradient
self.weight_in[i][j] += v
self.gradient_in[i][j] = gradient
# 오차의 계산(최소 제곱법)
error = 0.0
for k in range(len(targets)):
error = error + 0.5 * (targets[k] - self.activation_out[k]) ** 2
return error
# 학습 실행
def train(self, patterns):
for i in range(iterations):
error = 0.0
for p in patterns:
inputs = p[0]
targets = p[1]
self.update(inputs)
error = error + self.backPropagate(targets)
if i % 500 == 0:
print('error: %-.5f' % error)
# 결괏값 출력
def result(self, patterns):
for p in patterns:
print('Input: %s, Predict: %s' % (p[0], self.update(p[0])))
if __name__ == '__main__':
# 두 개의 입력 값, 두 개의 레이어, 하나의 출력 값을 갖도록 설정
n = NeuralNetwork(2, 2, 1)
# 학습 실행
n.train(data)
# 결괏값 출력
n.result(data)
# Reference: http://arctrix.com/nas/python/bpnn.py (Neil Schemenauer)
그런데 이렇게 층을 쌓으면서 출력층까지 쌓은 신경망을 보면 층이 늘어나면서 기울기가 중간에 0이 되어버리는 기울기 소실 문제가 발생하기 시작했습니다.
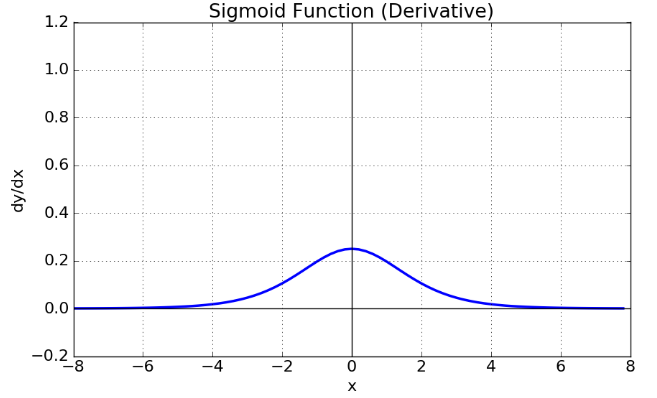
이와 같은 문제가 발생한 이유는 시그모이드 함수의 특성 때문에 시그모이드를 미분한 값들을 모으면 종을 뒤집은 듯한 그래프로 표현되며 이는 시간이 갈수록 즉, 층을 거쳐 갈수록 기울기가 사라져 가중치를 정하기가 어려워지는 것입니다.
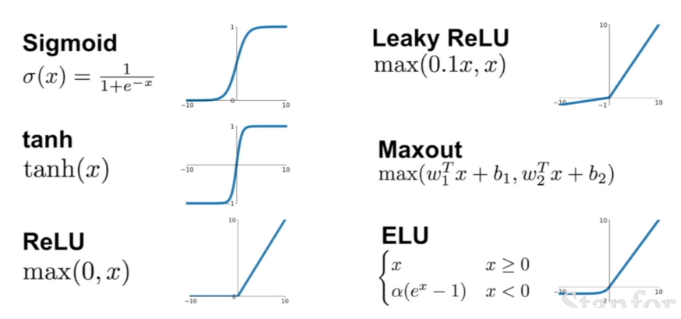
따라서 이와 같은 문제를 해결하기 위해 다른 많은 활성화 함수가 고안되었으며 현재 가장 많이 사용되는 활성화 함수는 ReLU함수입니다.
속도와 정확도 문제를 해결하는 고급 경사 하강법을 보면 층을 쌓아서 계산하는 방법(NN,NeuralNetwork)를 사용하므로 전체 데이터를 미분해야 하므로 계산량이 매우 많다는 단점이 있습니다.
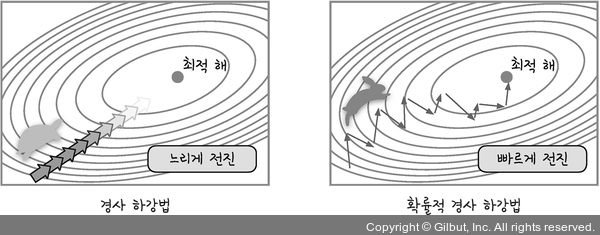
따라서 계산량에 따라 속도가 느려지는데 이러한 단점을 보완하는 방법으로 전체데이터를 사용하지 않고 랜덤하게 추출한 일부 데이터를 사용하는 방법을 사용하는데 이때 확률적 경사 하강법(SGD)를 사용하고 이때 추가로 모멘텀 즉, 가속도 개념을 추가하여 적용하여 보다 정확도를 개선합니다.
이와 같이 고급 경사하강법의 종류에는 확률적 경사 하강법(SGD),모멘텀 외에도 네스테로프 모멘텀,아다그리드,알엠에스프롭,아담(Adam)과 같은 것들이 있고
현재 가장 많이 사용되는 고급 경사하강법은 모멘텀과 알엠에스프롭 방법을 합친 방법으로 정확도와 보폭크기가 개선된 방법을 주로 사용합니다.
출처)http://taewan.kim/post/sigmoid_diff/
https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=handuelly&logNo=221824080339
https://thebook.io/080324/0140/
https://mblogthumb-phinf.pstatic.net/MjAxODAzMjhfMjA4/MDAxNTIyMTk3ODQyMzk2.denKdPpRR2e8NQKv93P2B82uaMX1ygVWlyiP29gTnOAg.-Wr1aOLP56BVNZyQ4Yf3R_19k2F5BE25-di6H955my0g.JPEG.msnayana/MLP.jpg?type=w800
<모두의 딥러닝>(길벗출판사)
