Lab04) Logistic Regression
#개인적인 공부를 위한 포스팅이므로 문장들이 잘 정리되어 있지 않습니다.
인공지능 프로그래밍 (230918)
04 선형회귀분석
Correlation(어떤 관계가 있는 일을 확인), regression(추정)
Regression은 값을 추정하는데에 쓰이는 관계를 의미.
correlation과 regresion은 비슷하다고 볼 수 있는데
변수에 대한 상호적 관계를 해석(관계의 정도 즉, 얼마나 밀접한지)
그 관계에 해당하는 값을 알고 싶은것을 "predict"하는 것이라고 볼 수 있습니다.
x(독립변수)에 대해서 y(종속변수)가 어떠한지
위에서 언급했듯이
Regression analysis에서 독립변수와 종속변수를 살펴보면 독립변수는 input으로 생각할 수 있으며,
output은 input에 따라 움직이는 종속변수라고 볼 수 있습니다.
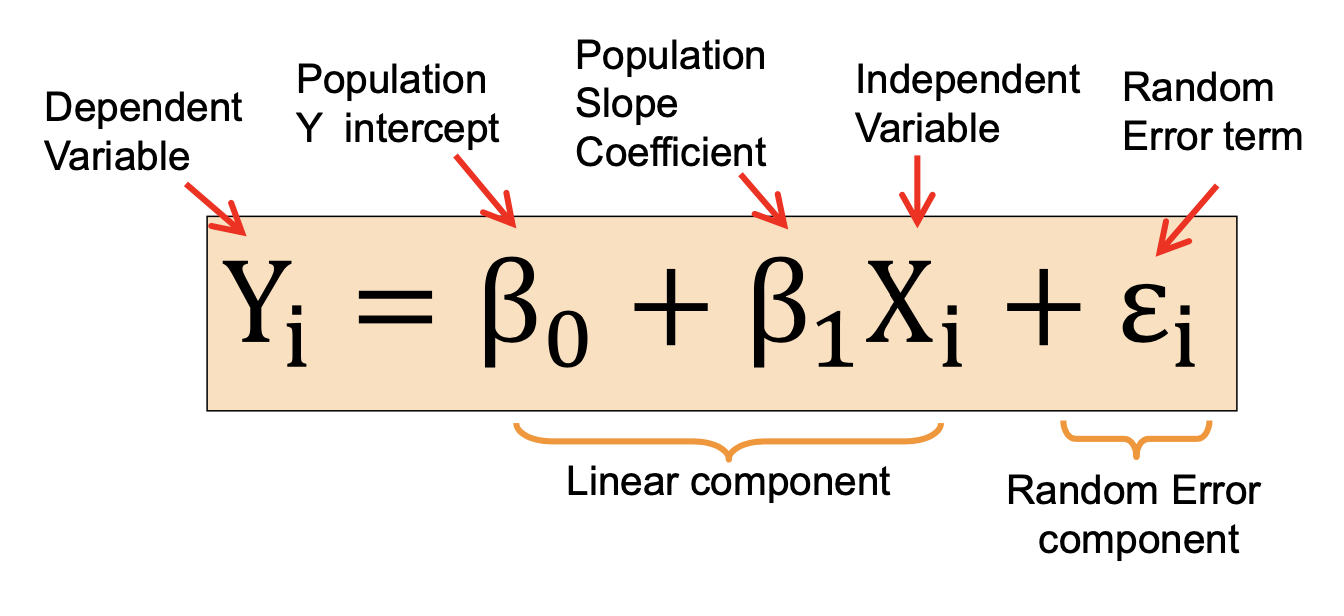
Simple linear regression model
독립변수가 하나일때 설명된다. 식에서
입력에 얼마만큼 비례하냐 -> 배타1
입력이 0일때 나타나는 값 -> 배타0(bias)
Random error term -> 입실론
y는 값.
Linear regression
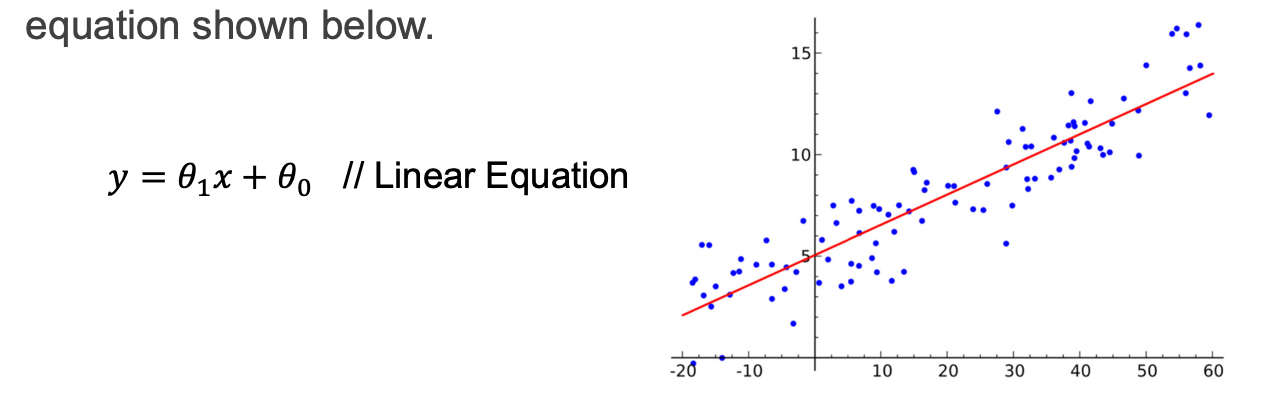
독랍변수와 종속변수의 값들을 점들을 선으로(linear)로 표현하는 것. 사실은 둘다 측정 값들 제어할수 없는 것들.
식으로 봤을 떄는 입력에 의한 출력값 같지만
실제로 점들을 생각했을 때는 x는 실제 측정값들
y는 predict하고 싶었던 값들. 따라서 둘다 알고 있을때 전체 식을 알 수 있음.(coefficient를 구한다.)
이후 model을 사용할때는 식을 통한 y값을 predict가능.
MLE
살제 파라미터를 estimate하는데 쓰이는 것입니다.
에러값에 대해서는 주로 가우시안 분포를 사용. 즉, 정규분포를 사용.
새타0,세타1이 결정되면 x값과 y값이 직선 주변에 나타남(입실론 때문에). 실제 나타나는 y값은 noise에대한 가우시안분포.
실제 나타나는 y값은 확률분포
식에 대해서 설명하면 지수위의 항을 볼 때, 세타1과 세타0의 값을 정확히 알고 있으면 이 항은 0으로 가는 것을 알 수 있습니다. 또한 각 점에 대해서는 독립적일 수 있으나 마치 동전던지기를 했을때 앞면이 나오는 경우를 생각하면 알수 있듯이 2번째일때는 0.5x0.5 = 0.25의 확률이 되는 것과 같은 과정을 거쳐야 합니다. 따라서 식에 이같은 과정이 포함되어서 표현된 것을 알 수 있습니다.
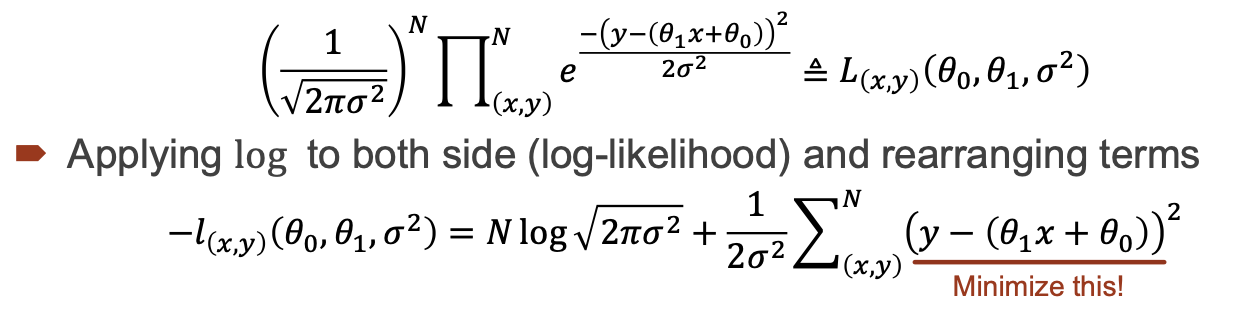
따라서 양변에 log를 씌우면 곱하는 것이 더하는 과정으로 바뀌고 따라서 위에서 언급한 지수위의 항을 minimize하는 형태로 식이 전개되어 갑니다.
Cost function for …
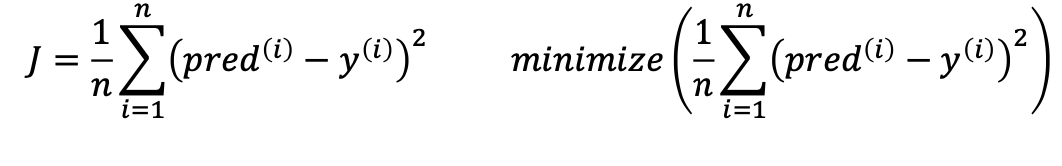
C라고 쓰거나 loss를 minimize하는
J는 자코비안을 의미
각각의 편미분한 값.(=자코비안)
최솟값 구할 때 미분한다.
y값은 측정된 y값
에러가 포함되지 않은값(세타제로,세타 원)에의해서 결정되는 값, pred값. 제대로 진행했다면 에러값은 0으로 간다. 에러를 최소화 하는 형태로..MSE라고 주로 얘기한다.
Gradient descent
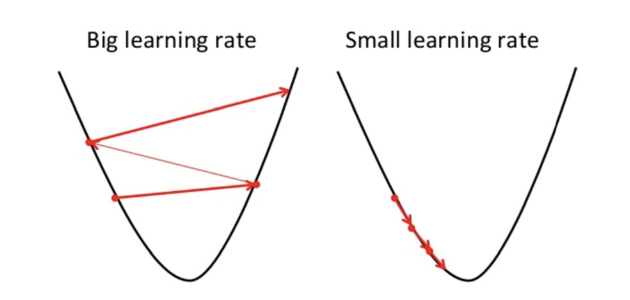
식을 모르는 상태이므로 미분이 잘 안되서 그 해결방법으로 사용하는것 임의의 값에서 일정한 step만큼씩 미분을해서 진행한다.(gradient decent)기울기를 계산, 계속해서 밑으로 내려간다. 그리고 미분이 0일때 값을 최종목적으로 합니다. 최대값을 찾을때는 -값을 붙여서 구하는 (그래프 뒤집기)과정. 값을 작게 잡는것은 계산효율이 떨어지나 정확도의 문제는 없음. 그러나 값(step)을 크게 잡으면 error가 오히려 커지는 경우가 발생할 수도 있음. 즉, 정
확도의 문제가 발생.
step의 크기는 learning rate.
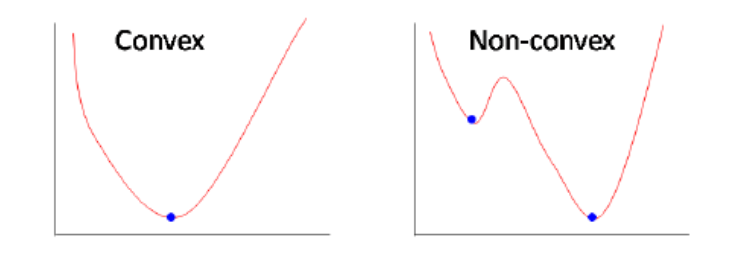
Linear regression -> 두 점을 찍었을 때 두점을 직선으로 연결되면 convex ->최저점이 항상 보인다.그리고 당연히 수렴
중간에 뭐가 걸렸다 싶으면 non-convex. 최저점이 보이지 않는다.
제곱은 convex. 미분의 기울기가 내려가는 쪽으로 각각 미분을 해서 아래로 내려가는 과정을 통해 진행됩니다.
아래 식에 대해서 설명은 각각 편미분하는 과정을 거친다.
기울기를 알면 그 방향으로 진행.
그 방향으로 update를 진행.
원래 세타제로에서 기울기를 반영해서 전체 식을 완성,새로운 세타는 세타제로 - 기울기 알파 곱 세타제이세타제로.
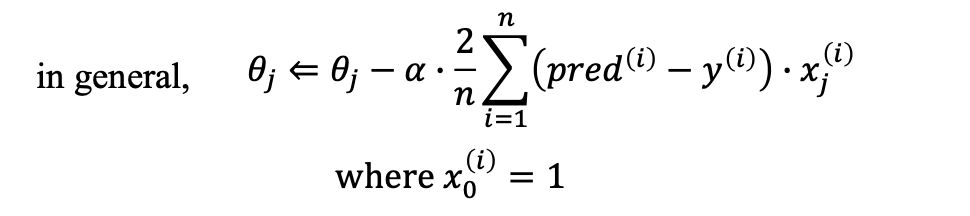
마지막 일반형 식에 대해서도 알 수 있음.
X0 가 항상 1일 때는 bias 항이 사라진(x0는 1) 일반형의 형태 식을 알 수 있음.
Multiple linear regression
다차원의 x
여러개의 multiple independent variables를 모아 둔 최종 식 multiple stands를 볼 수 있고,
h에 대한 식으로 최종적으로 나타낼 수 있는데 y햇,
prediction값(error 항을 빼고 표현)
새타재로는 bias.
뺸것의 제곱의 함의 평균.
여기서 variables->세타들
바꾸고자하는 것들은 즉 변수들은 곧 세타들
learning하고자 하는 variables들은 세타들이다라고 정리.
Multivariate multiple linear regression
입력도 여러개인데 출력도 여러개인 경우.
각각 늘어놓을 수 있음 입출력 둘다 벡터값들.
w는 파라미터.
차원이 바뀌지 않는 것은 w.
parameter는 곧 weight.
Linear 외의 다른 방식으 추론
Logistic regression
Linear regression일 경우에는 1과 0 이진으로 결과가 결정된다. (S커브) decision은 1과 0으로 결정되는 것이 맞으나 미분가능하지않은 함수가 되지 않도록 시그모이드함수를 이용한다. 실제 식은 1이 아닌 임의의 수가 들어갈 수 있으나 현재 표현, 주로 사용하는 함수는 시그모이드 함수를 사용.확률을 로지스틱으로 쓰면 제일 비슷하게 나온다. 가우시안 같이 그 결과가 가장 비슷한 것으로 볼 수 있으며,
미분을 할 수 있다는건 에러가 최소가 될 수 있다는 것을 의미합니다.
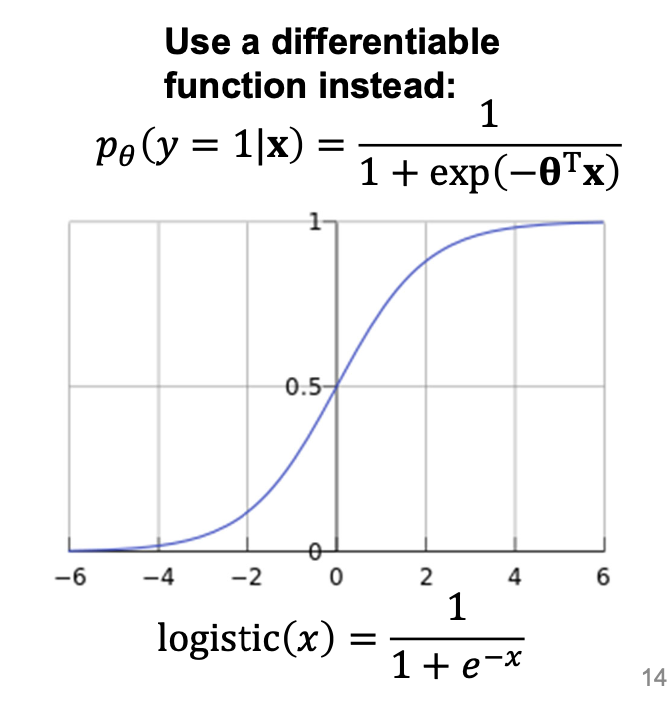
시그모이드 함수에 따르면 양변애 곱이후 식을 정리.
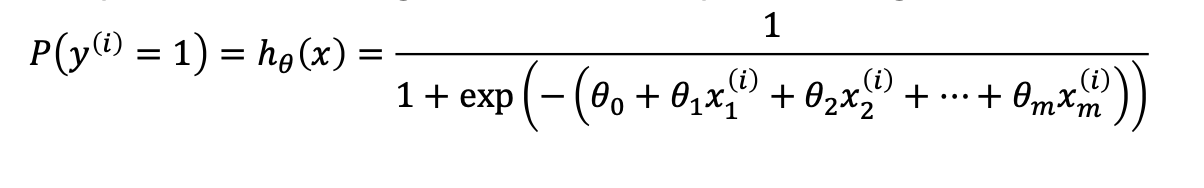
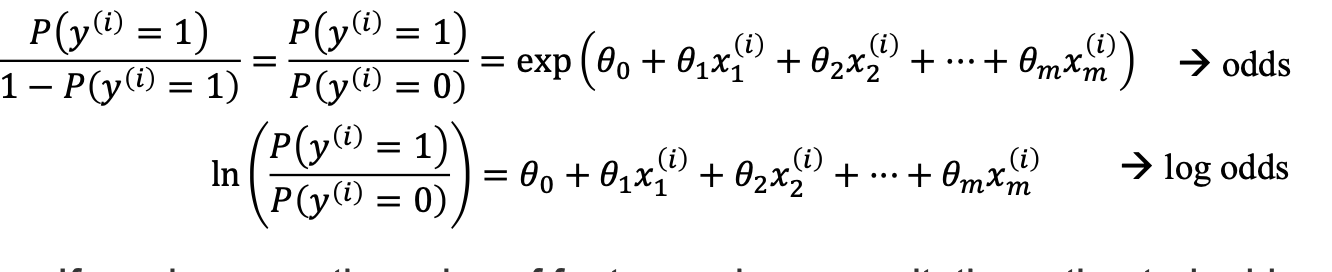
이후 y가 1일 확률을 y가 0일 확률로 나누면 odds (승률)이 나온다.
Log odds로 하면 식이 정리가 된다. 그리고 linear와 logistic을 비교하면 다음과 같다.
따라서 cost function은 log를 걸어서 linear하게 표현하면 다음과 같습니다.
ground truth 는 측정값을 의미 (1이나 0이냐)
Y가 1일때는 앞 항만 남고 0일 떄는 뒷항이 남습니다.이와 같은식을 cross entropy 함수.
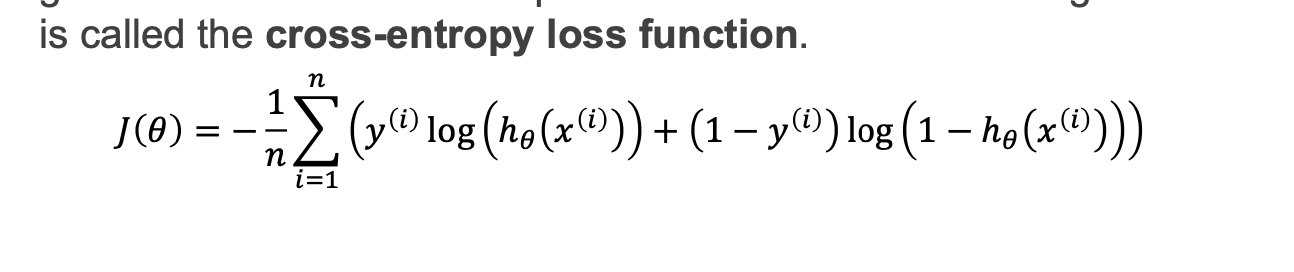
cost함수를 정리하면 다음과 같습니다.
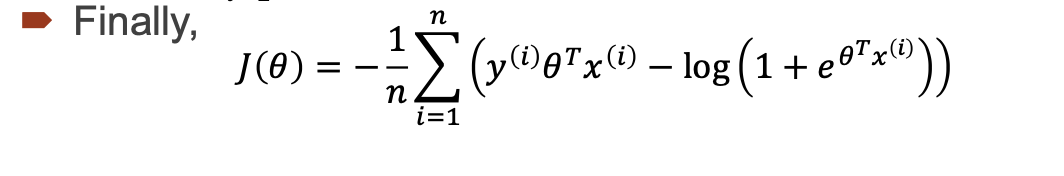
이후 식을 정리할때 세타제이에 대한 미분을 했을 때, 정리된 식은 다음과 같고 시그모이드로 정리 이는 hyper process와 똑같다.
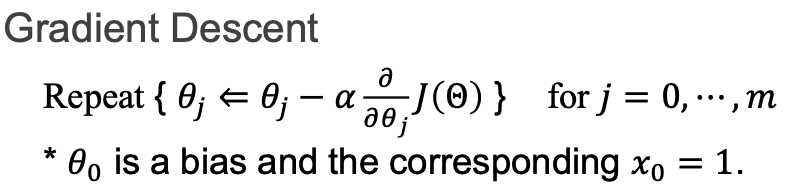
조금씩 조금씩 gradient decent를 반복합니다. 그리고 그 외의 조건으로 세타제로 즉, bias를 따로 설정하거나 x0는 1이라고 하고 식을 정리할 수도 있습니다.
참고자료)
광운대학교 인공지능프로그래밍 수업 handout
