Vision Transformer paper: AN IMAGE IS WORTH 16X16 WORDS: TRANSFORMERS FOR IMAGE RECOGNITION AT SCALE
Vision Transfomer(ViT)
Vision Transfomer(ViT)는 2021년 Google research에서 발표한 모델로, Image classfication 문제에 Transformer 구조를 성공적으로 적용시킨 모델이다.
✏️ ViT의 의의
-
자연어 처리에서 많이 사용되는 Transformer를 전체 아키텍쳐를 크게 변경하지 않은 상태에서 Vision Task에 적용
-
기존의 제한적인 Attention 메커니즘에서 벗어나, CNN구조 대부분을 Transformer로 대체
- 입력(Input)단인 Sequences of Image Patch에서만 제외
-
대용량 데이터셋을 Pre-Train(사전학습) → Small Image 데이터셋(ImageNet-1k, Cifar100)에서 Transfer Learning
- 훨씬 적은 계산 리소스로, 우수한 결과를 얻음
- 단, 많은 데이터를 사전 학습해야 된다는 제한사항 있음
✏️ ViT의 장,단점
✔️ 장점
- Transformer 구조를 거의 그대로 사용하기 때문에 확장성이 좋다. 기존 attention 기반의 모델들은 이론적으로 좋음에도 불구하고 특성화된 attention 패턴 때문에 효과적으로 다른 네트워크에 확장하기가 어려웠다.
- Transformer가 large scale 학습에 우수한 성능이 있다는 것이 검증되었기 때문에 이와 같은 효과를 그대로 얻을 수 있다.
- Transfer learning 시, CNN보다 학습에 더 적은 계산 리소스를 사용한다.
✔️ 단점
- Inductive bias 의 부족으로 인해 CNN보다 데이터가 많이 요구된다.
- Inductive bias는 모델이 처음 보는 입력에 대한 출력을 예측하기 위하여 사용하는 추가적인 가정이라고 할 수 있다. 예를 들어, CNN의 경우 translation equivariance, locality를 가정한다.
- Translation equivariance : 입력 위치가 변하면 출력 또한 위치가 변한다는 것을 가정
- Locality : Convolution 연산을 할 때, 이미지 전체에서 Conv 필터가 이미지의 일부분만 보게 되는데, 이 특정 영역만을 보고 Conv 필터가 특징을 추출할 수 있다는 것을 가정
- 이러한 CNN의 두 가지 가정을 통하여 CNN이 단순한 MLP 모델보다 더 좋은 성능을 낼 수 있다고 해석할 수 있다.
- 반면, Transformer 모델은 attention 구조만을 사용한다. Attention은 CNN과 같이 local receptive field를 보는 것이 아니라, 데이터 전체를 보고 attention할 위치를 정하는 메커니즘이기 때문에, 이 패턴을 익히기 위해서 CNN 보다 더 많은 데이터를 필요로 하게 된다.
- 따라서, 불충분한 데이터 양으로 학습을 하게 되면 일반화 성능이 떨어지게 된다.
- ImageNet과 같은 Mid-size 데이터셋으로 학습 시, ResNet보다 낮은 성능을 보인다.
- 논문에서는 ImageNet-21K나 JFT-300M 데이터셋 처럼 14M~300M 크기의 large scale 데이터 셋으로 사전 학습을 하고 CIFAR100으로 transfer learning을 하였을 때, 높은 정확도를 가짐을 보여준다.
- Inductive bias는 모델이 처음 보는 입력에 대한 출력을 예측하기 위하여 사용하는 추가적인 가정이라고 할 수 있다. 예를 들어, CNN의 경우 translation equivariance, locality를 가정한다.
✏️ ViT 구조
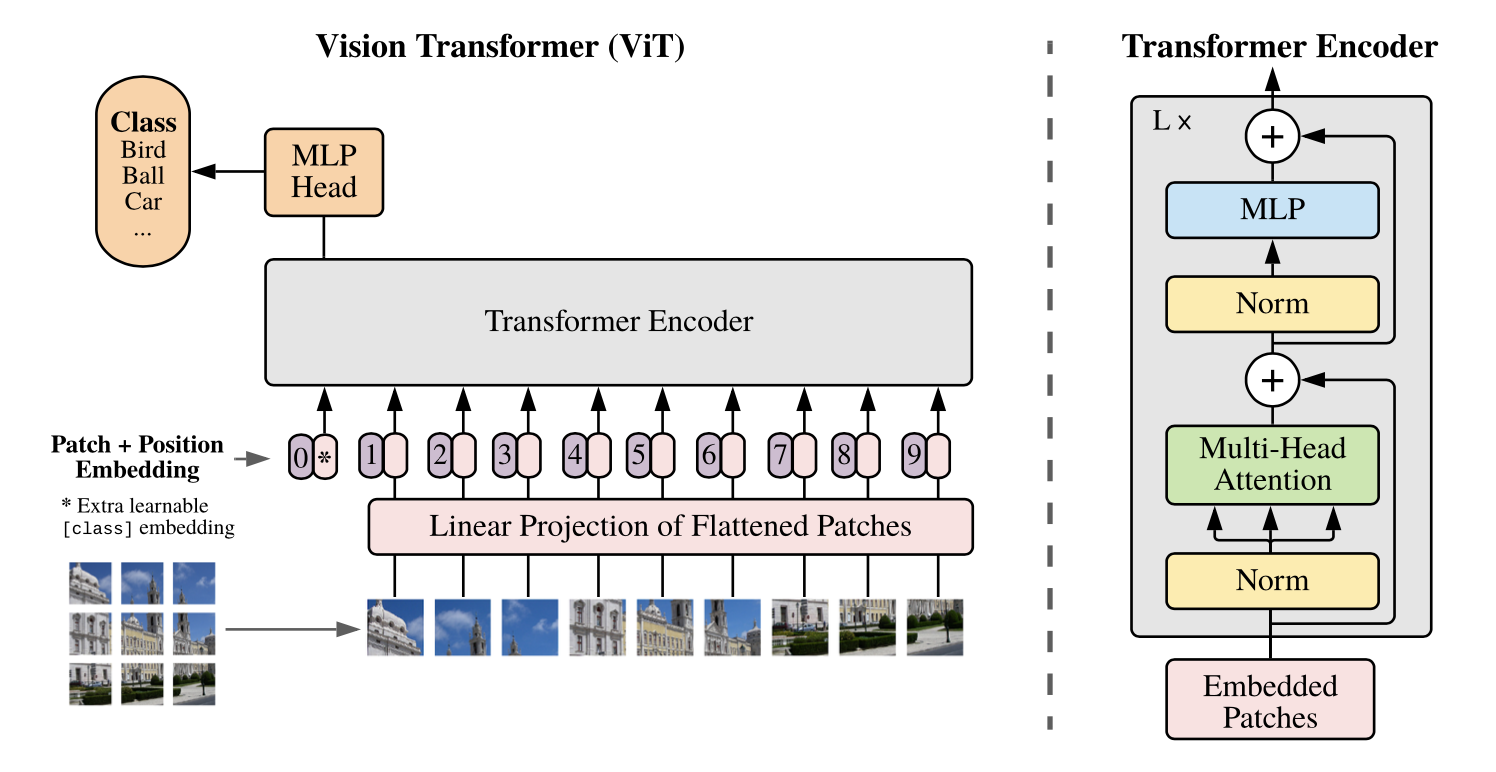
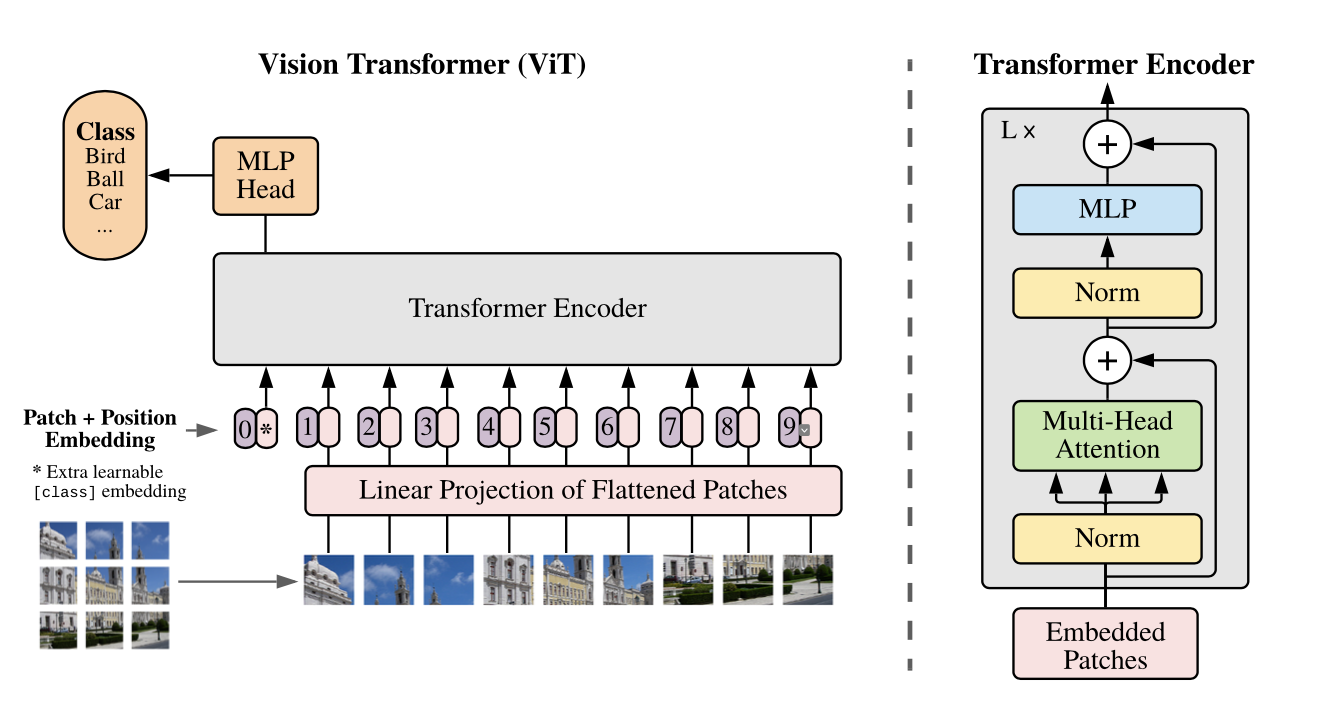
ViT는 기존 Transformer의 Encoder 구조를 사용한다. 따라서, Transformer에 맞는 입력 값을 사용해야한다. 기존 Transformer에서는 시퀀스 데이터를 Embedding 하고, Positional Encoding을 추가해준다. Vision Transformer에서도 동일한 방식을 거친다.
1️⃣ 입력 형태 만들기
- Image Patch 만들기
- 이미지를 패치 단위로 쪼개고, 각 패치를 왼쪽 상단에서 오른쪽 하단의 순서로 나열하여 시퀀스 데이터처럼 만든다.
- Patch Embedding
- 각 패치를 flatten하여 벡터로 변환하고, 각 벡터에 Linear projection 연산을 거쳐 Embedding 작업을 한다.
- Class Token
- Patch embedding 결과에 클래스를 예측하는 클래스 토큰을 하나 추가한다.
- Position Embedding
- 클래스 토큰이 추가된 입력 값에 Positional Embedding을 더해주면 ViT의 입력이 완성된다.
2️⃣ Encoder & MLP
- 앞 과정을 거쳐 만들어진 입력을 Encoder에 입력하여, Layer stack의 개수만큼 L번 반복한다. 반복 후, 입력값과 동일한 크기의 출력값을 마지막에 얻을 수 있다.
- Transformer Encoder의 출력 또한 클래스 토큰과 벡터로 이루어져있다. 이 중 클래스 토큰만 사용하여 위 구조의 MLP Head를 구성하고, 이를 이용하여 MLP를 거치면 최종적으로 클래스를 분류할 수 있다.
🔎 각 과정을 더 자세히 보자!
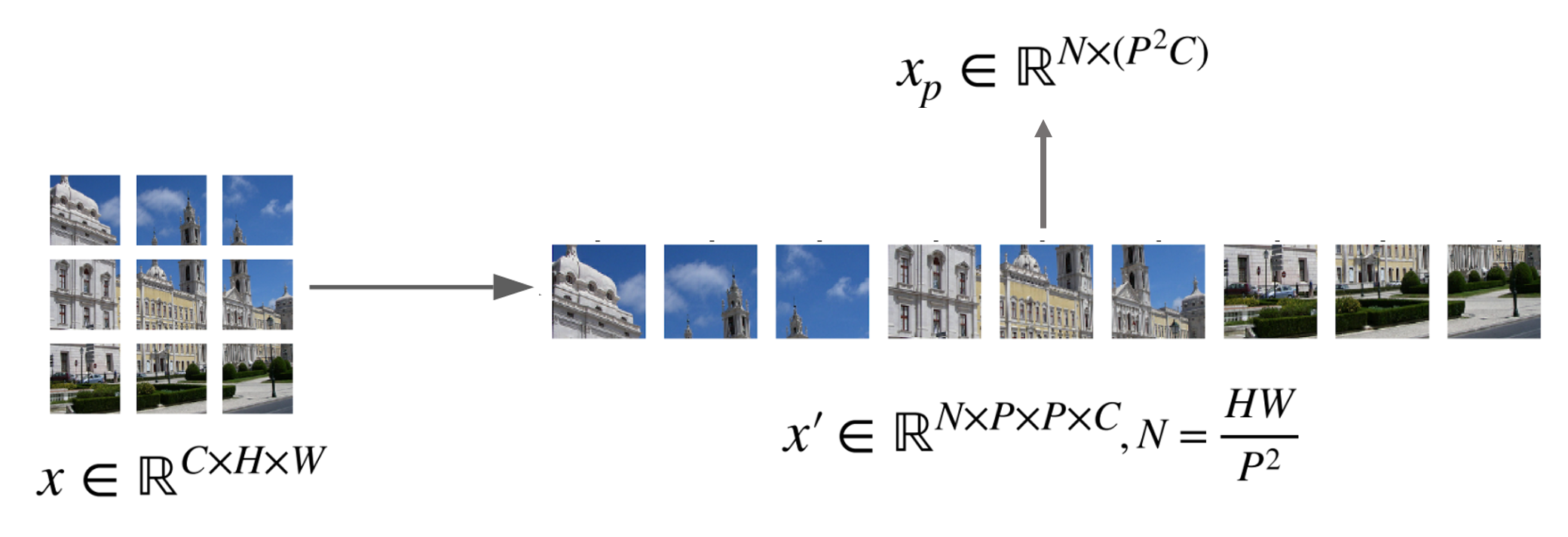
- 위 그림 기호 중 (C, H, W) 는 각각 Channel, Height, Width를 의미하며, P는 Patch의 크기, N은 나뉘어진 패치의 개수를 의미한다. 각 패치는 (C, P, P)의 크기를 가진다.
- 각 패치를 Flatten 과정을 거쳐 벡터로 만들면 각 벡터의 크기는 가 되고 이 벡터가 N개가 된다. 이 N개의 벡터를 합친 것을 라고 한다.
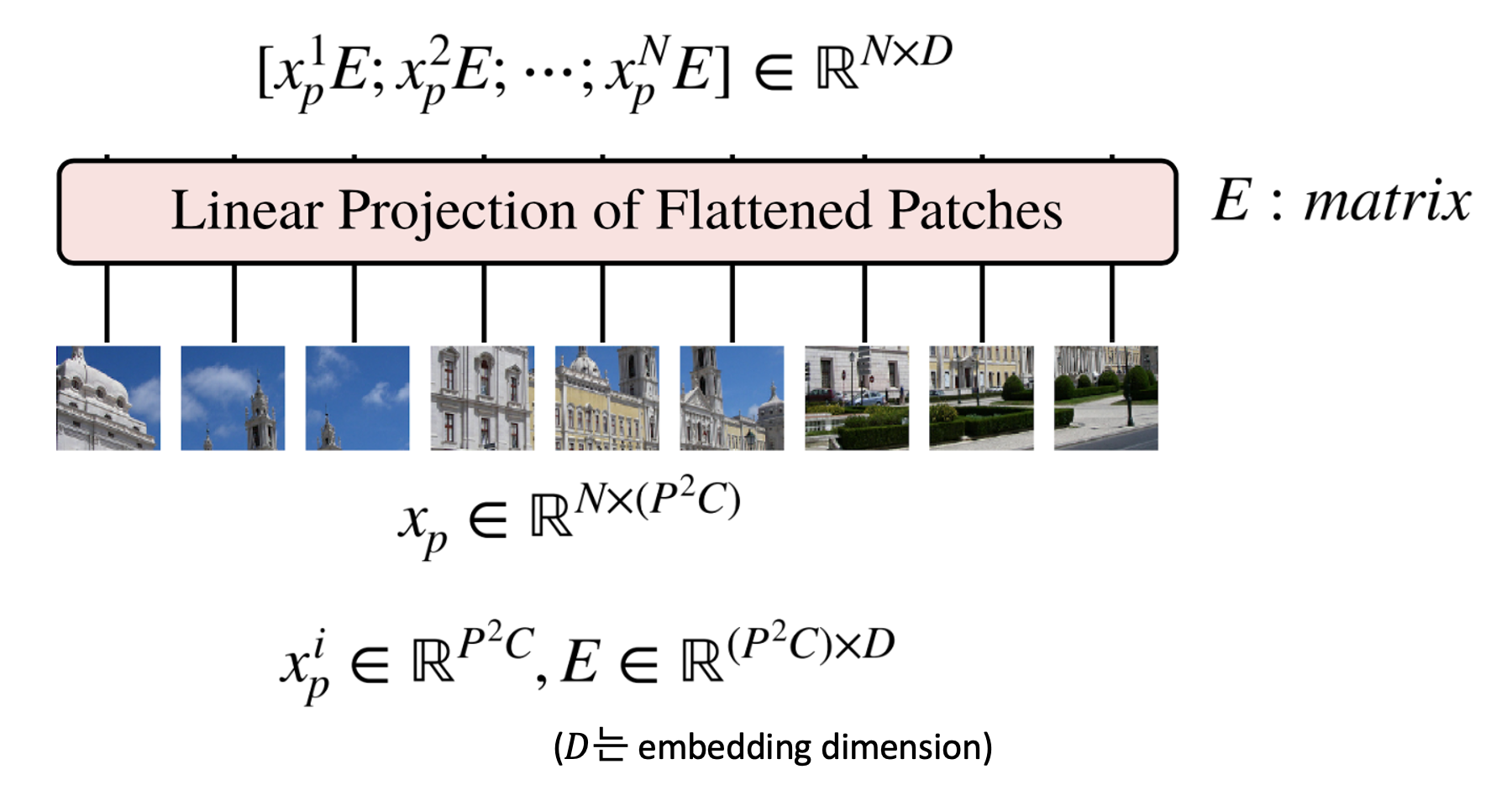
- 앞에서 생성한 를 Embedding 하기 위하여 행렬 와 연산을 한다. 의 shape은 () 가 된다. 는 embedding dimension으로 크기의 벡터를 로 변경하겠다는 의미이다.
- 따라서, 의 shape은 (), 의 shape은 ()으로 곱 연산을 하면 ()의 크기를 가지게 된다.
- 배치 사이즈까지 고려하면 ()의 크기를 가지는 텐서가 된다.

- Embedding한 결과에 클래스 토큰을 위 그림과 같이 추가한다. 그러면 (N, D) 크기의 행렬이 (N+1, D) 크기가 된다. 클래스 토큰은 학습 가능한 파라미터를 입력해 주어야 한다.
- 마지막으로 Positional Encoding을 추가하기 위하여 (N+1, D) 크기의 행렬을 더해주면 입력 값 준비가 마무리 된다.
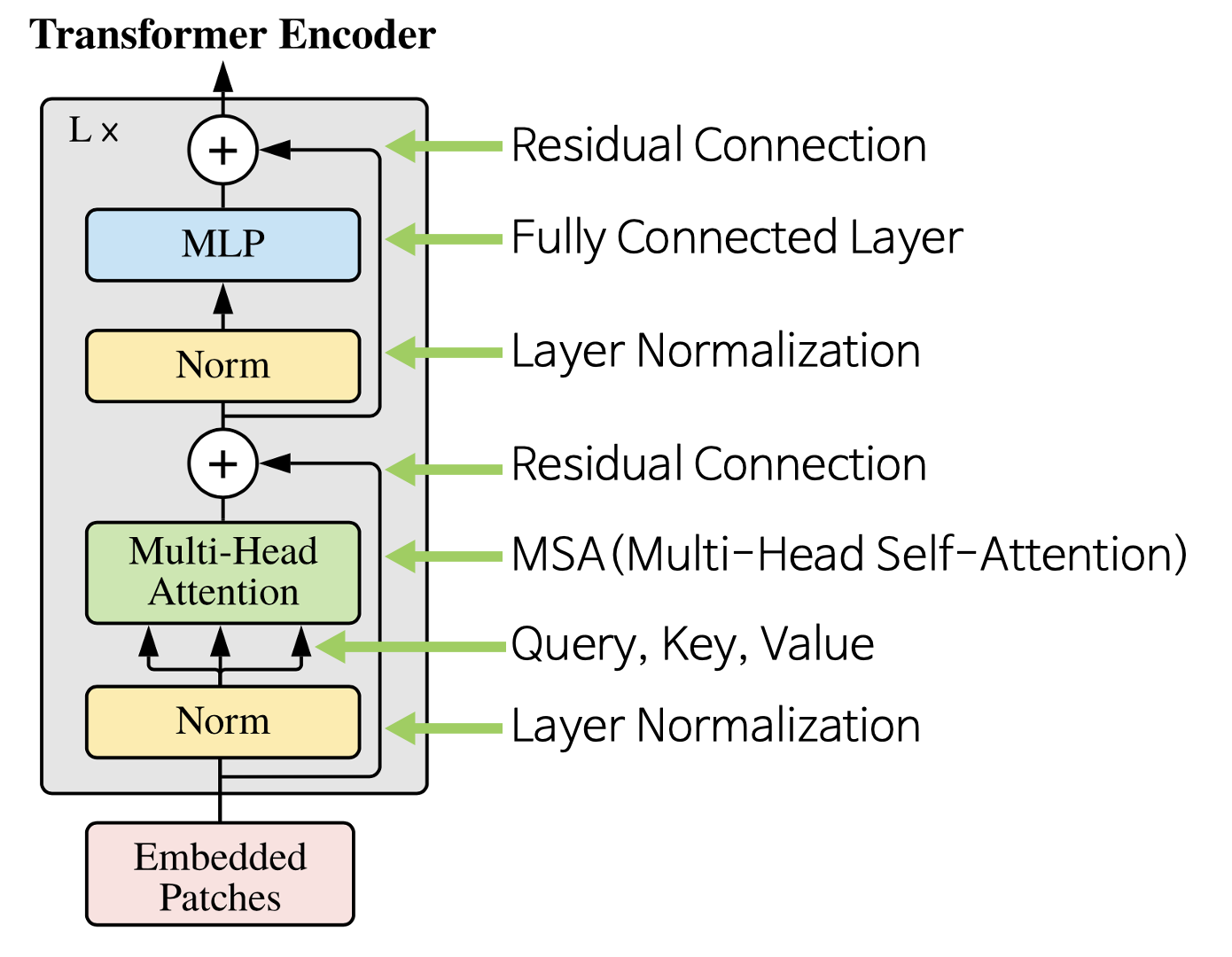
- Transformer의 Encoder는 번 반복하기 위해 입력과 출력의 크기가 같도록 유지한다.
- Vision Transformer에서 사용된 아키텍쳐는 기존의 Transformer Encoder와 조금 다르지만 큰 맥락은 유지한다. 기존의 Transformer Encoder에서는 MSA를 먼저 진행한 다음 LayerNorm을 진행하지만 ViT에서는 순서가 바뀌어 있는 것을 알 수 있다.
- 입력값 에서 시작하여 번 반복 시 이 최종 Encoder의 출력이 된다.
Multi-Head self-Attention
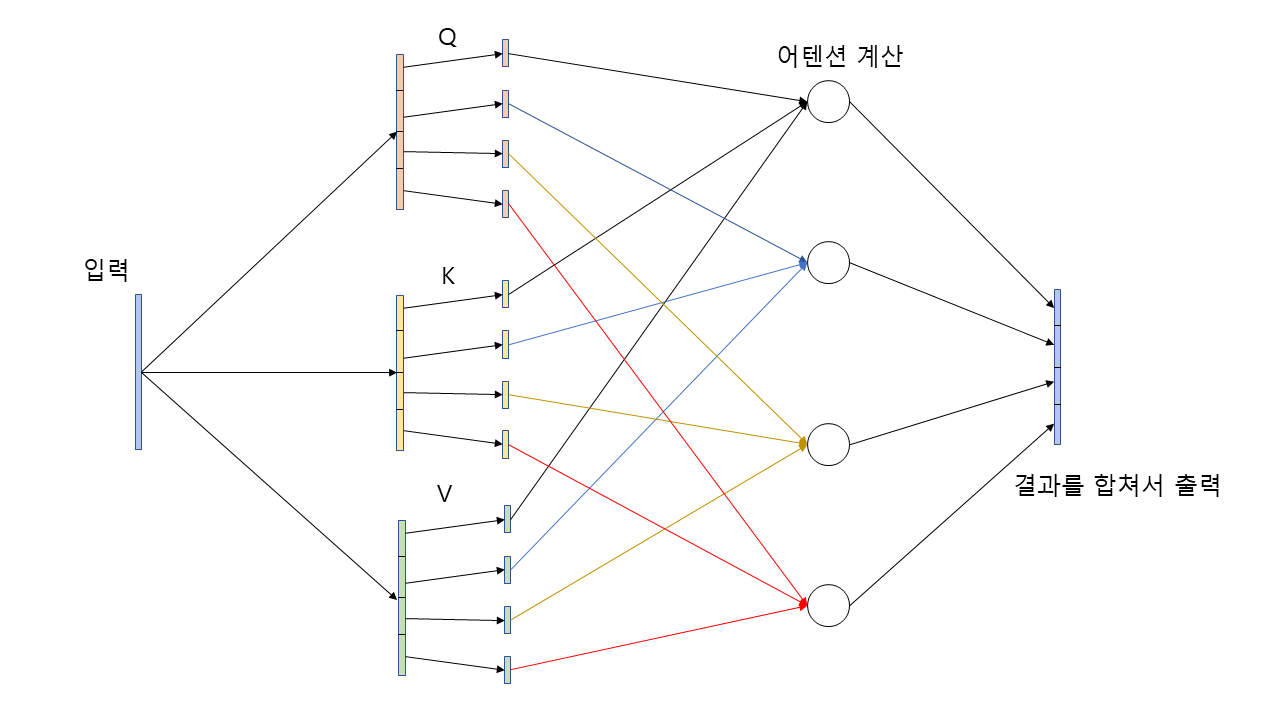
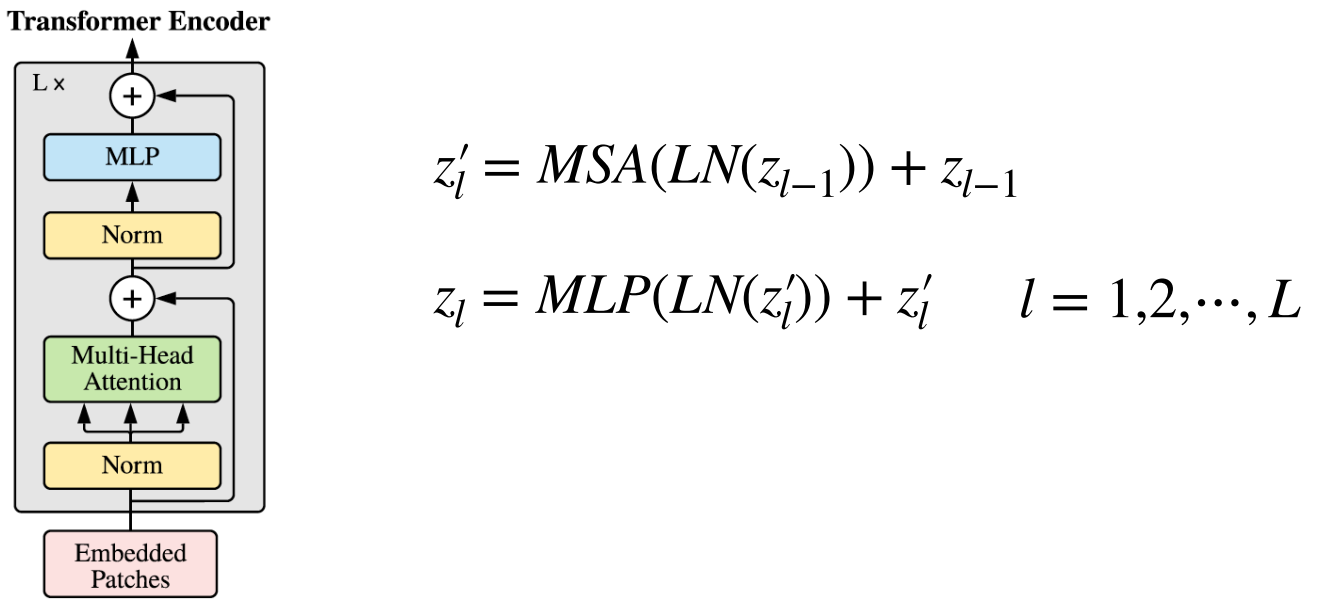
- 위 식과 같이 LayerNorm, MSA, MLP 연산을 조합하면 Transformer Encoder를 구현할 수 있다.
Layer Normalization
- Layer Normalization은 D차원에 대하여 각 feature에 대한 정규화를 진행한다.
- Transformer Encoder가 L번 반복할 때, 번째에서의 입력을 라고 하자.
- Layer Normalization은 D차원 방향으로 각 feature에 대하여 정규화를 진행하므로 다음 식을 따른다.
- 위 식에서 는 학습 가능한 파라미터이며, (3)식의 분모 변경은 분산이 0에 가까워졌을 때 처리하기 위한 트릭이다.
Multi-Head Self-Attention
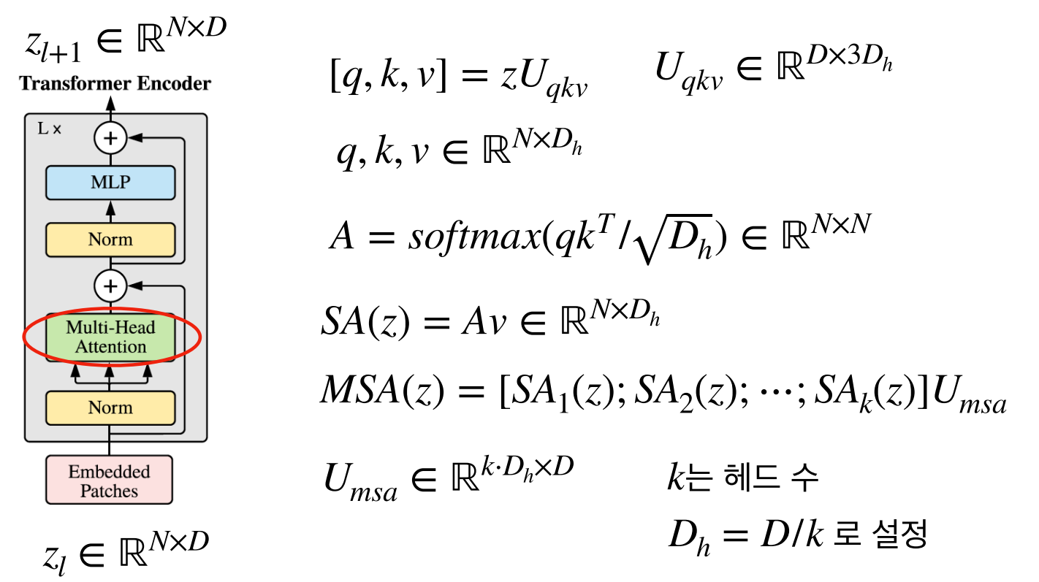
-
Notation의 표기를 간단히 하기 위하여 입출력을 로 사용하였다.
-
Attention 구조에 맞게 q(query), k(key), v(value)를 가지며, self-attention 구조에 맞게 다음 식과 같이 q, k, v가 구성된다.
-
q,k,v를 한번에 연산하기 위해서 (7) 식과 같이 사용하기도 한다.
-
식 (8), 식 (9)를 이용하여 각 head 에서의 self-attention 결과를 뽑고, 식 (10)을 이용하여 각 head의 self-attention 결과를 묶은 다음에 Linear 연산을 통해 최종적으로 Multi-Head Attention의 결과를 얻을 수 있다.
-
식 (10)에서 self-attention 결과를 묶은 것의 shape은 이고, 의 shape은 이므로 연산의 결과는 가 된다. 이 과정을 통해 Transformer Encoder의 입력과 같은 shape을 가지도록 조절할 수 있다.
-
실제 Multi-Head Attention을 구현할 때, 각 head의 에 대한 연산을 따로 하지 않고 한번에 처리할 수 있다.
-
위 식과 같이 같은 구조의 head에서 weight만 달라지게 되므로 다음과 같이 한번에 묶어서 연산할 수 있다.
MLP
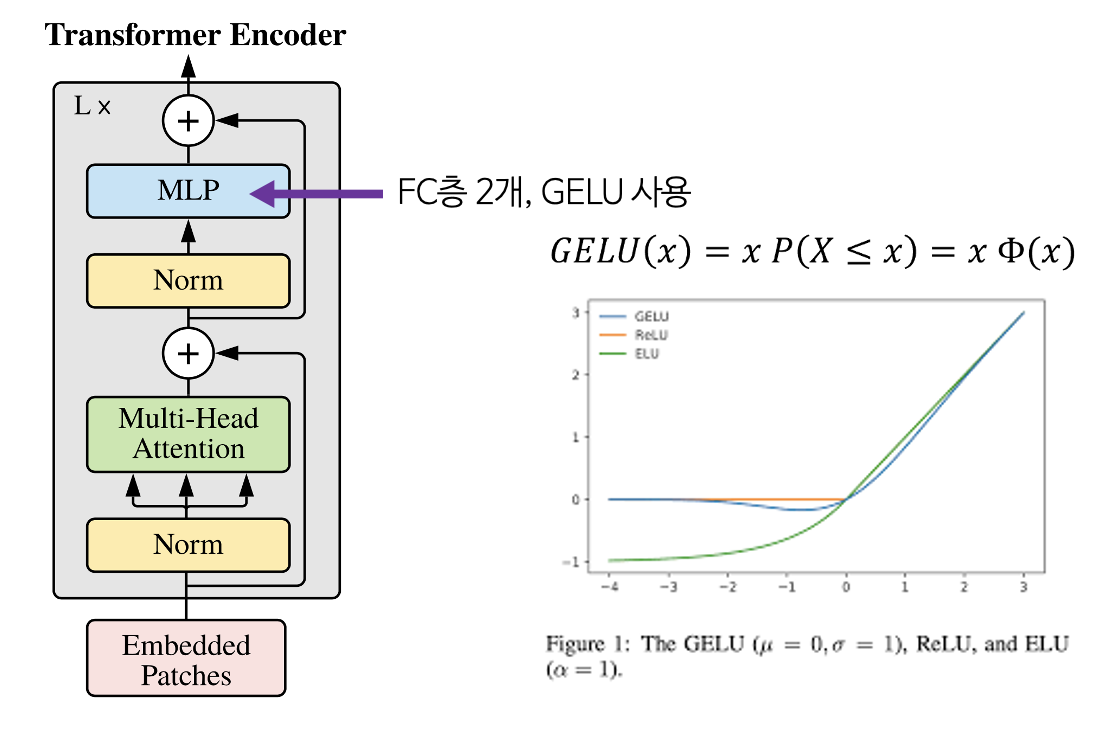
- 마지막으로 MLP 과정을 거치고 이때 GELU Activation을 사용한다.
- GELU는 입력값과 입력값의 누적정규분포의 곱을 사용한 형태이다. 이 함수 또한 모든 점에서 미분 가능하고 단조증가함수가 아니므로 Activation함수로 사용가능하며, 입력값 가 다른 입력에 비해 얼마나 큰 지에 대한 비율로 값이 조정되기 때문에 확률적인 해석이 가능해지는 장점이 있다.
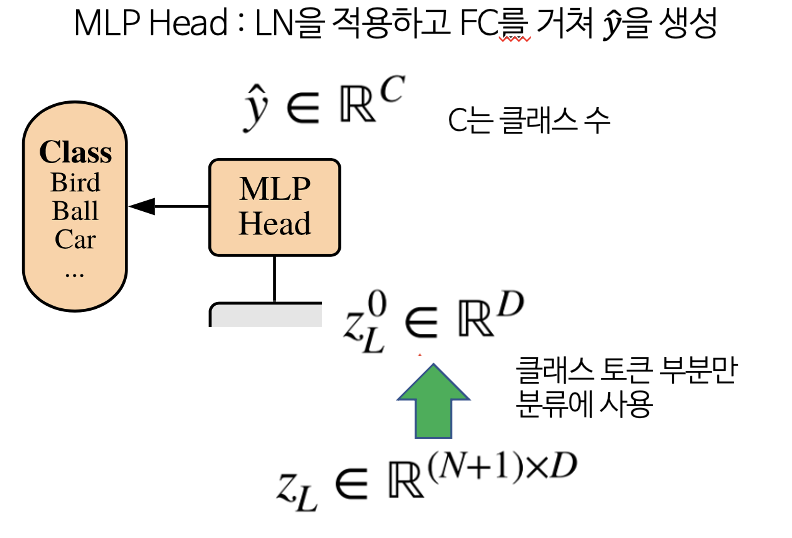
- L번 반복한 Transformer Encoder의 마지막 출력에서 클래스 토큰 부분만 분류 문제에 사용하며, 마지막에 추가적인 MLP를 이용하여 클래스를 분류한다.
참고자료
https://www.youtube.com/watch?v=hPb6A92LROc&t=493s
https://gaussian37.github.io/dl-concept-vit/
