수식으로 분해하는 선형 모델
- 신경망을 수식으로 분해하기 위해서는, 우선 선형 모델을 먼저 이해해야 함
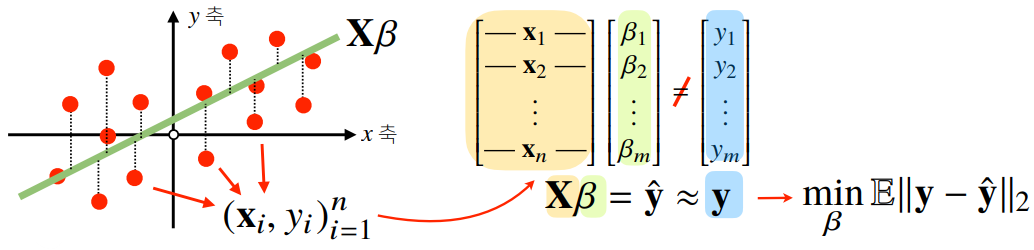
- 데이터 집합 을 통해,
- 를 만족하는,
- 선형식 을 세우기
수식으로 분해하는 비선형 모델(신경망)
- 비선형 모델인 신경망에서는, 각 행벡터 가 데이터 와 가중치 행렬 사이의 행렬곱과 절편 벡터의 합으로 표현된다고 가정
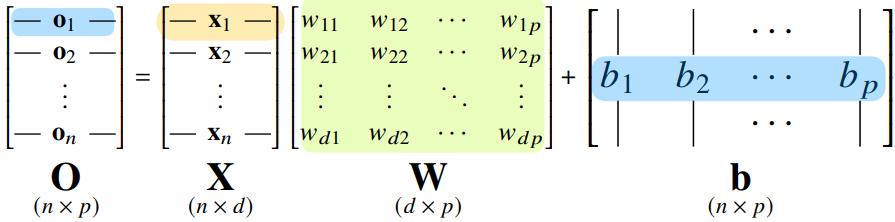
- 데이터가 바뀌면 결과값고 바뀌기 때문에, 출력 벡터의 차원이 에서 로 바뀌게 됨 → 개의 변수로 개의 선형 모델을 만들어 개의 잠재변수를 설명하는 모델로 생각할 수 있음
- 데이터가 바뀌면 결과값고 바뀌기 때문에, 출력 벡터의 차원이 에서 로 바뀌게 됨 → 개의 변수로 개의 선형 모델을 만들어 개의 잠재변수를 설명하는 모델로 생각할 수 있음
소프트맥스 연산
- 소프트맥스(softmax) 함수는 모델의 출력을 확률로 해석할 수 있게 변환
- 만약 출력 벡터 에 소프트맥스 함수를 적용하면 확률벡터가 되므로, 특정 클래스 에 속할 확률로 해석할 수 있음 → 분류 모델로 사용 가능
def softmax(vec): denumerator = np.exp(vec - np.max(vec, axis=-1, deepdims=True) numerator = np.sum(denumerator, axis=-1, keepdims=True) val = denumerator / numerator return val
활성화 함수
-
신경망은 선형 모델과 활성화 함수(activation function)을 합성한 함수
- 다시 말해, 활성화 함수가 없는 딥러닝은 선형 모델과 차이가 없음
-
활성화 함수 는 위에 정의된 비선형 함수로 잠재벡터 의 각 노드에 개별적으로 적용하여, 새로운 잠재벡터 를 만듬
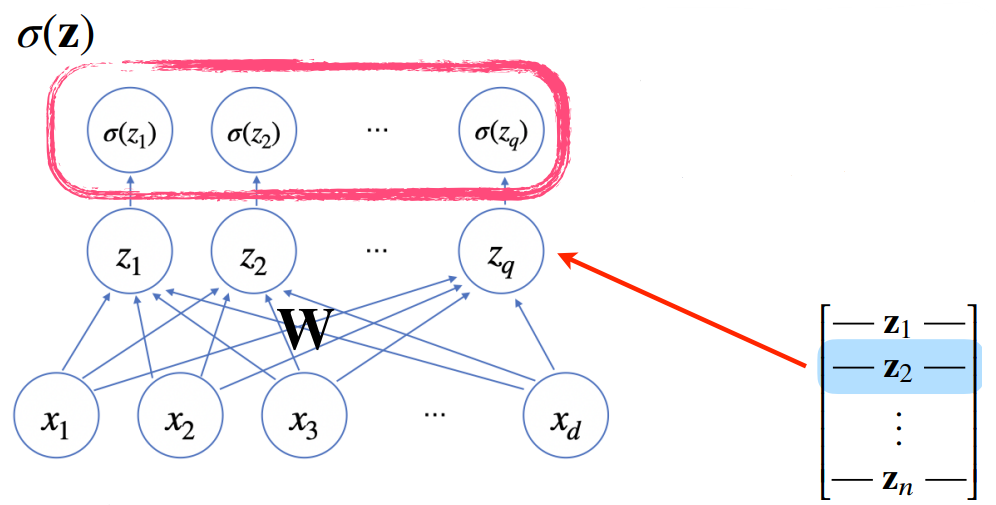
-
시그모이드(sigmoid) 함수나 tanh가 전통적으로 많이 쓰이던 활성화 함수이지만, 딥러닝에서는 ReLU(Rectified Linear Unit) 함수를 많이 사용함
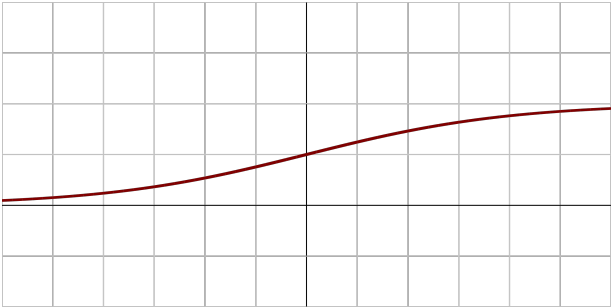
Sigmoid
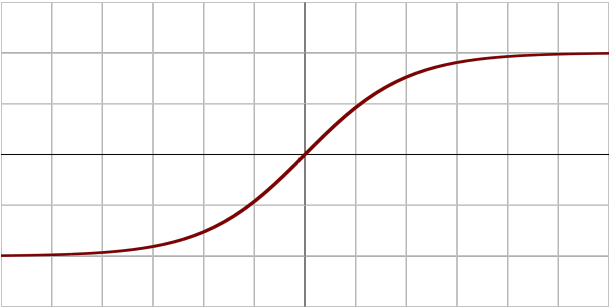
tanh
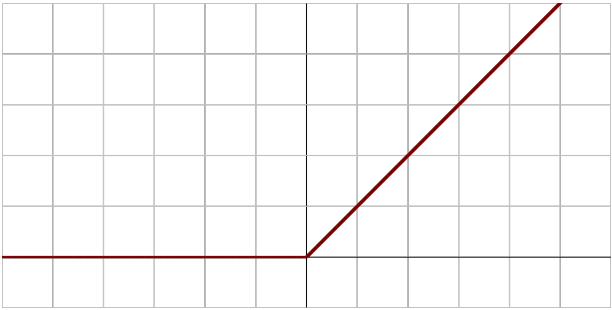
ReLU
-
-
잠재벡터 에서 가중치 행렬 와 를 통해 다시 한 번 선형변환해서 출력하게 되면, 을 매개변수로 가진 2층(2-layer) 신경망이 됨
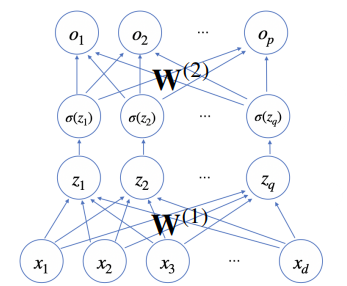
- 다층 퍼셉트론(multi-layer perceptron, MLP)은 신경망이 여러층 합성된 함수
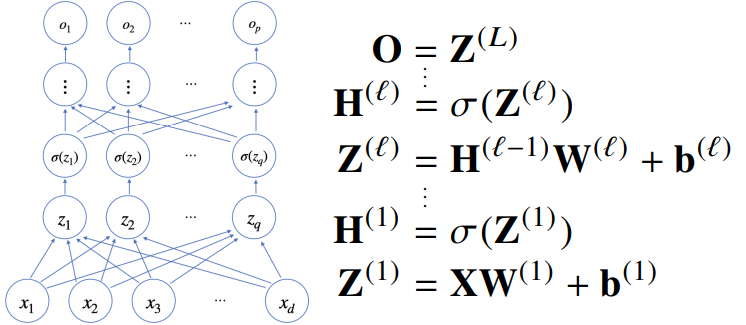
- MLP의 매개변수는 개의 가중치 행렬 로 구성됨
- 까지 순차적인 신경망 계산을 순전파(forward propagation)라고 함
- 다층 퍼셉트론(multi-layer perceptron, MLP)은 신경망이 여러층 합성된 함수
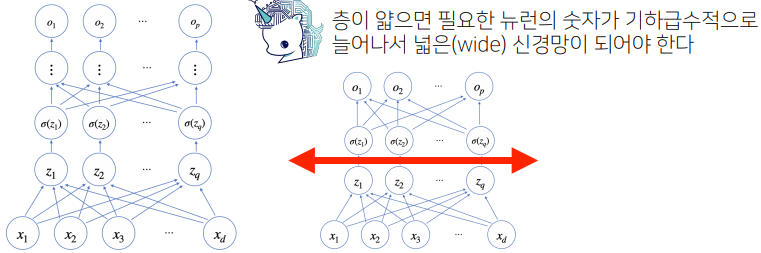
왜 ‘다층’인가?
- 이론적으로는 2층 신경망만으로도 임의의 연속함수를 근사할 수 있음
- 하지만 층이 깊을수록 목적함수를 근사하는데 필요한 노드의 숫자가 훨씬 빨리 감소하기 때문에, 더 효율적인 학습이 가능
역전파
- 딥러닝은 역전파(backpropagation) 알고리즘을 통해 각 층의 매개변수 를 학습
- 각 층 매개변수의 gradient 벡터 는 윗층부터 역순으로 계산하게 됨

- 역전파는 합성함수 미분법인 연쇄법칙(chain-rule) 기반 자동미분(auto-differentiation)을 사용
예제: 2층 신경망
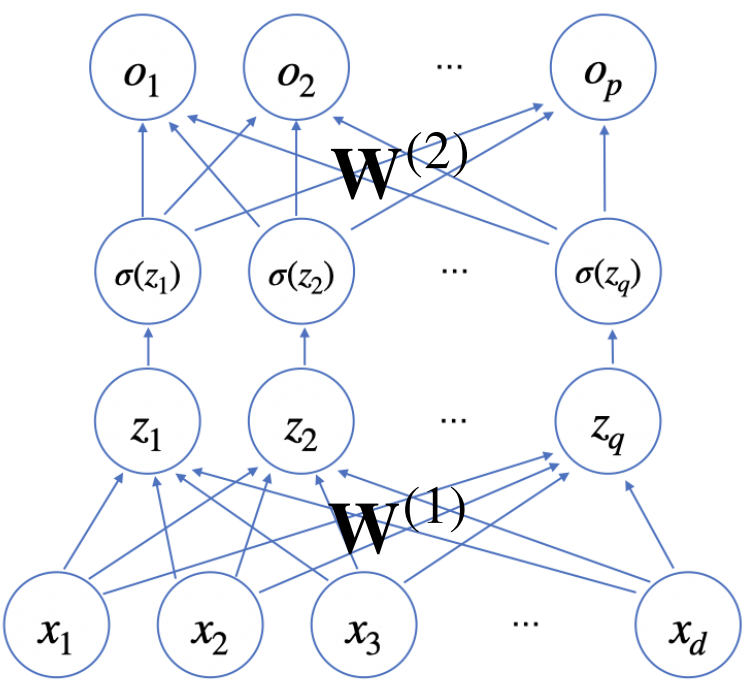
문제 상황:
- 은 행렬이므로, 각 성분에 대한 편미분을 구해야 함
