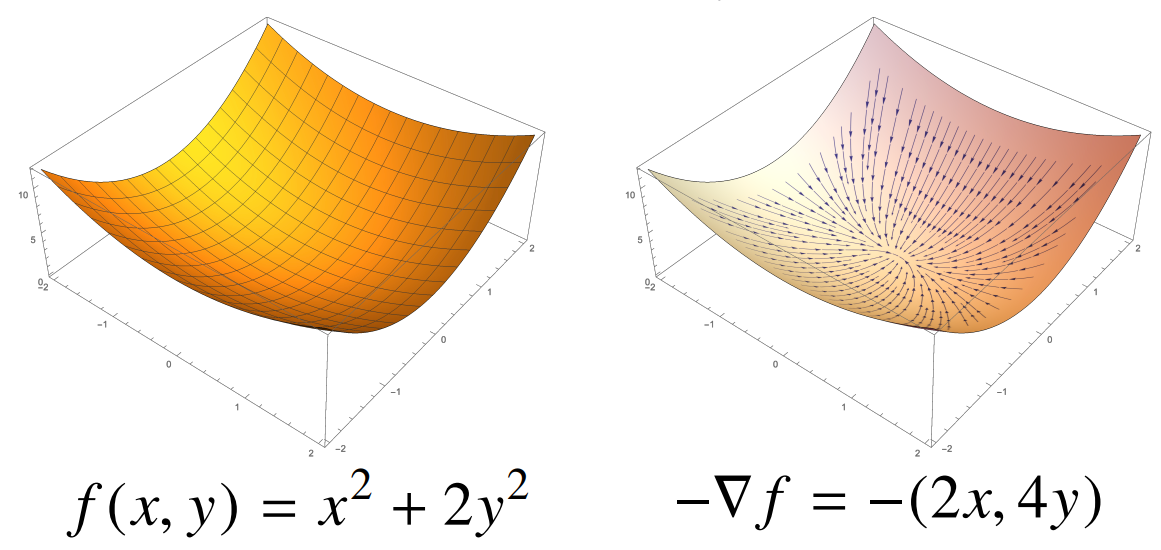미분이란

• 미분(differentiation)은 변수의 움직임에 따른 함수 값의 변화를 측정하기 위한 도구
  $f'(x)=\underset{h\rightarrow0}{\textrm{lim}}\frac{f(x+h)-f(x)}{h}$
  • 최적화에서 가장 많이 사용하는 기법
  • sympy라는 파이썬 라이브러리로 계산 가능

    import sympy
    from sympy.abc import x
    
    sym.diff(sym.poly(x**2 + 2*x + 3), x)
    # Poly(2*x + 2, x, domain='ZZ')

그림으로 이해하는 미분

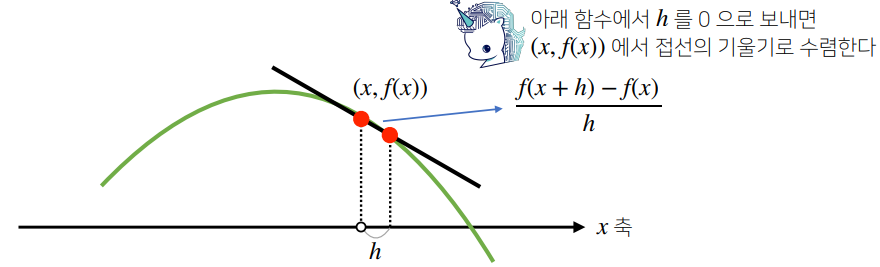
• 미분은 함수 $f$의 주어진 점 $(x,\,f(x))$에서 접선의 기울기를 구함
• 한 점에서 접선의 기울기를 알면, 어느 방향으로 점을 움직여야 함수값이 증가/감소하는지를 알 수 있음

경사하강법

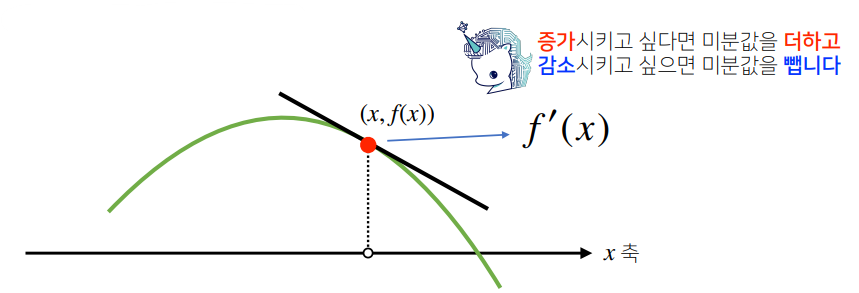
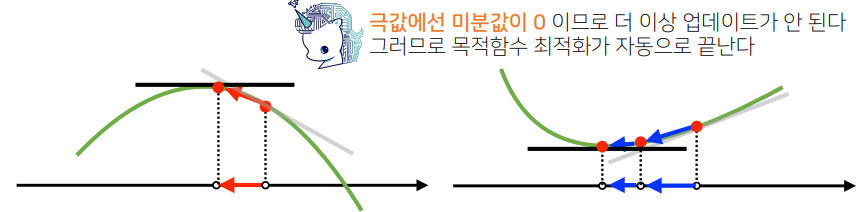
• 원래의 함수값에 미분값을 더하는/빼는 것을 경사상승법(gradient ascent)/경사하강법(gradient descent)라 하며, 함수의 극대/극소값 위치를 구할 때 사용
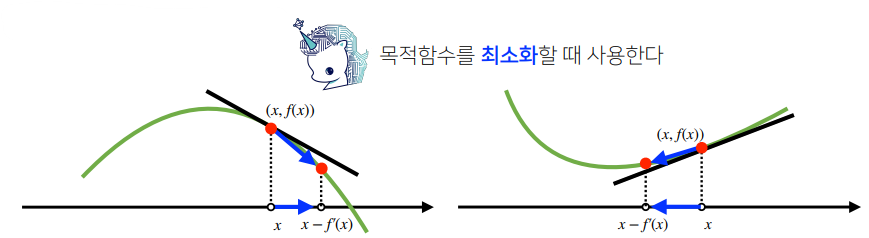
  • 두 방법 모두 극값에 도달하면 업데이트를 멈춤
    

코드로 보는 스칼라 경사하강법

Fortran

Input: gradient, init, lr, eps, Output: var

var = init
grad = gradient(var)
while(abs(grad) > eps):
	var = var - lr * grad
	grad = gradient(var)

• 수치해석을 통한 미분 시 미분값이 정확히 0이 되는 것은 불가능하므로 종료 기준인 eps를 설정
• var = var - lr * grad에서 업데이트($x-\lambda f'(x)$)를 진행하며, lr은 학습률 $\lambda$로 미분을 통한 업데이트 속도를 조절

Python

def func(val):
	fun = sym.poly(x**2 + 2*x + 3)
	return fun.subs(x, val), fun

def func_gradient(fun, val):
	_, function = fun(val)
	diff = sym.diff(function, x)
	return diff.subs(x, val), diff

def gradient_dexcent(fun, init_point, lr = 1e-2, epsilon=1e-5):
	cnt = 0
	val = init_point
	diff, _ = func_gradient(fun, init_point)
	while np.abs(diff) > epsilon:
		val = val - lr * diff
		diff, _ = func_gradient(fun, val)
		cnt += 1

	print("함수: {}, 연산횟수: {}, 최소점: ({}, {})".format(fun(val)[1], cnt, val, fun(val)[0]))

gradient_descent(fun=func, init_point=np.random.uniform(-2, 2))
# 함수: Poly(x**2 + 2*x + 3, x, domain='ZZ'), 연산횟수: 636, 최소점: (-0.999, 2.000)

변수가 벡터라면?: Gradient 벡터 $\nabla$

• 벡터가 입력인 다변수 함수의 경우 편미분(partial differentiation)을 사용
  $\partial_{x_i}f(\bold{x})=\underset{h\rightarrow0}{\textrm{lim}}\frac{f(\bold{x}+h\bold{e}_i)-f(\bold{x})}{h}$
  • 예시($x$ 편미분)
    $f(x,\,y)=x^2+2xy+3+cos(x+2y) \\ \rightarrow\partial_xf(x,\,y)=2x+2y-sin(x+2y)$

    import sympy as sym
    from sympy.abc import x, y
    
    sym.diff(sym.poly(x**2 + 2*x*y + 3) + sym.cos(x + 2*y)
    # 2*x + 2*y - sin(x + 2*y)

• 각 변수 별로 편미분을 계산한 gradient(기울기) 벡터를 이용하여 경사하강법에 사용
  $\nabla f=(\partial_{x_1}f,\partial_{x_2}f,\dots,\partial_{x_d}f)$
  • 미분값 $f'(x)$ 대신 벡터 $\nabla f$를 사용하여 변수 $\bold{x}=(x_1,\dots,x_d)$를 동시에 업데이트 가능
    
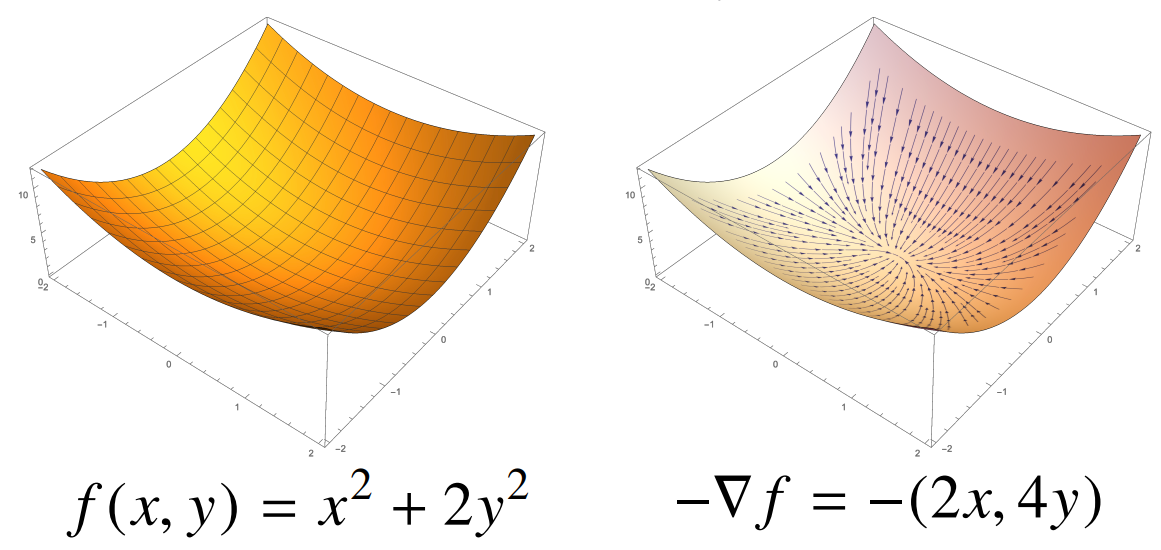
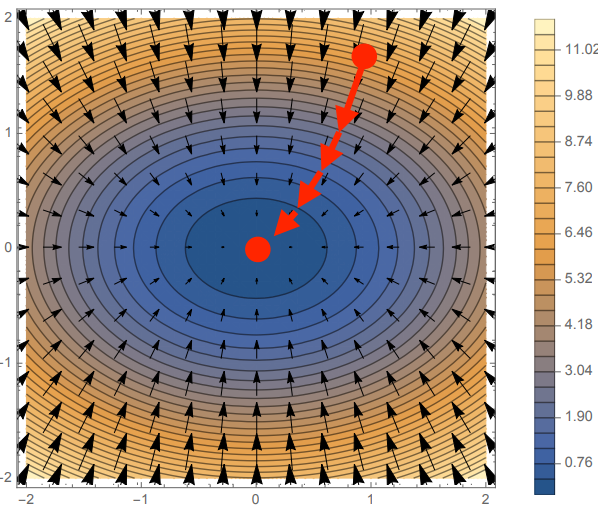
  • 이를 공간으로 표현하면, 각 점 $(x,\,y,\,z)$ 공간에서 $f(x,\,y)$ 표면을 따라
    $-\nabla f(=\nabla(-f))$벡터를 그릴 때 위와 같이 그릴 수 있음

코드로 보는 벡터 경사하강법

Fortran

Input: gradient, init, lr, eps, Output: var

var = init
grad = gradient(var)
while(abs(grad) > eps):
	var = var - lr * grad
	grad = gradient(var)

• 모두 동일하나, abs가 아닌 norm으로 계산하여 종료 조건 설정

Python

def eval_(fun, val):
	val_x, val_y = val
	fun_eval = fun.subs(x, val_x).subs(y, val_y)
	return fun_eval

def func_multi(val):
	x_, y_ = val
	func = sym.poly(x**2 + 2*y**2)
	return eval_(func, [x_, y_]), func

def func_gradient(fun, val):
	x_, y_ = val
	_, function = fun(val)
	diff_x = sym.diff(function, x)
	diff_y = sym.diff(function, y)
	grad_vec = np.array([eval_(diff_x, [x_, y_]), eval_(diff_y, [x_, y_])], dtype=float)
	return grad_vec, [diff_x, diff_y]

def gradient_descent(fun, init_point, lr=1e-2, epsilon=1e-5):
	cnt = 0
	val = init_point
	diff, _ = func_gradient(fun, val)
	while np.linalg.norm(diff) > epsilon:
		val = val - lr * diff
		diff, _ = func_gradient(fun, val)
		cnt += 1

	print("함수: {}, 연산횟수: {}, 최소점: ({}, {})".format(fun(val[1], cnt, val, fun(val)[0]))

pt = [np.random.uniform(-2, 2), np.random.uniform(-2, 2)]
gradient_descent(fun=func_multi, init_point=pt)

# 함수: Poly(x**2 + 2*y**2, x, y, domain='ZZ'), 연산횟수: 606, 최소점: ([4.959e-06 2.886e-11], 2.459E-11)

경사하강법을 이용한 선형회귀 계수 추정

• np.linalg.pinv를 이용하면 데이터를 선형모델(linear model)로 해석하는 선형회귀식을 찾을 수 있음
  • 원래의 식은 $\bold{X}\beta=\hat{\bold{y}}\approx{\bold{y}}\Rightarrow\beta=\bold{X}^{+}\bold{y}=(\bold{X}^T\bold{X})^{-1}\bold{X}^T\bold{y}$
  • 역행렬 대신 경사하강법으로 선형모델을 찾는다면?
• 선형회귀의 목적함수는 $\left\|\bold{y}-\bold{X}\beta\right\|_2$이고, 이를 최소화하는 $\beta$를 찾는 것
  • 다음과 같은 gradient vector를 구해야 함
    $\nabla_\beta\left\|\bold{y}-\bold{X}\beta\right\|_2 = (\partial_{\beta_1}\left\|\bold{y}-\bold{X}\beta\right\|_2,\dots,\partial_{\beta_d}\left\|\bold{y}-\bold{X}\beta\right\|_2)$
    • $\left\|\bold{y}-\bold{X}\beta\right\|_2$가 아닌 $\left\|\bold{y}-\bold{X}\beta\right\|_2^2$를 최소화해도 됨
  • 여기서,
    $\partial_{\beta_k}\left\|\bold{y}-\bold{X}\beta\right\|_2 = \displaystyle\partial_{\beta_k}\{\frac{1}{n}\sum^n_{i=1}(y_i-\sum^d_{j=1}X_{ij}\beta_j)^2\}^{1/2} = -\frac{\bold{X}^T_{\cdot k}(\bold{y}-\bold{X}\beta)}{n\left\|\bold{y}-\bold{X}\beta\right\|_2}$
    이므로,
    • $\bold{X}^T_{\cdot k}$: 행렬 $\bold{X}$의 $k$번째 열벡터를 전치(transpose)시킨 것
  • 그레디언트 벡터 $\nabla_\beta\left\|\bold{y}-\bold{X}\beta\right\|_2$은
    $\nabla_\beta\left\|\bold{y}-\bold{X}\beta\right\|_2 = (-\frac{\bold{X}^T_{\cdot 1}(\bold{y}-\bold{X}\beta)}{n\left\|\bold{y}-\bold{X}\beta\right\|_2} ,\dots, -\frac{\bold{X}^T_{\cdot d}(\bold{y}-\bold{X}\beta)}{n\left\|\bold{y}-\bold{X}\beta\right\|_2}) \\= -\frac{\bold{X}^T(\bold{y}-\bold{X}\beta)}{n\left\|\bold{y}-\bold{X}\beta\right\|_2}$
    가 됨
    • 즉, 계산이 복잡해도 사실 $\bold{X}\beta$를 계수 $\beta$에 대해 미분한 결과에 $\bold{X}^T$만 곱하는 것
• 결과적으로, 목적함수를 최소화하는 $\beta$를 구하는 경사하강 알고리즘은 다음과 같음
  $\beta^{(t+1)} \leftarrow \beta^{(t)}-\lambda\nabla_\beta\left\|\bold{y}-\bold{X}\beta^{(t)}\right\| = \beta^{(t)}+\frac{\lambda}{n}\frac{\bold{X}^T(\bold{y}-\bold{X}\beta^{(t)})}{\left\|\bold{y}-\bold{X}\beta^{(t)}\right\|}$
  • $\left\|\bold{y}-\bold{X}\beta\right\|_2$ 대신 $\left\|\bold{y}-\bold{X}\beta\right\|_2^2$를 목적함수로 가정하는 경우 식이 더 간단해짐
    $\beta^{(t+1)} \leftarrow \beta^{(t)}+\frac{2\lambda}{n}\bold{X}^T(\bold{y}-\bold{X}\beta^{(t)})$

코드 구현

import numpy as np

X = np.array([[1, 1], [1, 2], [2, 2], [2, 3]])
y = np.dot(X, np.array([1, 2])) * 3

beta_gd = [10.1, 15.1, -6.5] # [1, 2, 3]이 정답임
X_ = np.array([np.append(x, [1]) for x in X]) # intercept 항 추가

for t in range(5000):
    error = y - X_ @ beta_gd
    # error = error / np.linalg.norm(error)
    grad = -np.transpose(X_) @ error
    beta_gd = beta_gd - 0.01 * grad

print(beta_gd)

확률적 경사하강법 (Stochastic Gradient Descent, SGD)

• 이론적으로, 경사하강법은 (1) 미분 가능하고 (2) 볼록(convex)한 함수에 대해 (3) 적절한 학습률과 학습 횟수를 선택했을 때만 수렴이 보장됨
  • 선형회귀의 경우 목적식 $\left\|\bold{y}-\bold{X}\beta\right\|_2$은 회귀계수 $\beta$에 대해 볼록함수 → 수렴 보장
  • 하지만, 비선형회귀의 경우 목적식이 볼록하지 않을 수 있음 → 수렴 보장 안됨
    
• SGD는 모든 데이터를 사용해 업데이트하는 대신, 데이터 한 개 또는 일부를 활용하여 업데이트
  • 볼록이 아닌(non-convex) 목적함수는 SGD를 통해 최적화할 수 있음
    $\theta^{(t+1)}\leftarrow\theta^{(t)}-\widehat{\nabla_\theta\mathcal{L}}(\theta^{(t)})\quad(\because\mathbb{E}[\widehat{\nabla_\theta\mathcal{L}}]\approx\nabla_\theta\mathcal{L})$
  • SGD가 만능은 아니지만, 딥러닝 학습의 경우 일반 경사하강법보다 일반적으로 더 낫다고 검증됨
• 데이터의 일부를 이용해 매개변수를 업데이트하기 때문에, 연산자원을 더 효율적으로 활용하는데 도움이 됨
  • 전체 데이터($\bold{X}$, $\bold{y}$)를 사용하지 않고, 미니배치($\bold{X}_{(b)}$, $\bold{y}_{(b)}$)를 사용하므로 연산량이 $b/n$으로 감소

미니배치 연산

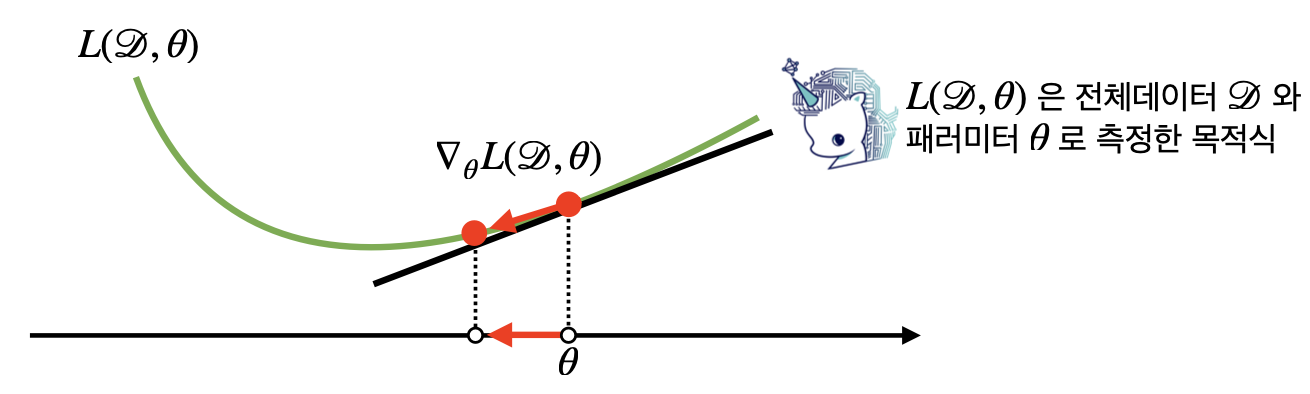
• 경사하강법은 전체 데이터 $\mathscr{D}=(\bold{X},\bold{y})$를 가지고 목적함수의 그래디언트 벡터 $\nabla_\theta L(\mathscr{D},\theta)$를 계산
  
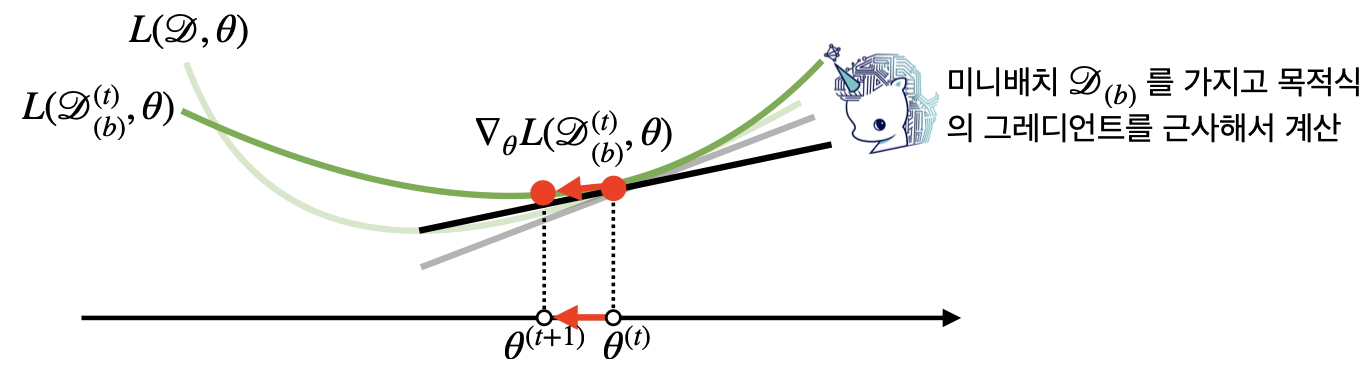
• SGD의 경우 미니배치 $\mathscr{D}_{(b)}=(\bold{X}_{(b)},\bold{y}_{(b)})\subset\mathscr{D}$를 가지고 그래디언트 벡터를 계산
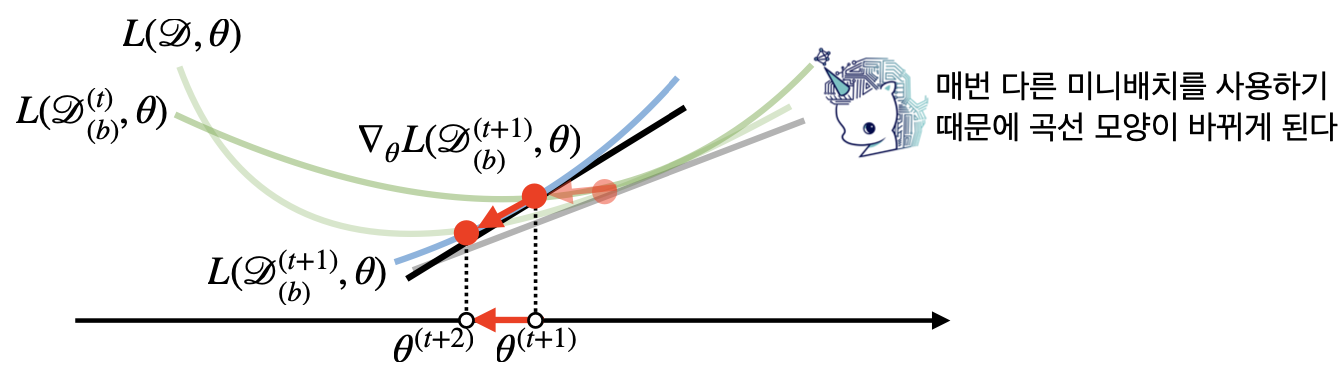
  • 미니배치는 확률적으로 임의 선택되기 때문에 목적 함수 모양이 매번 바뀌게 됨
    
  • 볼록이 아닌 목적식에서도 사용이 가능하기 때문에, 일반 경사하강법보다 ML/DL 학습에 효율적

하드웨어 상의 SGD

• 오늘날 모델 학습 데이터는 매우 방대함
  • 예를 들어, 256 ⨉ 256 ⨉ 3의 이미지 데이터가 100만 장 존재하는 경우, 그 크기가 약
    $256\times256\times3\times1,000,000\approx2^{37}\;\textrm{bytes}$
  • 일반 경사하강법처럼 모든 데이터를 업로드하면 메모리가 부족함
• 미니배치로 쪼개서 업로드하는 경우
  $256\times256\times3\times|\mathscr{B}|\leq2^{18}\cdot|\mathscr{B}|\;\textrm{bytes}$
  로 줄어듬
  • GPU에서 행렬 연산과 모델 매개변수를 업데이트
  • CPU는 전처리와 GPU에 업로드할 데이터 준비