벡터란

• 벡터(vector): 숫자를 원소로 가지는 리스트(list) 또는 배열(array)
  
• 공간에서의 한 점을 나타냄
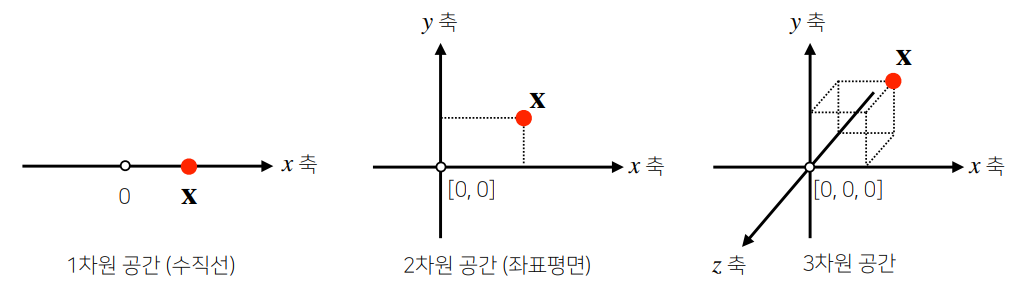
  • 원점으로부터 해당 점의 상대적 위치를 표현
  • 숫자(스칼라)를 곱해주면 방향은 그대로, 길이만 변함 → $\alpha\bold{x}=[\alpha x_1\quad\alpha x_2\quad...\quad\alpha x_d]$
    

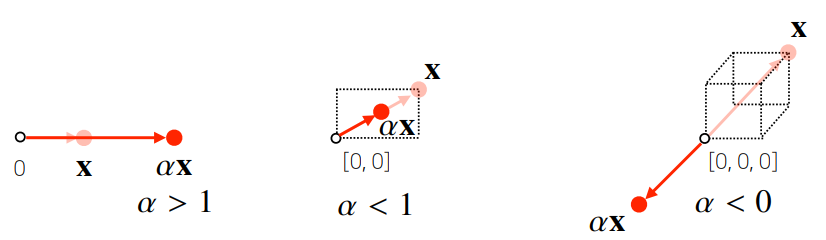
벡터의 연산

기본 사칙 연산

• 다수의 벡터 간에 같은 모양을 가지는 경우 덧셈, 뺄셈, 성분곱(Hadamard product) 등의 기본 사칙 연산 가능
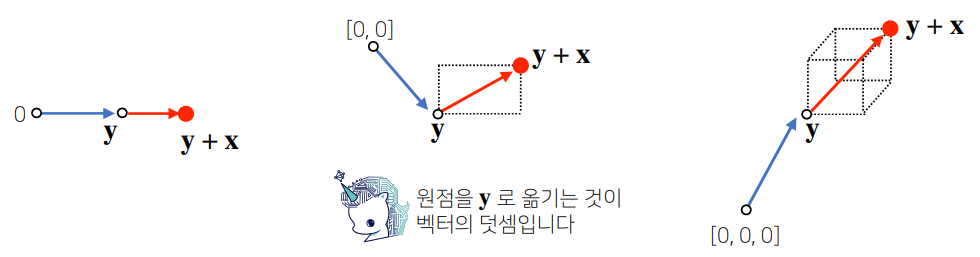
  • 두 벡터의 덧셈은 다른 벡터로부터의 상대적 위치이동을 표현
    

노름(norm)

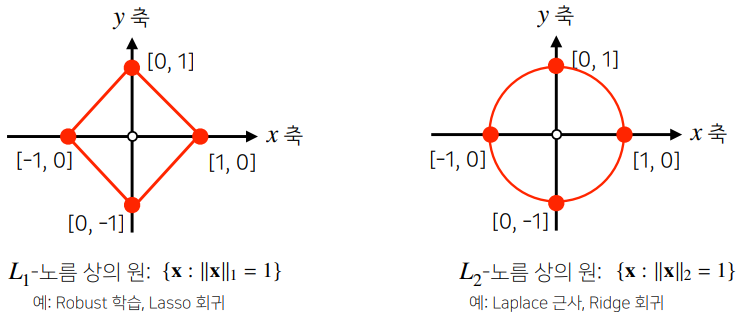
• 노름(norm, ∥)은 원점에서부터의 거리를 뜻함
  • $L_1$-norm은 각 성분의 변화량 절대값을 단순히 더하는 것 → $\parallel\bold{x}\parallel_1=\displaystyle\sum^d_{i=1}|x_i|$
  • $L_2$-norm은 피타고라스 정리 기반 유클리드 거리 → $\parallel\bold{x}\parallel_2=\displaystyle\sqrt{\sum^d_{i=1}|x_i|^2}$
  • 노름의 종류에 따라 기하학적 성질이 달라지며, ML에서는 두 성질 모두 사용하는 때가 있음
    

두 벡터를 이용한 연산

두 벡터 간 거리

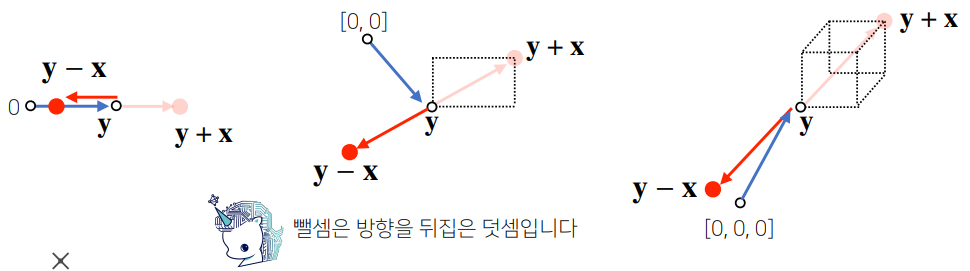
• 두 벡터 사이 거리 계산에는 벡터의 뺄셈과 $L_2$-norm 사용
  • $\parallel\bold{y}-\bold{x}\parallel_2 \;=\;\parallel\bold{x}-\bold{y}\parallel_2$
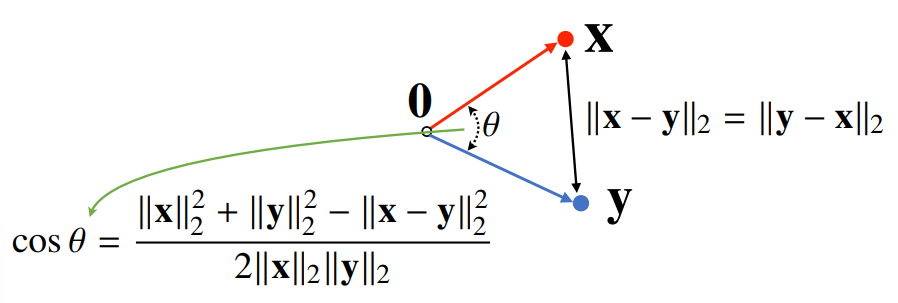
  • 뺄셈을 거꾸로 해도 거리는 같음

두 벡터 간 각도

• 두 벡터 사이 각도 계산에는 제2코사인 법칙과 내적을 이용
  $cos\,\theta=\displaystyle\frac{\parallel\bold{x}\parallel^2_2+\parallel\bold{y}\parallel^2_2-\parallel\bold{x}-\bold{y}\parallel^2_2}{2\parallel\bold{x}\parallel_2\parallel\bold{y}\parallel_2}=\frac{2<\bold{x},\;\bold{y}>}{2\parallel\bold{x}\parallel_2\parallel\bold{y}\parallel_2}=\frac{\displaystyle\sum^d_{i=1}x_iy_i}{\parallel\bold{x}\parallel_2\parallel\bold{y}\parallel_2}$
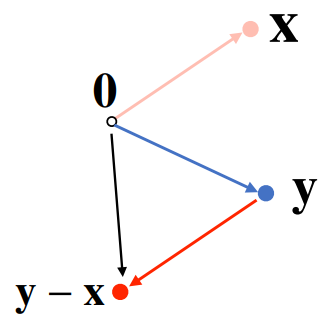
  • $\displaystyle\sum^d_{i=1}x_iy_i$: 벡터의 내적

내적(Inner product, Dot product)

• 내적은 정사영(orthogonal projection)된 벡터의 길이와 관련이 있음

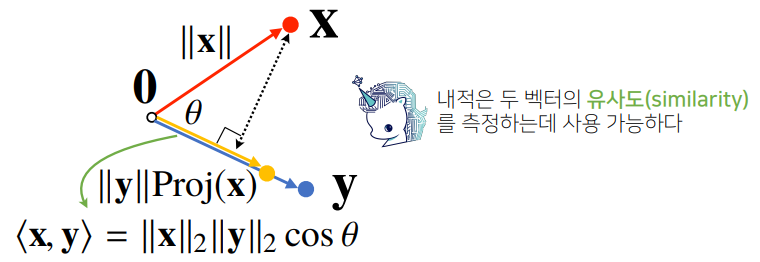
  • $proj(\bold{x})$의 길이는 코사인법칙에 의해 $\parallel\bold{x}\parallel cos\,\theta$가 됨

  • 내적은 정사영의 길이를 벡터 $\bold{y}$의 길이 $\parallel\bold{y}\parallel$만큼 조정한 값

    ⇒ $<\bold{x},\;\bold{y}>=\parallel\bold{x}\parallel_2\parallel\bold{y}\parallel_2cos\,\theta

행렬이란

• 행렬(matrix)은 벡터를 원소로 가지는 2차원 배열
  • 행(rwo)과 열(column)이라는 인덱스를 가짐
  • 행렬의 특정 행(또는 열)을 고정하면 행(또는 열)벡터라고 부름
  • 행과 열의 인덱스를 바꾼 행렬을 전치(transpose) 행렬이라고 함
    
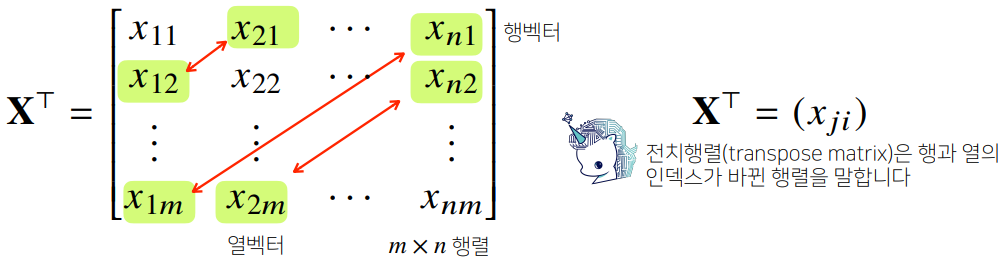
• 벡터는 공간에서의 한 점을 의미 → 행렬은 벡터의 집합, 즉 공간에서의 여러 점들을 의미
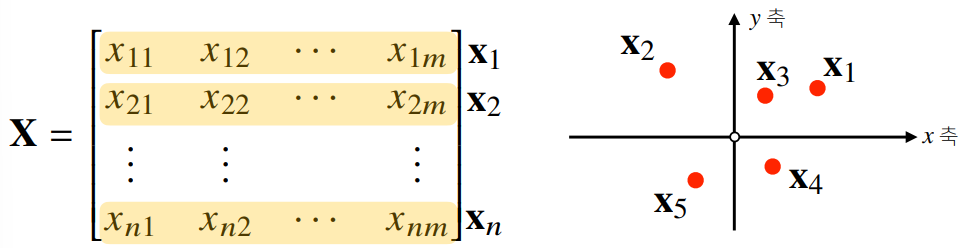
  • 행렬의 행벡터 $\bold{x}_i$는 $i$ 번째 데이터를 의미
  • 행렬의 $x_{ij}$는 $i$ 번째 데이터의 $j$ 번째 변수의 값을 뜻함
    

행렬의 연산

기본 연산

• 행렬끼리 같은 모양을 가지는 경우, 덧셈, 뺄셈, 성분곱, 스칼라곱 등 기본 연산이 가능
  $\bold{X}\;\pm\;\bold{Y}=\sum(x_{ij}\;\pm\;y_{ij}) \\ \bold{X}\;\odot\;\bold{Y}=\sum(x_{ij}\;\odot\;y_{ij}) \\ \alpha\bold{X}=\begin{bmatrix} \alpha x_{11} & \alpha x_{12} & \dots & \alpha x_{1m} \\ \alpha x_{21} & \alpha x_{22} & \dots & \alpha x_{2m} \\ \vdots & \vdots & & \vdots \\ \alpha x_{n1} & \alpha x_{n2} & \dots & \alpha x_{nm} \\ \end{bmatrix}$

행렬 간 곱셈

• 행렬 곱셈(matrix multiplication)은 $i$ 번째 행벡터와 $j$ 번째 열벡터 사이 내적을 성분으로해

  X = np.array([[1, -2, 3], [7, 5, 0], [-2, -1, 2]]) # 3 × 3 크기
  Y = np.array([[0, 1], [1, -1], [-2, 1]]) # 3 × 2 크기
  
  X @ Y # numpy에서는 @ 연산으로 행렬 곱셈을 나타냄
  # array([[-8, 6], [5, 2], [-5, 1]])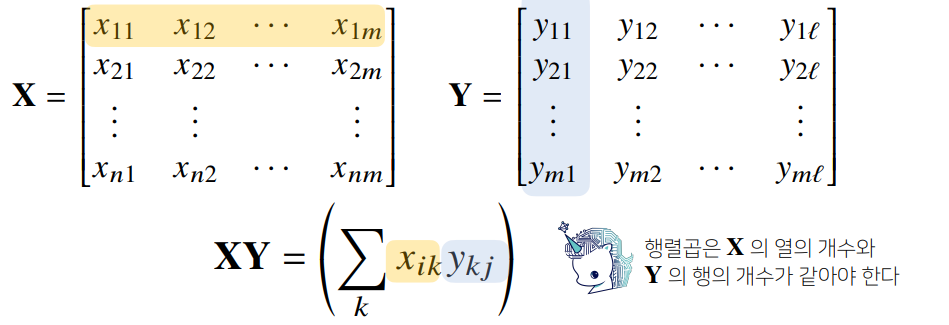

  
  • $(i\times k)\times(k\times j)=(i\times j)$

행렬 간 내적

• np.inner는 $i$ 번째 행벡터와 $j$ 번째 행 벡터 사이 내적을 성분으로 가지는 행렬을 계산함

  X = np.array([[1, -2, 3], [7, 5, 0], [-2, -1, 2]]) # 3 × 3 크기
  Y = np.array([[0, 1, -1], [1, -1, 0]]) # 2 × 3 크기
  
  np.inner(X, Y)
  # array([[-5, 3], [5, 2], [-3, -1]]) # 3 × 2 크기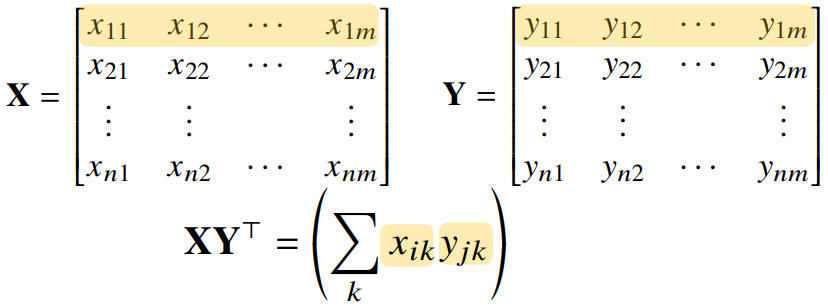

  
  • 수학에서 말하는 내적과는 다소 다름
  • $(i\times k)\times(j\times k)=(i\times j)$해

연산자(Operator)로써의 행렬

• 행렬은 벡터 공간에서 사용되는 연산자(operator)로 이해할 수 있음
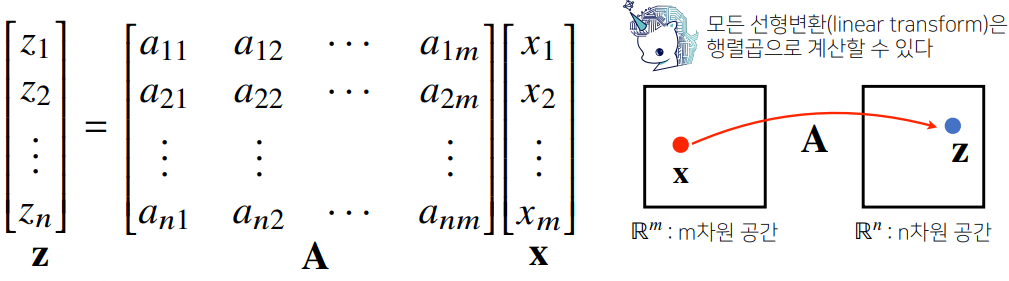
  • 행렬곱을 통해 벡터를 다른 차원의 공간으로 보내거나
  • 패턴을 추출할 수도 있고, 데이터를 압축할 수도 있음

역행렬

• 어떤 행렬 $\bold{A}$의 연산을 거꾸로 되돌리는 행렬을 역행렬(inverse matrix)라고 하며, $\bold{A}^{-1}$로 표기
  $\bold{AA}^{-1}=\bold{A}^{-1}\bold{A}=\bold{I}$
  • Numpy에서는 np.linalg.inv(X)로 사용 가능
  • 역행렬은 행과 열 크기가 같은 정사각행렬이면서, 행렬식(determinant)가 0이 아닌 경우에만 계산할 수 있음
• 역행렬을 계산할 수 없는 행렬이라면, 유사역행렬(pseudo-inverse) 또는 무어-펜로즈(Moore-Penrose) 역행렬인 $\bold{A}^+$를 이용
  $\bold{A}^+=(\bold{A}^T\bold{A})^{-1}\bold{A}^T\quad if\quad n\geq m \\ \bold{A}^+=\bold{A}^T(\bold{A}^T\bold{A})^{-1}\quad if\quad n\leq m$
  • Numpy에서는 np.linalg.pinv(X)로 사용 가능
  • 이를 이용하는 경우 연립 방정식의 해를 구할 수 있음
    $\bold{Ax}=\bold{b}\quad↔\quad\bold{x}=\bold{A}^+\bold{b}=\bold{A}^T(\bold{AA}^T)^{-1}\bold{b}$
  • $n\geq m$(데이터가 변수 개수보다 많거나 같은)인 경우, 데이터를 선형 모델로 해석하는 선형회귀식도 찾을 수 있음
    $\bold{X}\beta=\hat{\bold{y}}\approx\bold{y}\quad(\textrm{makes}\;\underset{\beta}{min}\parallel\bold{y}-\hat{\bold{y}}\parallel_2) \\ \beta=\bold{X}^+\bold{y}=(\bold{X}^T\bold{X})^{-1}\bold{X}^T\bold{y}$

    # Scikit-Learn-based Linear Regression
    from sklearn.linear_model import LinearRegression
    model = LinearRegression()
    model.fit(X, y)
    y_test = model.predict(x_test)
    
    # Moore-Pensore-Inverse-Matrix-based Linear Regression
    X_ = np.array([np.append(x, [1]) for x in X])
    beta = np.linalg.pinv(X_) @ y
    y_test = np.append(x, [1]) @ beta