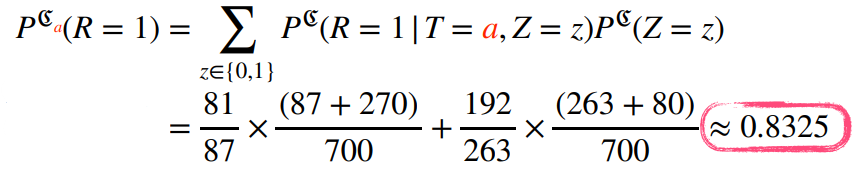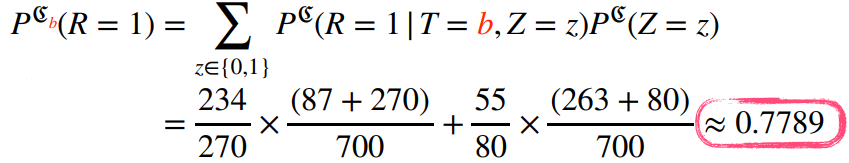딥러닝에서 확률론이 필요한 이유
DL은 확률론 기반의 기계학습 이론이 바탕
기계학습에서 사용되는 손실함수(loss function)의 작동 원리는 데이터 공간을 통계적으로 해석하여 유도
데이터의 초상화: 확률분포
이산확률변수 VS 연속확률변수
확률변수는 확률분포 D \mathscr{D} D
이산확률변수: 확률변수가 가질 수 있는 경우의 수를 모두 고려하여 확률을 더해 모델링P ( X ∈ A ) = ∑ x ∈ A P ( X = x ) \mathbb{P}(X\in A)=\displaystyle\sum_{\bold{x}\in A}P(X=\bold{x}) P ( X ∈ A ) = x ∈ A ∑ P ( X = x )
연속확률변수: 데이터 공간에 정의된 확률변수의 밀도(density) 위에서의 적분을 통해 모델링P ( X ∈ A ) = ∫ A P ( x ) d x ( P ( x ) = lim h → 0 P ( x − h ≤ X ≤ x + h ) 2 h ) \mathbb{P}(X\in A) = \displaystyle\int_AP(\bold{x})d\bold{x}\quad(P(\bold{x})=\underset{h\rightarrow0}{\textrm{lim}}\frac{\mathbb{P(\bold{x}-h\leq \textit{X}\leq\bold{x}+h)}}{2h}) P ( X ∈ A ) = ∫ A P ( x ) d x ( P ( x ) = h → 0 lim 2 h P ( x − h ≤ X ≤ x + h ) )
확률분포
데이터 공간: X × Y \mathscr{X}\times\mathscr{Y} X × Y
데이터 공간에서 데이터를 추출하는 분포: D \mathscr{D} D
데이터(확률 변수): ( x , y ) ∼ D (\bold{x},y)\sim\mathscr{D} ( x , y ) ∼ D
( x , y ) ∈ X × Y (\bold{x},y)\in\mathscr{X}\times\mathscr{Y} ( x , y ) ∈ X × Y
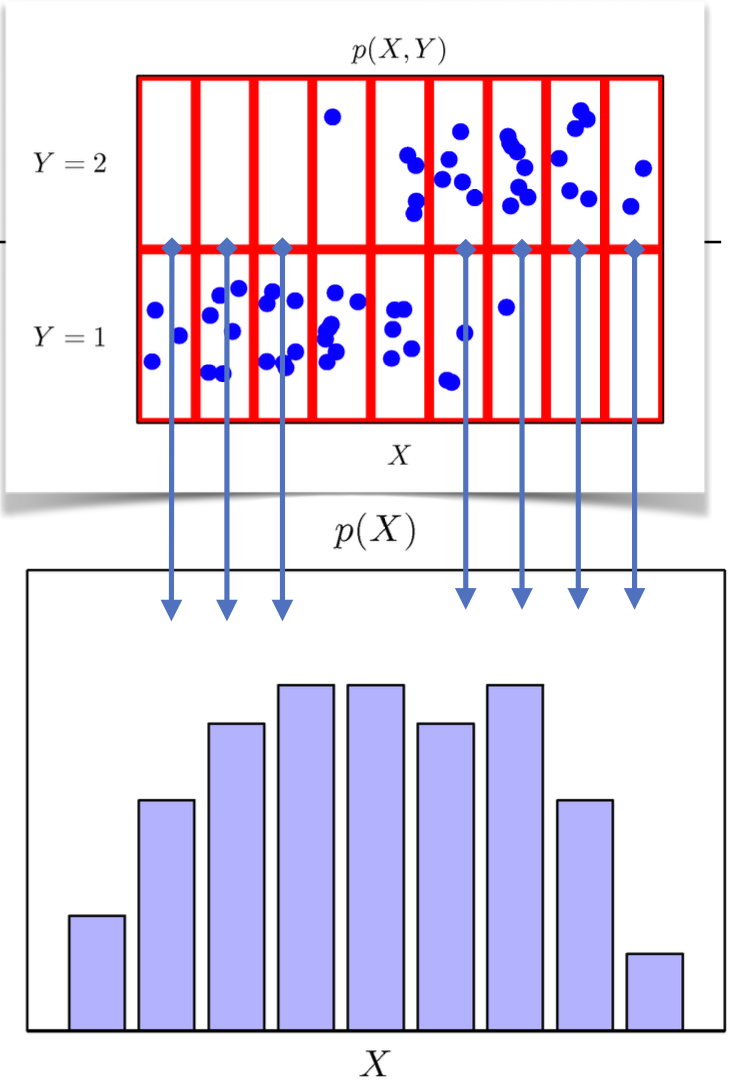
결합분포 P ( x , y ) P(\bold{x},y) P ( x , y ) D \mathscr{D} D
P ( x ) P(\bold{x}) P ( x ) x \bold{x} x y y y P ( x ) = ∑ y P ( x , y ) P ( x ) = ∫ y P ( x , y ) d y P(\bold{x})=\displaystyle\sum_yP(\bold{x},y) \\ P(\bold{x})=\displaystyle\int_yP(\bold{x},y)\textrm{d}y P ( x ) = y ∑ P ( x , y ) P ( x ) = ∫ y P ( x , y ) d y
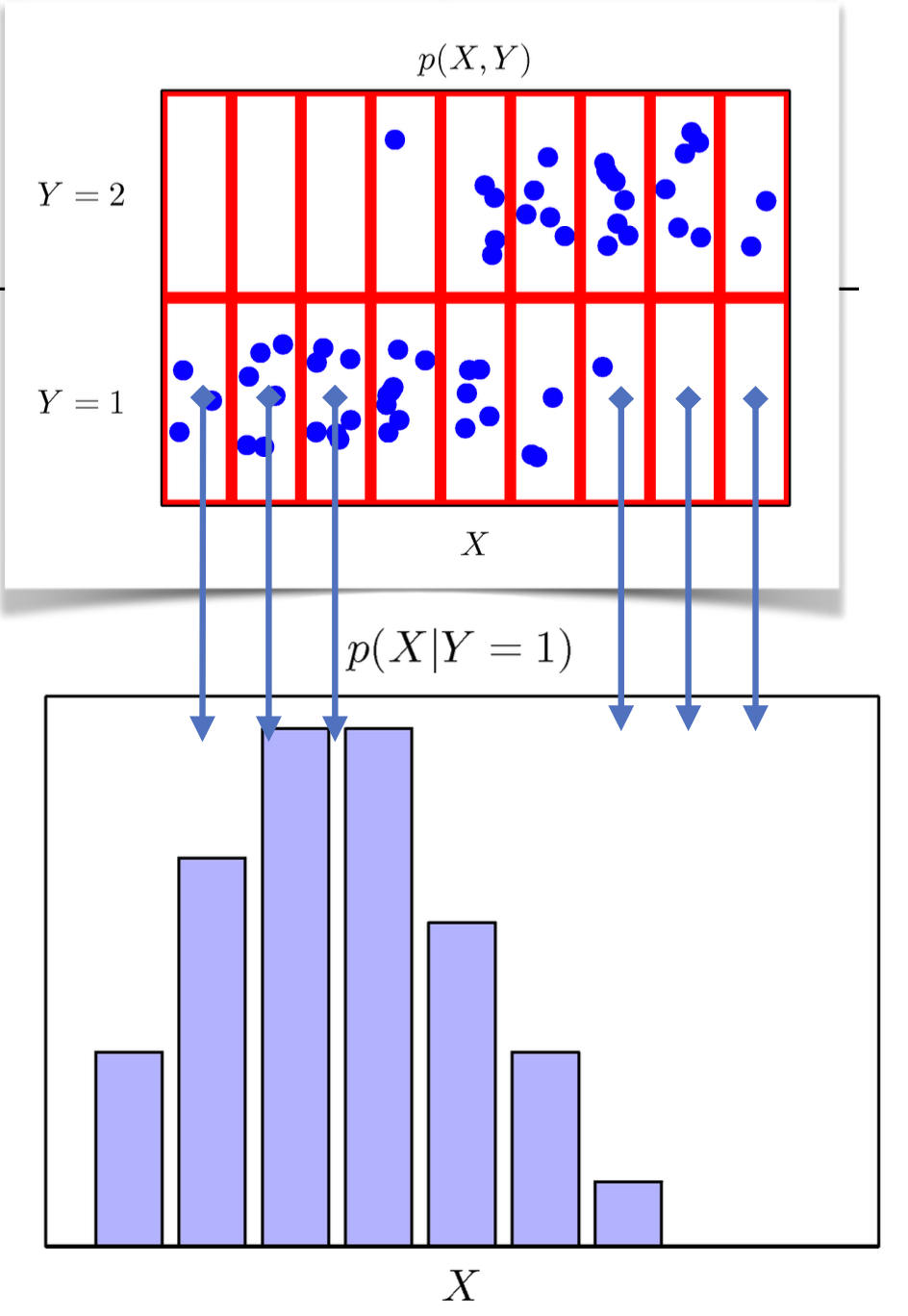
조건부확률분포 P ( x ∣ y ) P(\bold{x}\,|\,y) P ( x ∣ y ) x \bold{x} x y y y
P ( x ∣ y ) P(\bold{x}\,|\,y) P ( x ∣ y ) P ( y ∣ x ) P(y\,|\,\bold{x}) P ( y ∣ x ) x \bold{x} x y y y
조건부확률과 기계학습
로지스틱 회귀에서 사용했던 선형모델과 소프트맥스 함수의 결합 은 데이터에서 추출된 패턴을 기반으로 확률을 해석 하는데 사용됨
회귀 문제의 경우 조건부 기대값 E [ y ∣ x ] \mathbb{E}[y\,|\,\bold{x}] E [ y ∣ x ]
조건부 기대값은 E ∥ y − f ( x ) ∥ 2 \mathbb{E}\|y-f(\bold{x})\|_2 E ∥ y − f ( x ) ∥ 2 f ( x ) f(\bold{x}) f ( x )
분류 문제에서 softmax ( W ϕ + b ) \textrm{softmax}(\bold{W}\phi+\bold{b}) softmax ( W ϕ + b ) x \bold{x} x ϕ ( x ) \phi(\bold{x}) ϕ ( x ) W \bold{W} W P ( y ∣ x ) P(y\,|\,\bold{x}) P ( y ∣ x ) P ( y ∣ ϕ ( x ) P(y\,|\,\phi(\bold{x}) P ( y ∣ ϕ ( x )
딥러닝은 다층 신경망(MLP)을 이용해 데이터로부터 특징 패턴 ϕ \phi ϕ
기대값(Expectation)
확률분포가 주어지면, 데이터를 분석하는데 사용 가능한 여러 통계적 범함수(statistical functional)를 계산할 수 있음
기대값(expectation)은 데이터를 대표하는 통계량이면서, 동시에 확률분포를 통해 다른 통계적 범함수를 계산하는데 사용됨E x ∼ P ( x ) [ f ( x ) ] = ∑ x ∈ X f ( x ) P ( x ) = ∫ X f ( x ) P ( x ) d x \mathbb{E}_{\bold{x}\sim P(\bold{x})}[f(\bold{x})] = \displaystyle\sum_{\bold{x}\in\mathcal{X}}f(\bold{x})P(\bold{x}) = \displaystyle\int_\mathcal{X}f(\bold{x})P(\bold{x})\textrm{d}\bold{x} E x ∼ P ( x ) [ f ( x ) ] = x ∈ X ∑ f ( x ) P ( x ) = ∫ X f ( x ) P ( x ) d x
분산, 첨도, 공분산 등 여러 통계량 계산 가능
몬테카를로 샘플링(Monte Carlo Simulation)
기계학습의 많은 문제들은 확률분포를 명시적으로 알 수 없음
이때 데이터를 이용해 기대값을 계산하기 위하여 사용하는 방법이 바로 몬테카를로 샘플링E x ∼ P ( x ) [ f ( x ) ] ≈ 1 N ∑ i = 1 N f ( x ( i ) ) ( x ( i ) ∼ i.i.d P ( x ) ) \mathbb{E}_{\bold{x}\sim P(\bold{x})}[f(\bold{x})] \approx \displaystyle\frac{1}{N}\sum^N_{i=1}f(\bold{x}^{(i)}) \quad (\bold{x}^{(i)}\overset{\textrm{i.i.d}}{\sim}P(\bold{x})) E x ∼ P ( x ) [ f ( x ) ] ≈ N 1 i = 1 ∑ N f ( x ( i ) ) ( x ( i ) ∼ i.i.d P ( x ) )
몬테카를로 샘플링은 독립추출만 보장된다면 대수의 법칙(law of large number)에 의해 수렴성을 보장
예제: [ − 1 , 1 ] [-1,\,1] [ − 1 , 1 ] f ( x ) = e − x 2 f(x)=e^{-x^2} f ( x ) = e − x 2
해석적으로는 불가능함
import numpy as np
def mc_int ( fun, low, high, sample_size= 100 , repeat= 10 ) :
int_len = np. abs ( high - low)
stat = [ ]
for _ in range ( repeat) :
x = np. random. uniform( low= low, high= high, size= sample_size)
fun_x = fun( x)
int_val = int_len * np. mean( fun_x)
stat. append( int_val)
return np. mean( stat) , np. std( stat)
def f ( x) :
return np. exp( - x** 2 )
print ( mc_int( f, low= - 1 , high= 1 , sample_size= 10000 , repeat= 100 )
모수
통계적 모델링: 적절한 가정 위에서 확률 분포를 추정(inference)하는 것이 목표
유한한 개수의 데이터만 관찰해서는 모집단의 분포를 정확하게 알아내는 것이 불가능
근사적으로 확률분포를 추정하는 수 밖에 없음
예측 모형은 데이터와 불확실성을 고려해 위험(risk)을 최소화하는 것이 목표
모수적(parametric) 방법론 : 데이터가 특정 확률분포를 따른다고 선험적으로 가정하고, 그 분포를 결정하는 모수(parameter)를 추정하는 방법
확률분포를 가정하지 않고 데이터에 따라 모델 구조 및 모수 개수가 유연하게 바꾸는 경우 비모수(non-parametric) 방법론이라 함 ⇒ 기계학습의 많은 방법론이 비모수 방법론
확률분포 가정하기
히스토그램 및 데이터 특징에 기반하여 확률분포를 가정할 수 있음
데이터가 2개 값(0 또는 1)만 가지는 경우 → Bernoulli dist.
데이터가 n개의 이산값을 가지는 경우 → Category dist.
데이터가 [ 0 , 1 ] [0,1] [ 0 , 1 ]
데이터가 0 이상의 값을 가지는 경우 → Gamma dist., Log-normal dist.
데이터가 R \mathbb{R} R
기계적으로 가정하는 것은 안되고, 데이터를 생성하는 원리를 먼저 고려해야 함
데이터 기반 모수 추정
데이터의 확률분포를 가정했다면 모수를 추정할 수 있음
예를 들어 정규분포의 모수는 평균 μ \mu μ σ 2 \sigma^2 σ 2 X ˉ = 1 N ∑ i = 1 N X i , E [ X ˉ ] = μ S 2 = 1 N − 1 ∑ i = 1 N ( X i − X ˉ ) 2 , E [ S 2 ] = σ 2 \bar{X} = \displaystyle\frac{1}{N}\sum^N_{i=1}X_i, \quad \mathbb{E}[\bar{X}]=\mu \\ S^2 = \frac{1}{N-1}\sum^N_{i=1}(X_i-\bar{X})^2, \quad \mathbb{E}[S^2]=\sigma^2 X ˉ = N 1 i = 1 ∑ N X i , E [ X ˉ ] = μ S 2 = N − 1 1 i = 1 ∑ N ( X i − X ˉ ) 2 , E [ S 2 ] = σ 2
표본분산 계산 시 N N N N − 1 N-1 N − 1
통계량의 확률분포는 표집분포(sampling distribution)이라 하며, N N N X ˉ \bar{X} X ˉ N ( μ , σ 2 / N ) \mathscr{N}(\mu,\sigma^2/N) N ( μ , σ 2 / N )
모집단이 정규분포를 따르지 않더라도 성립하며, 이를 중심극한정리 (central limit theorem)이라 함
최대가능도 추정(Maximum Likelihood Estimation, MLE)
확률분포마다 모수가 다르므로, 추정에 적절한 통계량이 달라지게 됨
가장 효과적인 모수 추정 방법으로 알려진 방법론 중 하나가 바로 MLEθ ^ M L E = argmax θ L ( θ ; x ) = argmax θ P ( x i ∣ θ ) \hat{\theta}_{MLE} = \underset{\theta}{\textrm{argmax}}\,L(\theta;\,\bold{x}) = \underset{\theta}{\textrm{argmax}}\,P(\bold{x}_i|\theta) θ ^ M L E = θ argmax L ( θ ; x ) = θ argmax P ( x i ∣ θ )
로그가능도(Log-Likelihood)
데이터 집합 X \bold{X} X L ( θ ; X ) = ∏ i = 1 n P ( x i ∣ θ ) ⇒ log L ( θ ; X ) = ∑ i = 1 n log P ( x i ∣ θ ) L(\theta;\,\bold{X})=\displaystyle\prod^n_{i=1}P(\bold{x}_i|\,\theta) \quad\Rightarrow\quad \textrm{log}\,L(\theta;\,\bold{X}) = \sum^n_{i=1}\textrm{log}\,P(\bold{x}_i|\,\theta) L ( θ ; X ) = i = 1 ∏ n P ( x i ∣ θ ) ⇒ log L ( θ ; X ) = i = 1 ∑ n log P ( x i ∣ θ )
데이터의 숫자가 커진다면 컴퓨터의 정확도로는 가능도를 계산하는 것이 불가해짐
하지만 데이터가 독립일 경우, 가능도의 곱셈을 로그가능도의 덧셈으로 변환할 수 있기 때문에 연산량이 작아짐
경사하강법에 기반해 가능도 최적화시 로그가능도를 이용하면 미분 연산량이 O ( n 2 ) O(n^2) O ( n 2 ) O ( n ) O(n) O ( n )
손실함수의 경우 대개 음의 로그가능도(negative log-likelihood)를 최적화
MLE 예시: 정규분포
정규분포를 따르는 확률변수 X X X { x 1 , … , x n } \{x_1,\dots,x_n\} { x 1 , … , x n } θ ^ M L E = argmax θ L ( θ ; x ) = argmax μ , σ 2 P ( X ∣ μ , σ 2 ) \hat{\theta}_{MLE} = \underset{\theta}{\textrm{argmax}}\,L(\theta;\,\bold{x}) = \underset{\mu,\sigma^2}{\textrm{argmax}}\,P(\bold{X}|\mu,\,\sigma^2) θ ^ M L E = θ argmax L ( θ ; x ) = μ , σ 2 argmax P ( X ∣ μ , σ 2 )
θ = ( μ , σ ) \theta=(\mu,\,\,\sigma) θ = ( μ , σ ) log L ( θ ; X ) = ∑ i = 1 n log P ( x i ∣ θ ) \textrm{log}\,L(\theta;\,\bold{X})=\displaystyle\sum^n_{i=1}\textrm{log}\,P(x_i|\,\theta) log L ( θ ; X ) = i = 1 ∑ n log P ( x i ∣ θ )
log L ( θ ; X ) = ∑ i = 1 n log P ( x i ∣ θ ) = ∑ i = 1 n log 1 2 π σ 2 e − ∣ x i − μ ∣ 2 2 σ 2 = − n 2 log 2 π σ 2 − ∑ i = 1 n ∣ x i − μ ∣ 2 2 σ 2 \textrm{log}\,L(\theta;\,\bold{X}) = \displaystyle\sum^n_{i=1}\textrm{log}\,P(x_i|\,\theta) \\= \sum^n_{i=1}\textrm{log}\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{|x_i-\mu|^2}{2\sigma^2}} = -\frac{n}{2}\textrm{log}\,2\pi\sigma^2-\sum^n_{i=1}\frac{|x_i-\mu|^2}{2\sigma^2} log L ( θ ; X ) = i = 1 ∑ n log P ( x i ∣ θ ) = i = 1 ∑ n log 2 π σ 2 1 e − 2 σ 2 ∣ x i − μ ∣ 2 = − 2 n log 2 π σ 2 − i = 1 ∑ n 2 σ 2 ∣ x i − μ ∣ 2
이를 미분하면,
0 = ∂ log L ∂ μ = − ∑ i = 1 n x i − μ σ 2 ⇒ μ ^ M L E = 1 n ∑ i = 1 n x i 0 = ∂ log L ∂ σ = − n σ + 1 σ 3 ∑ i = 1 n ∣ x i − μ ∣ 2 ⇒ σ ^ M L E 2 = 1 n ∑ i = 1 n ( x i − μ ) 2 0 = \displaystyle\frac{\partial\,\textrm{log}\,L}{\partial\mu} = -\sum^n_{i=1}\frac{x_i-\mu}{\sigma^2} \quad\Rightarrow\quad \hat{\mu}_{MLE} = \frac{1}{n}\sum^n_{i=1}x_i \\ 0 = \frac{\partial\,\textrm{log}\,L}{\partial\sigma}=-\frac{n}{\sigma}+\frac{1}{\sigma^3}\sum^n_{i=1}|x_i-\mu|^2 \quad\Rightarrow\quad \hat{\sigma}^2_{MLE} = \frac{1}{n}\sum^n_{i=1}(x_i-\mu)^2 0 = ∂ μ ∂ log L = − i = 1 ∑ n σ 2 x i − μ ⇒ μ ^ M L E = n 1 i = 1 ∑ n x i 0 = ∂ σ ∂ log L = − σ n + σ 3 1 i = 1 ∑ n ∣ x i − μ ∣ 2 ⇒ σ ^ M L E 2 = n 1 i = 1 ∑ n ( x i − μ ) 2
위 식을 만족하는 μ \mu μ σ \sigma σ
다만 unbiased 추정량을 보장하지는 않음 (σ ^ M L E 2 \hat{\sigma}^2_{MLE} σ ^ M L E 2
MLE 예시: 카테고리 분포
카테고리 분포 Multinoulli ( x ; p 1 , … , p d ) \textrm{Multinoulli}(\bold{x};\,p_1,\dots,p_d) Multinoulli ( x ; p 1 , … , p d ) X X X { x 1 , … , x n } \{\bold{x}_1,\dots,\bold{x}_n\} { x 1 , … , x n } θ ^ M L E = argmax p 1 , … , p d log P ( x i ∣ θ ) = argmax p 1 , … , p d log ( ∏ i = 1 n ∏ k = 1 d p k x i , k ) ( ∑ k = 1 d p k = 1 ) \displaystyle\hat{\theta}_{MLE} = \underset{p_1,\dots,p_d}{\textrm{argmax}}\,\textrm{log}\,P(\bold{x}_i|\,\theta) = \underset{p_1,\dots,p_d}{\textrm{argmax}}\,\textrm{log}(\prod^n_{i=1}\prod^d_{k=1}p^{x_{i,\,k}}_k) \quad (\sum^d_{k=1}p_k=1) θ ^ M L E = p 1 , … , p d argmax log P ( x i ∣ θ ) = p 1 , … , p d argmax log ( i = 1 ∏ n k = 1 ∏ d p k x i , k ) ( k = 1 ∑ d p k = 1 )
이때 n k = ∑ i = 1 n x i , k n_k=\displaystyle\sum^n_{i=1}x_{i,\,k} n k = i = 1 ∑ n x i , k log ( ∏ i = 1 n ∏ k = 1 d p k i , k ) = ∑ k = 1 d ( ∑ i = 1 n x i , k ) log p k = ∑ k = 1 d n k log p k ⇒ L ( p 1 , … , p k , λ ) = ∑ k = 1 d n k log p k + λ ( 1 − ∑ k p k ) 0 = ∂ L ∂ p k = n k p k − λ , 0 = ∂ L ∂ λ = 1 − ∑ k = 1 d p k ⇒ p k = n k ∑ k = 1 d n k \displaystyle \textrm{log}(\prod^n_{i=1}\prod^d_{k=1}p^{i,\,k}_k) = \sum^d_{k=1}(\sum^n_{i=1}x_{i,\,k})\textrm{log}\,p_k = \sum^d_{k=1}n_k\textrm{log}\,p_k \\\Rightarrow \mathcal{L}(p_1,\dots,p_k,\lambda) = \sum^d_{k=1}n_k\textrm{log}\,p_k+\lambda(1-\sum_kp_k) \\ 0 = \frac{\partial\,\mathcal{L}}{\partial\,p_k}=\frac{n_k}{p_k}-\lambda, \quad 0 = \frac{\partial\,\mathcal{L}}{\partial\,\lambda} = 1-\sum^d_{k=1}p_k \\\Rightarrow p_k = \frac{n_k}{\sum^d_{k=1}n_k} log ( i = 1 ∏ n k = 1 ∏ d p k i , k ) = k = 1 ∑ d ( i = 1 ∑ n x i , k ) log p k = k = 1 ∑ d n k log p k ⇒ L ( p 1 , … , p k , λ ) = k = 1 ∑ d n k log p k + λ ( 1 − k ∑ p k ) 0 = ∂ p k ∂ L = p k n k − λ , 0 = ∂ λ ∂ L = 1 − k = 1 ∑ d p k ⇒ p k = ∑ k = 1 d n k n k
DL에서의 MLE
DL 모델의 가중치가 θ = ( W ( 1 ) , … , W ( L ) ) \theta=(\bold{W}^{(1)},\dots,\bold{W}^{(L)}) θ = ( W ( 1 ) , … , W ( L ) ) ( p 1 , … , p K ) (p_1,\dots,p_K) ( p 1 , … , p K )
One-hot vector로 표현한 정답 레이블 y = ( y 1 , … , y K ) \bold{y}=(y_1,\dots,y_K) y = ( y 1 , … , y K ) θ ^ M L E = argmax θ 1 n ∑ i = 1 n ∑ k = 1 K y i , k log ( M L E θ ( x i ) k ) \displaystyle \hat{\theta}_{MLE}=\underset{\theta}{\textrm{argmax}}\frac{1}{n}\sum^n_{i=1}\sum^K_{k=1}y_{i,\,k}\,\textrm{log}(MLE_{\theta}(\bold{x}_i)_k) θ ^ M L E = θ argmax n 1 i = 1 ∑ n k = 1 ∑ K y i , k log ( M L E θ ( x i ) k )
확률분포 간 거리
기계학습에서 사용되는 손실함수들은 모델이 학습하는 확률분포와, 데이터에서 관찰되는 확률분포 사이 거리를 통해 유도됨
데이터 공간에 두 확률분포 P ( x ) P(\bold{x}) P ( x ) Q ( x ) Q(\bold{x}) Q ( x )
총 변동 거리(total variation distance, TV)
쿨백-라이블러 발산(Kullback-Leibler divergence, KL)K L ( P ∥ Q ) = ∑ x ∈ X P ( x ) log ( P ( x ) Q ( x ) ) = ∫ X P ( x ) log ( P ( x ) Q ( x ) ) d x = − E x ∼ P ( x ) [ log Q ( x ) ] + E x ∼ P ( x ) [ log P ( x ) ] \mathbb{KL}(P\|Q) = \displaystyle \sum_{\bold{x}\in\mathcal{X}}P(\bold{x})\textrm{log}(\frac{P(\bold{x})}{Q(\bold{x})}) = \int_\mathcal{X}P(\bold{x})\textrm{log}(\frac{P(\bold{x})}{Q(\bold{x})})\textrm{d}\bold{x} \\= -\mathbb{E}_{\bold{x}\sim P(\bold{x})}[\textrm{log}\,Q(\bold{x})] + \mathbb{E}_{\bold{x}\sim P(\bold{x})}[\textrm{log}\,P(\bold{x})] K L ( P ∥ Q ) = x ∈ X ∑ P ( x ) log ( Q ( x ) P ( x ) ) = ∫ X P ( x ) log ( Q ( x ) P ( x ) ) d x = − E x ∼ P ( x ) [ log Q ( x ) ] + E x ∼ P ( x ) [ log P ( x ) ]
− E x ∼ P ( x ) [ log Q ( x ) ] -\mathbb{E}_{\bold{x}\sim P(\bold{x})}[\textrm{log}\,Q(\bold{x})] − E x ∼ P ( x ) [ log Q ( x ) ] E x ∼ P ( x ) [ log P ( x ) ] \mathbb{E}_{\bold{x}\sim P(\bold{x})}[\textrm{log}\,P(\bold{x})] E x ∼ P ( x ) [ log P ( x ) ] 분류 문제에서 정답을 P P P Q Q Q
바슈타인 거리(Wasserstein distance)
조건부 확률
베이즈 통계학을 이해하기 위해서는, 조건부 확률의 개념을 이해해야 함P ( A ∩ B ) = P ( B ) P ( A ∣ B ) P ( B ∣ A ) = P ( A ∩ B ) P ( A ) = P ( B ) P ( A ∣ B ) P ( A ) P(A\cap B)=P(B)P(A|B) \\ P(B|A)=\frac{P(A\cap B)}{P(A)}=P(B)\frac{P(A|B)}{P(A)} P ( A ∩ B ) = P ( B ) P ( A ∣ B ) P ( B ∣ A ) = P ( A ) P ( A ∩ B ) = P ( B ) P ( A ) P ( A ∣ B )
베이즈 정리는 조건부 확률을 이용하여 정보를 갱신하는 방법을 알려줌 ⇒ A A A P ( B ) P(B) P ( B ) P ( B ∣ A ) P(B|A) P ( B ∣ A )
베이즈 정리
예제
🖍️ COVID-99의 발병률이 10%로 알려져있다. COVID-99에 실제로 걸렸을 때 검진될 확률은 99%, 실제로 걸리지 않았을 때 오검진될 확률이 1%라고 할 때, 어떤 사람이 질병에 걸렸다고 검진 결과가 나왔다면 이 사람이 실제로 COVID-99에 감염되었을 확률은?
θ \theta θ D D D
P ( θ ∣ D ) = P ( θ ) P ( D ∣ θ ) P ( D ) P(\theta|D)=P(\theta)\frac{P(D|\theta)}{P(D)} P ( θ ∣ D ) = P ( θ ) P ( D ) P ( D ∣ θ )
P ( θ ∣ D ) P(\theta|D) P ( θ ∣ D ) P ( θ ) P(\theta) P ( θ ) P ( D ∣ θ ) P(D|\theta) P ( D ∣ θ )
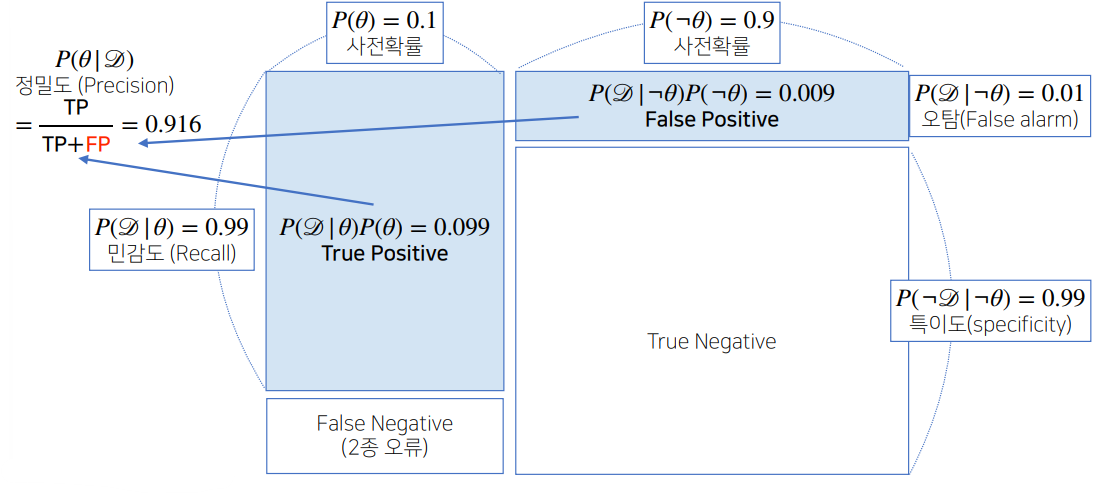
P ( D ∣ θ c ) P(D|\theta^c) P ( D ∣ θ c ) P ( D ) P(D) P ( D ) P ( D ) = ∑ θ P ( D ∣ θ ) P ( θ ) = 0.99 × 0.1 + 0.01 × 0.9 = 0.108 P ( θ ∣ D ) = 0.1 × 0.99 0.108 ≈ = 0.916 P(D)=\displaystyle\sum_{\theta}P(D|\theta)P(\theta)=0.99\times0.1+0.01\times0.9=0.108 \\ P(\theta|D)=0.1\times\frac{0.99}{0.108}\approx=0.916 P ( D ) = θ ∑ P ( D ∣ θ ) P ( θ ) = 0 . 9 9 × 0 . 1 + 0 . 0 1 × 0 . 9 = 0 . 1 0 8 P ( θ ∣ D ) = 0 . 1 × 0 . 1 0 8 0 . 9 9 ≈ = 0 . 9 1 6 P ( D ∣ θ c ) P(D|\theta^c) P ( D ∣ θ c )
우선, P ( D ∣ θ ) + P ( D ∣ θ c ) ≠ 1 P(D|\theta)+P(D|\theta^c)\neq1 P ( D ∣ θ ) + P ( D ∣ θ c ) = 1 P ( D ) = ∑ θ P ( D ∣ θ ) P ( θ ) = 0.99 × 0.1 + 0.1 × 0.9 = 0.189 P ( θ ∣ D ) = 0.1 × 0.99 0.189 ≈ = 0.524 P(D)=\displaystyle\sum_{\theta}P(D|\theta)P(\theta)=0.99\times0.1+0.1\times0.9=0.189 \\ P(\theta|D)=0.1\times\frac{0.99}{0.189}\approx=0.524 P ( D ) = θ ∑ P ( D ∣ θ ) P ( θ ) = 0 . 9 9 × 0 . 1 + 0 . 1 × 0 . 9 = 0 . 1 8 9 P ( θ ∣ D ) = 0 . 1 × 0 . 1 8 9 0 . 9 9 ≈ = 0 . 5 2 4
조건부 확률의 시각화
정보 갱신
베이즈 정리를 통해, 새로운 데이터가 들어왔을 때, 앞서 계산한 사후확률을 사전확률로 사용하여 갱신된 사후확률을 계산할 수 있음
앞서 COVID-99 판정을 받은 사람이 두 번째 검진을 받았을 때에도 양성이 나온 경우, 진짜로 COVID-99에 걸렸을 확률은? → 갱신된 사후확률에 대한 문제P ( D ∗ ) = 0.99 × 0.524 + 0.1 × 0.476 ≈ 0.566 P ( θ ∣ D ∗ ) = 0.524 × 0.99 0.566 ≈ 0.917 P(D^*)=0.99\times0.524+0.1\times0.476\approx0.566 \\ P(\theta|D^*)=0.524\times\frac{0.99}{0.566}\approx0.917 P ( D ∗ ) = 0 . 9 9 × 0 . 5 2 4 + 0 . 1 × 0 . 4 7 6 ≈ 0 . 5 6 6 P ( θ ∣ D ∗ ) = 0 . 5 2 4 × 0 . 5 6 6 0 . 9 9 ≈ 0 . 9 1 7
인과관계
조건부 확률은 유용한 통계적 해석을 제공하나, 인과관계(causality)를 추론할 때 함부로 사용할 수 없음
인과관계는 데이터 분포의 변화에 민감하지 않은 강건한 예측 모델을 만들 때 필요
인과관계의 파악을 위해서는 중첩요인(confounding factor) Z Z Z
Z Z Z
예제
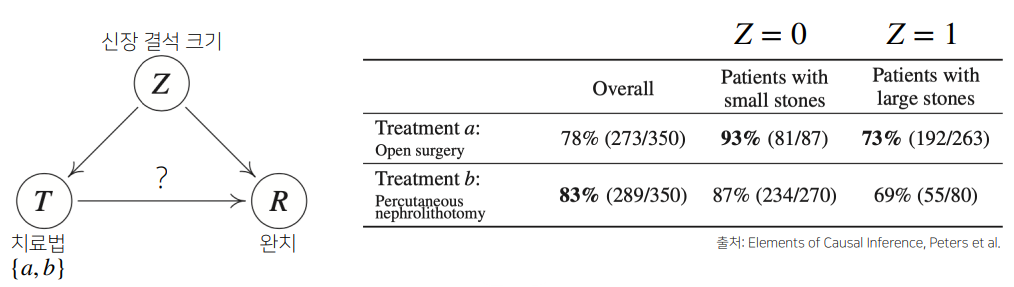
🖍️ 신장 결석의 크기에 따른 치료법 선택
$a$는 개복 수술, $b$는 주사 치료
전체 확률을 보면 치료법 b b b
하지만 신장 결석이 작을 때와 클 때 모두 치료법 a a a b b b
Simpson’s paradox라고 하는 매우 유명한 통계적 역설 문제
신장 결석 크기에 상관 없이 모든 환자가 치료법 a a a b b b
조정(intervention)을 통해 중첩 효과를 가진 신장 결석 크기 Z Z Z
모든 환자가 치료법 a a a
모든 환자가 치료법 b b b