Direct Preference Optimization (DPO) 간단 정리

개요

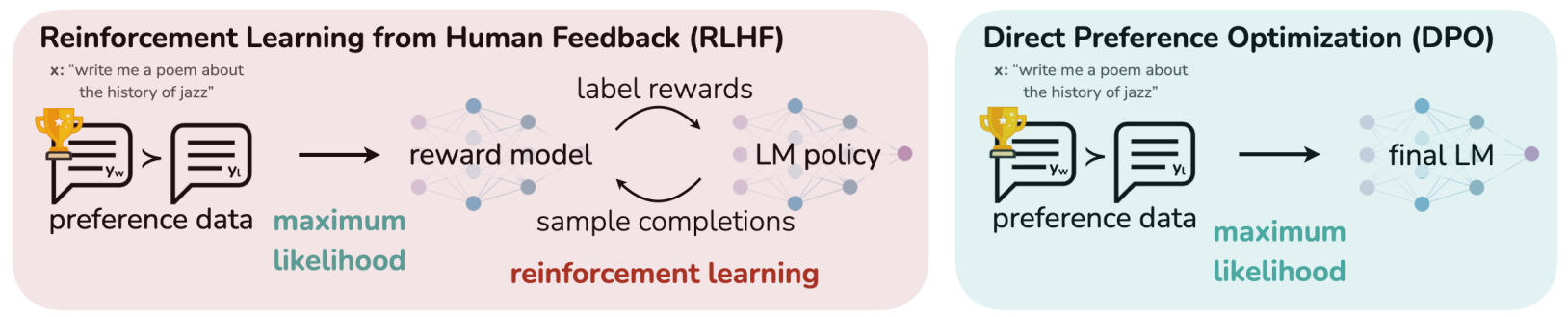
• DPO는 PPO와 같은 강화학습 policy, 즉 reward 모델링을 사용하지 않고 reward 함수와 policy만을 매핑해 human preference에 맞춰 최적화할 수 있는 방법
  • RLHF보다 요약 및 single-turn task에서 더 좋은 성능
• RLHF에서 최종 loss를 reward로 받아 PPO 알고리즘으로 업데이트하는 과정을 없애고, RLHF의 reward 모델링 단계에서 LM을 바로 업데이트하는 형태로 변형
  • ‘Reward’ 라는 말 자체가 RL term이라 DPO는 RL을 사용하지 않는다는 점을 강조하기 위해 preference 모델링이라는 말을 사용한 듯

DPO의 메커니즘

Optimal Policy $\pi$ 구하기

• RLHF의 RL finetuning 단계에서 사용하는 최종 loss를 조금 변형
  $\max_\pi\mathbb{E}_{x\sim\mathcal{D},y\sim\pi}[r(x,y)]-\beta\mathbb{D}_\text{KL}[\pi(y|x)\;||\;\pi_\text{ref}(y|x)] \\ =\max_\pi\mathbb{E}_{x\sim\mathcal{D}}\mathbb{E}_{y\sim\pi(y|x)}[r(x,y)-\beta\log\frac{\pi(y|x)}{\pi_\text{ref}(y|x)}] \\ =\min_\pi\mathbb{E}_{x\sim\mathcal{D}}\mathbb{E}_{y\sim\pi(y|x)}[\log\frac{\pi(y|x)}{\pi_\text{ref}(y|x)}-\frac{1}{\beta}r(x,y)] \\ =\min_\pi\mathbb{E}_{x\sim\mathcal{D}}\mathbb{E}_{y\sim\pi(y|x)}[\log\frac{\pi(y|x)}{\frac{1}{Z(x)}\pi_\text{ref}(y|x)\exp(\frac{1}{\beta}r(x,y))}-\log Z(x)]$
  • $Z$는 업데이트 타겟 모델인 $\pi$와는 무관한 partition function
    $Z(x)=\sum_y\pi_\text{ref}(y|x)\exp(\frac{1}{\beta}r(x,y))$
• 위 과정을 통해 새로운 optimal policy $\pi^*$를 구할 수 있음
  $\pi^*(y|x)=\frac{1}{Z(x)}\pi_\text{ref}(y|x)\exp(\frac{1}{\beta}r(x,y))$
  • 위 term을 최대화하면 위 RLHF loss 수식의 전체 loss를 최소화하는 것과 같기 때문
  • 이 $\pi^*$를 RLHF loss 수식에 다시 대입해보면, $\min_\pi\mathbb{E}$ 내부의 term이 $\log\frac{\pi(y|x)}{\pi^*(y|x)}-\log Z$가 되는데, 결국 이는 $\text{KL}(\frac{\pi}{\pi^*})$인 셈
  • 어차피 $Z$는 $\pi$와 무관한 term이고, DPO의 목표는 $\pi$의 최적화이기 때문에 $Z$ 관련 term은 날아가 결국 $\pi$가 $\pi^*$에 근접할 때 loss가 가장 작다는 의미가 됨

Reward Model 다시 쓰기

• 위에서 구한 optimal policy $\pi^*$ 수식의 양 변에 로그를 취하고, $r(x,y)$를 좌변으로 옮기면 아래와 같은 수식을 도출할 수 있음
  $r(x,y)=\beta\log\frac{\pi_r(y|x)}{\pi_\text{ref}(y|x)}+\beta\log Z(x)$
  • Policy를 통해 reward를 나타낼 수 있다는 것
• RL 모델링에서 사용했던 Bradley-Terry 모델의 $r$과 $r^*$에 각각 위 식을 대입해보면, DPO 만의 새로운 preference, 즉 reward 모델을 도출할 수 있음
  $p^*(y_1\succ y_2|x)=\frac{1}{1+\exp(\beta\log\frac{\pi^*(y_2|x)}{\pi_\text{ref}(y_2|x)}-\beta\log\frac{\pi^*(y_1|x)}{\pi_\text{ref}(y_1|x)})}$
• RLHF의 최종 loss에도 이를 적용하면, reward 모델을 직접 두지 않고도 LM output을 통해 최종적인 DPO loss를 구할 수 있다는 것이 이 논문의 차별점
  $\mathcal{L}_\text{DPO}(\pi_\theta;\pi_\text{ref})=-\mathbb{E}_{(x,y_w,y_l)\sim\mathcal{D}}[\log\sigma(\beta\log\frac{\pi_\theta(y_w|x)}{\pi_\text{ref}(y_w|x)}-\beta\log\frac{\pi_\theta(y_l|x)}{\pi_\text{ref}(y_l|x)})]$

이론적 배경

• DPO에서 reward 모델이 필요없다는 주장을 뒷받침하는 근거는 “LM은 이미 reward 모델 역할을 하고 있다(제목과 동일)”는 것
• 이를 증명하기 위해서는 두 명제가 필요함
  • 명제 1: Bradley-Terry 모델에 근거한 두 reward 함수는 같은 클래스 $c$에서 같은 preference distribution을 따름
    $p_\pi(c)=p_{\pi_\text{ref}}(c)$
  • 명제 2: RL에서 같은 클래스 $c$에 대한 두 reward 함수의 optimal policy는 동일
    $\pi_{r}(x,y)=\pi_\text{ref}(x,y)$
    ⇒ 정의: $r(x,y)$와 $r'(x,y)$가 어떤 함수 $f(x)$에 대해 $r(x,y)-r'(x,y)=f(x)$를 만족한다면, $r$과 $r'$은 동일
• 단어 토큰 $y_1,\dots,y_K$에 대한 랭킹 $\tau$를 reward라고 가정하고, probability를 softmax라고 가정한다면, 명제 1은 아래 수식의 $r'(x,y)$에 $r(x,y)+f(x)$를 대입해 쉽게 증명 가능함
  $p_{r'}(\tau|y_1,\dots,y_K,x) =\prod^K_{k=1}\frac{\exp(r'(x,y_{\tau(k)}))}{\sum^K_{j=k}\exp(r'(x,y_{\tau(j)}))} =\prod^K_{k=1}\frac{\exp(r(x,y_{\tau(k)})+f(x))}{\sum^K_{j=k}\exp(r(x,y_{\tau(j)})+f(x))}$
  $=\prod^K_{k=1}\frac{\exp(f(x))\exp(r(x,y_{\tau(k)}))}{\exp(f(x))\sum^K_{j=k}\exp(r(x,y_{\tau(k)}))} =\prod^K_{k=1}\frac{\exp(r(x,y_{\tau(k)}))}{\sum^K_{j=k}\exp(r(x,y_{\tau(k)}))}$
  $=p_{r}(\tau|y_1,\dots,y_K,x)$
  • Probability를 계산하는 중에 어떤 term이 생략되는 지를 보면, performance 모델에 constraint를 주입해도 괜찮다는 것을 알 수 있음
• 명제 2의 경우엔 동일 클래스의 모든 reward 함수들이 하나의 optimal policy를 가진다는 의미이며, 이 또한 $r'(x,y)=r(x,y)+f(x)$를 이용하면 아래와 같이 증명 가능
  $\pi_{r'}(y|x) =\frac{1}{\sum_y\pi_\text{ref}(y|x)\exp(\frac{1}{\beta}r'(x,y))}\pi_\text{ref}(y|x)\exp(\frac{1}{\beta}r'(x,y)) \\ =\frac{1}{\sum_y\pi_\text{ref}(y|x)\exp(\frac{1}{\beta}(r(x,y)+f(x)))}\pi_\text{ref}(y|x)\exp(\frac{1}{\beta}(r(x,y)+f(x))) \\ =\frac{1}{\exp(\frac{1}{\beta}f(x))\sum_y\pi_\text{ref}(y|x)\exp(\frac{1}{\beta}r(x,y))}\pi_\text{ref}(y|x)\exp(\frac{1}{\beta}r(x,y))\exp(\frac{1}{\beta}f(x)) \\ =\frac{1}{\sum_y\pi_\text{ref}(y|x)\exp(\frac{1}{\beta}r(x,y))}\pi_\text{ref}(y|x)\exp(\frac{1}{\beta}r(x,y))$
  $=\pi_r(y|x)$
• 위 두 명제를 통해 $r(x,y)$가 모델의 policy인 $\pi_r$을 통해 표현될 수 있음을 보일 수 있음
  • DPO의 최적 policy이자 reward function인 $\pi_r(y|x)$에 대한 수식에서, $r(x,y)$와 $\pi_r$에 대해 $f(x)(x,y)=r(x,y)-\pi_r(x,y)$가 성립한다면, $r$과 $\pi$에 대한 두 명제도 성립할 것
• 임의의 projection $f$에 대해 아래 식을 가정했을 때, 이를 만족하는 $f$의 존재 여부만 알면 $r(x,y)$와 $\pi$가 동일하다고 말할 수 있음
  $f(r;\pi_\text{ref},\beta)(x,y)=r(x,y)-\beta\log\sum_y\pi_\text{ref}(y|x)\exp(\frac{1}{\beta}r(x,y))$
  • 위 식은 DPO의 reward 함수와 매우 유사하며, 그리고 이를 만족하는 $f$는 당연히 존재
    $f(r;\pi_\text{ref},\beta)(x,y)=\beta\log\frac{\pi_r(y|x)}{\pi_\text{ref}(y|x)}$
  • 즉, LM은 그 자체로 reward 모델 역할을 하고 있음