Direct Alignment from Preference (DAP) 방법론 간단 비교

개요

• RL은 기본적으로 SFT보다 불안정성이 매우 높은 학습 방법임
  • Hyperparameter의 영향이 큼
  • 좋은 reward를 위한 데이터 확보에 매우 많은 exploration이 필요함
  • 계산 비용 높음(policy + ref-policy + reward + value 모델)
• RL을 사용하지 않고 alignment를 수행하는 direct alignment from preference (DAP) 방법론들이 등장함

SLiC-HF (Sequence Likelihood Calibration, Deepmind 2023)

SLiC-HF: Sequence Likelihood Calibration with Human Feedback

• Positive/Negative 샘플을 특정 margin을 두고 hyperplane으로 구분하도록 만들어진 고전 ML 기법 SVM을 사용해 contrastive learning을 하는 것

• SLiC-HF loss function

  $\mathcal{L}(\theta)=\max(0,\delta-\log P_\theta(y^+|x)+\log P_\theta(y^-|x))-\lambda\log P_\theta(y_\text{ref}|x)$

  • $\max(0,\delta-\log P_\theta(y^+|x)+\log P_\theta(y^-|x))$

    • SVM의 hinge loss

  • $\lambda\log P_\theta(y_\text{ref}|x)$

    • Reference model regularizer
    • 보통 KL-divergence를 사용하지만 NLL 값도 유사한 효과를 가져온다고 함
    • KL-divergence보다 계산 비용 효율적

• 실험 결과

  • SFT 모델에 대해 80% 이상의 win rate
  • Human eval에서도 RLHF보다 높은 점수
  • 그러나 요약 task에 대해서만 평가됨 → Generalization 어려울 수도

DPO (Direct Preference Optimization, Stanford 2023)

Direct Preference Optimization: Your Language Model is Secretly a...

• RL objective를 수정해 SFT가 가능하도록 만든 방법론
• “KL-divergence regularizer가 존재하는 RL objective는 closed form이 반드시 존재한다”는 아이디어에서 시작
  $\underset{\pi_\theta}{\max}\mathbb{E}_{x\sim D,y\sim\pi_\theta(y|x)}[r_\phi(x,y)]-\beta D_{\text{KL}}[\pi_\theta(y|x)||\pi_\text{ref}(y|x)]$
  • 위 RL objective가 특정 값으로 수렴한다고 하면, optimal policy의 closed form $\pi_r$은 다음과 같음
    $\pi_r(y|x)=\frac{1}{Z(x)}\pi_\text{ref}(y|x)\exp(\frac{1}{\beta}r(x,y))$
  • 이때 $Z(x)$는 단순히 확률 합을 1로 만드는 scaling factor → 이를 정리해서 reward 수식 $r$로
    $r(x,y)=\beta\log\frac{\pi_r(y|x)}{\pi_\text{ref}(y|x)}+\beta\log Z(x)$
  • 여기에 RLHF의 reward model loss $\mathcal{L}_R$를 대입해주면
    $\mathcal{L}_R(r_\phi,D)=-\mathbb{E}_{(x,y_w,y_l)\sim D}[\log\sigma(r_\phi(x,y_w)-r_\phi(x,y_l))] \\ \downarrow \\\mathcal{L}_\text{DPO}(\pi_\theta;\pi_\text{ref})=-\mathbb{E}_{(x,y_w,y_l)\sim D}[\log\sigma(\beta\log\frac{\pi_\theta(y_w|x)}{\pi_\text{ref}(y_w|x)}-\beta\log\frac{\pi_\theta(y_l|x)}{\pi_\text{ref}(y_l|x)})]$
    • 위 $\mathcal{L}_\text{DPO}$를 최소화하면 별도의 reward function 학습 없이 policy 학습이 가능
    • $y_w$, $y_l$은 학습하는 preference 데이터에 이미 태깅되어 있기 때문에, SFT처럼 학습됨
• 사실 RL objective를 최대화하는 학습은 reward model이 있어야 가능한데, 이 reward model 학습을 위해 RL objective에서 얻은 closed form을 대입하는게 모순일 수 있음
  • 저자들이 주장하는 DPO loss function의 의의는 다음과 같음
  • 우선 DPO loss의 gradient는 다음과 같음
    $\nabla_\theta\mathcal{L}_\text{DPO}(\pi_\theta;\pi_\text{ref}) \\ -\beta\mathbb{E}_{(x,y_w,y_l)\sim D}[\sigma(\hat{r}_\theta(x,y_l)-\hat{r}_\theta(x,y_w))[\nabla_\theta\log\pi(y_w|x)-\nabla_\theta\log\pi(y_l|x)]]$
    • $\sigma(\hat{r}_\theta(x,y_l)-\hat{r}_\theta(x,y_w))$: Reward 추정이 틀린 경우 높은 가중
    • $\nabla_\theta\log\pi(y_w|x)$: $y_w$의 likelihood 증가
    • $\nabla_\theta\log\pi(y_l|x)$: $y_l$의 likelihood 감소
• 실험 결과
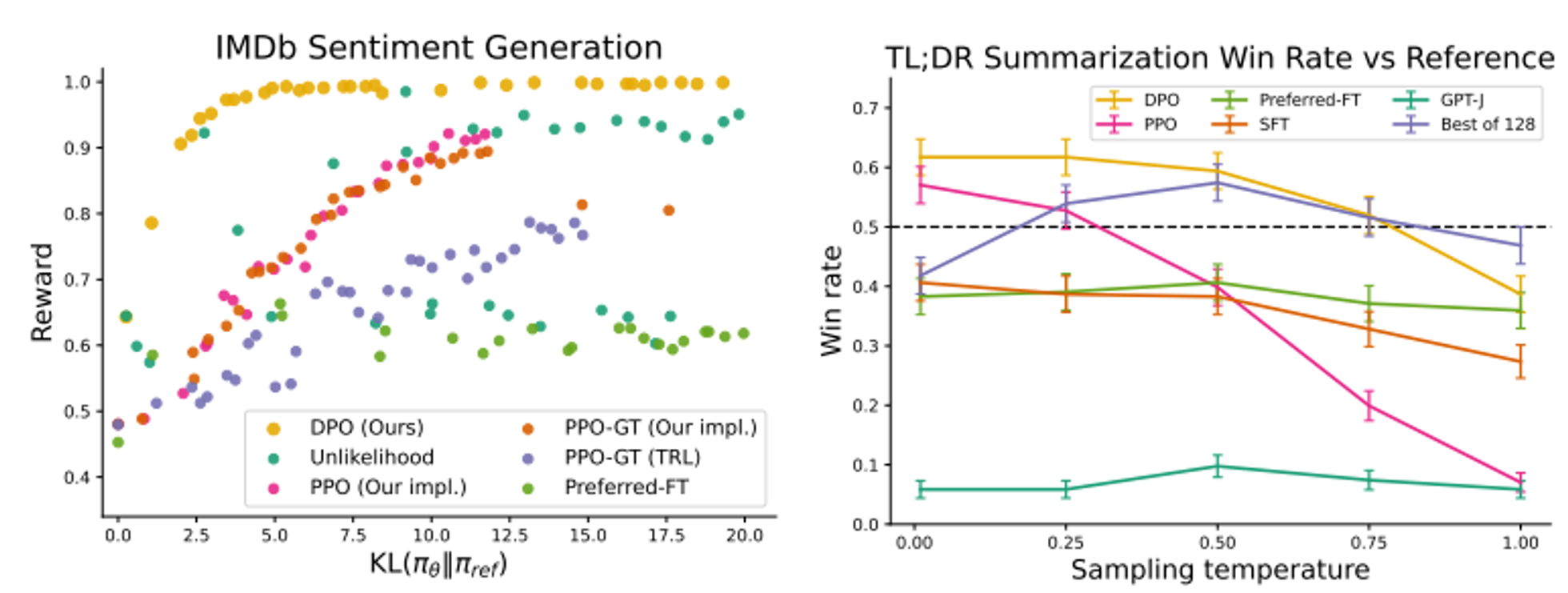
  • 같은 데이터로 DPO reward는 PPO reward보다 높게 계산되며, sampling temperature가 높은 상황에서도 높은 win rate를 가져갈 수 있음

IPO (Identity Preference Optimization, Deepmind 2023)

A General Theoretical Paradigm to Understand Learning from Human...

• 근본적으로 RLHF의 reward model인 Bradley-Terry 모델이 문제를 가지고 있다고 함
  $\mathcal{L}_R=-\mathbb{E}_{(x,y_w,y_l)\sim D}[\log\sigma(r_\phi(x,y_w)-r_\phi(x,y_l))]$
  • 위 loss로 모델이 완전히 학습되는 경우 $r(y_w)-r(y_l)\rightarrow+\infin$을 만족해야 함
  • 즉, $\pi(y_w)=1$, $\pi(y_l)=0$이 되어야 함
  • 이때 RLHF는 KL-divergence를 regularizer로 사용하는데, 저 확률 분포는 완전한 one-hot distribution이기 때문에, KL-divergence가 $+\infin$로 발산하게 됨
  • 따라서, Bradley-Terry 모델 기반의 reward model은 필연적으로 underfit되어야 함
• 그러나, DPO의 경우 이를 제어할 수 있는 수단이 없음
  • Bradley-Terry 모델을 사용하면서, KL-divergence와 같은 regularizer가 존재하지 않음
  • 때문에 IPO에서는 기존 sigmoid 기반 loss function 대신 MSE 기반의 loss function을 적용하여 해결
• IPO loss function
  $\mathcal{L}_\text{IPO}(\pi_\theta;\pi_\text{ref})=\mathbb{E}_{(x,y_w,y_l)\sim D}[(\log\frac{\pi_\theta(y_w|x)}{\pi_\theta(y_l|x)}-\log\frac{\pi_\text{ref}(y_w|x)}{\pi_\text{ref}(y_l|x)}-\frac{1}{2\beta})^2]$
  • 위 방법론의 기본적 원리 또한 (1) $y_w$의 likelihood 증가, (2) $y_l$의 likelihood 감소인 점은 동일
  • 대신 그 차이가 reference sample 간 likelihood 차이와 $\frac{1}{2\beta}$의 합 만큼만 날 정도로, 너무 커지지 않게 regularize하는 term을 넣어주었다고 보면 됨
• 실험 결과
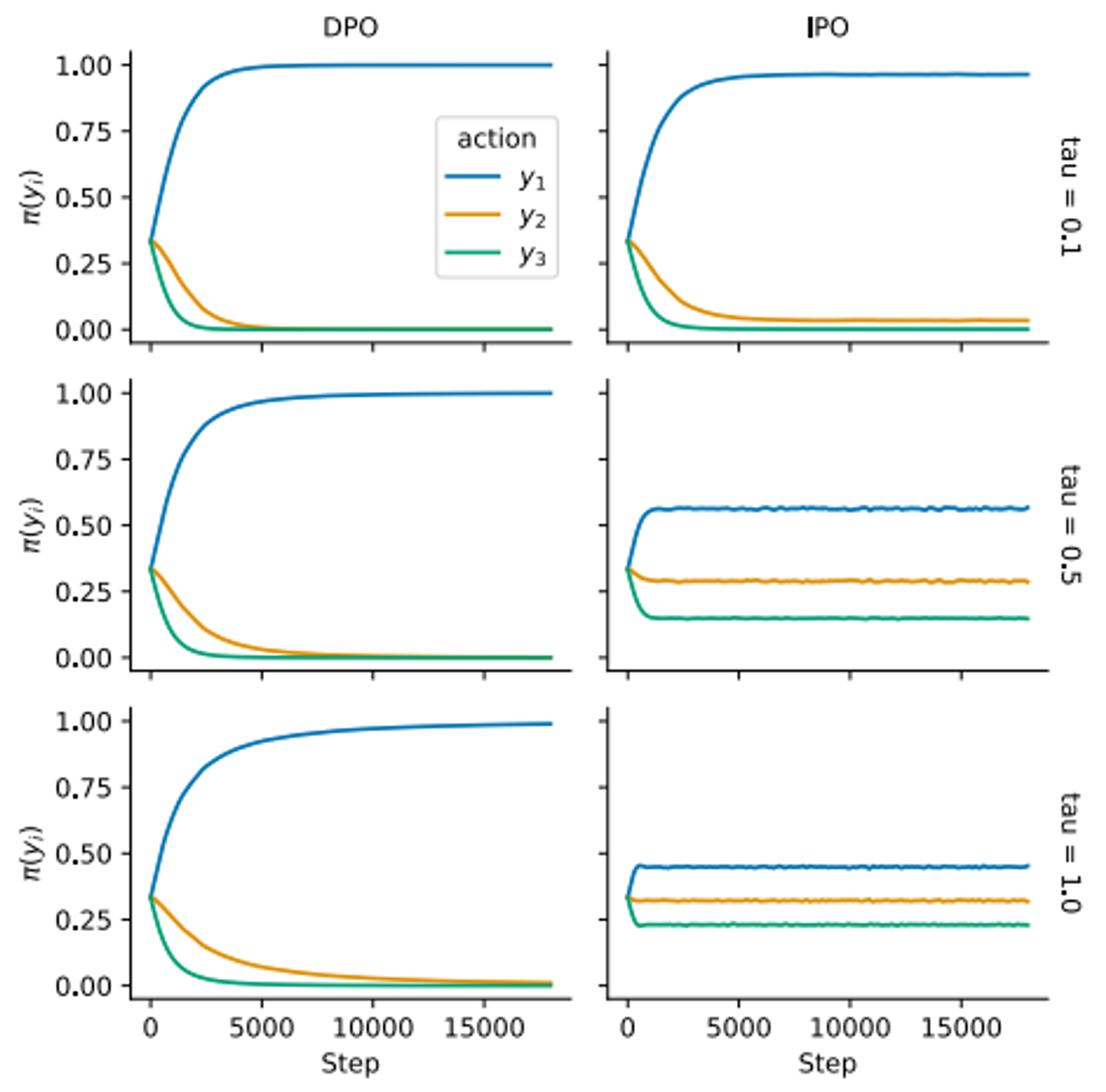
  • $y_1>y_2>y_3$ 순서의 preference를 가진 데이터에 대한 training curve
  • DPO는 $\tau$ 값에 관계 없이 $y_1$에 대한 생성 확률만 극대화하고, $y_2$와 $y_3$의 생성 확률은 0에 수렴하도록 학습됨
  • 그러나 IPO는 greedy policy로 인해 과적합되는 것을 피하며, $y_2$, $y_3$도 때에 따라 생성할 수 있는 여지를 남겨둠($\pi(y_2),\pi(y_3)\gg0$)
  • 즉, annotation error로 인한 과적합을 적절한 sampling 방식으로 해소할 수 있다는 것

RRHF (Rank Responses Alignment, Alibaba 2023)

RRHF: Rank Responses to Align Language Models with Human Feedback...

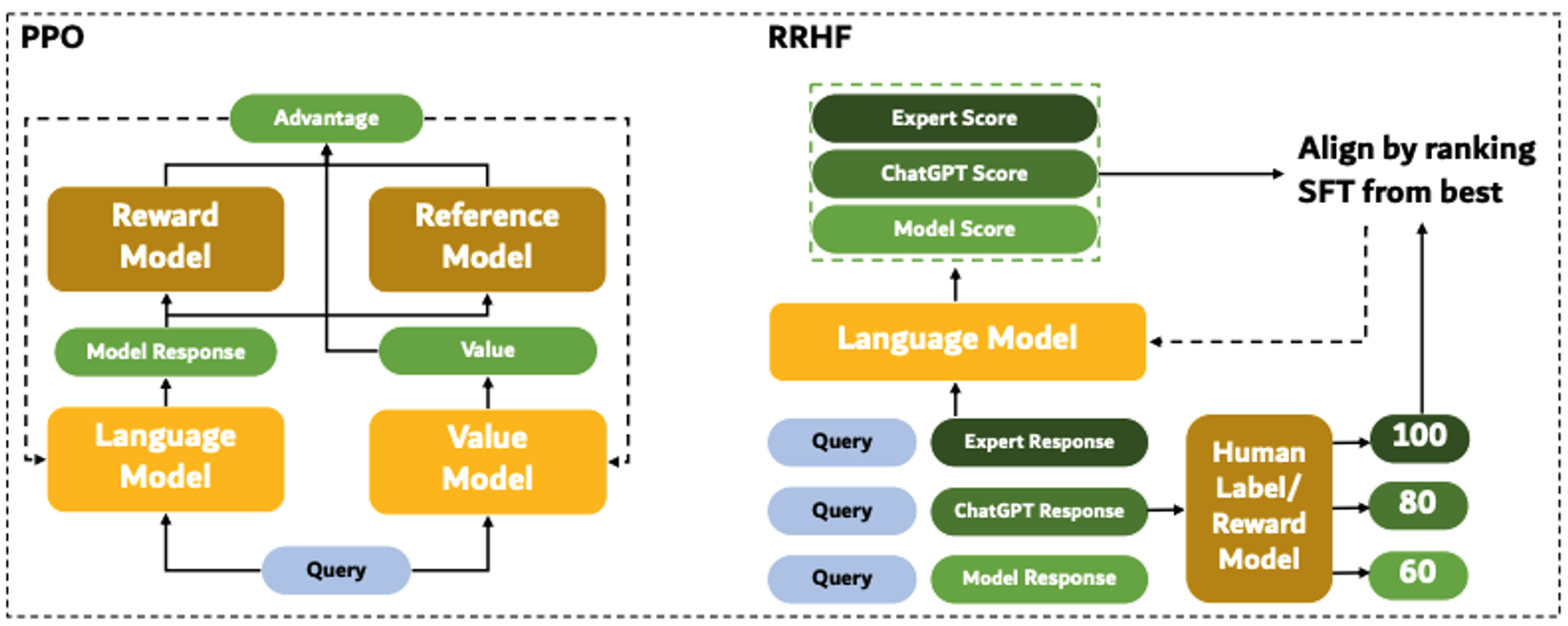
• Chosen-Rejected pair 데이터가 아닌, 다수의 response에 대한 ranking을 사용함
  • 사실 OpenAI GPT-3.5의 RLHF도 pair가 아닌 ranking을 사용하긴 했지만, 보통 annotation 난이도를 이유로 오픈 소스 데이터들은 대부분 pair로 구성됨
• RRHF loss function (preference optimization)
  $L_\text{rank}=\sum_{r_i<r_j}\max(0,p_i-p_j) ,\quad p_i=\frac{\sum_t\log P_\pi(y_{i,t}|x,y_{i,<t})}{||y_i||}$
  • 단순하게 보면, high-rank 샘플의 likelihood가 low-rank 샘플의 likelihood보다 높아지게 하는 함수
  • Pair 데이터라 생각한다면, SLiC-HF의 hinge loss에서 margin을 사용하지 않는 것과 동일함
• RRHF loss function (SFT)
  $L_\text{SFT}=-\sum_t\log P_\pi(y_{i',t}|x,y_{i',<t})$
  • 모은 데이터들 중 highest-rank인 데이터에 대해서만 SFT loss를 적용해줌
  • Preference optimization에만 사용하기엔 아깝기도 하고, 원래 rejection-sampling이라는 방법론의 일종이기도 함
  • 최종 loss는 $L=L_\text{rank}+L_\text{SFT}$
• 실험 결과
  • RRHF로 학습된 모델을 이용해 데이터를 다시 생성하고 그에 ranking을 부여해 한 번 더 RRHF iteration을 돌리는 경우, single iter 모델보다 성능이 좋아짐
  • 다만 학습 모델만을 이용해 너무 많은 iteration을 수행하게 되면, reward는 증가하나 실제 PPL와 win rate가 감소하는 ‘reward hacking’이 발생할 수 있다고 함