6장 - 게이트가 추가된 RNN

앞에서 본 RNN은 과거의 정보를 기억할 수 있었다. 구조가 단순해서 구현도 쉽지만, 안타깝게도 성능이 좋지 못하다. 그 원인은 대부분의 경우 시계열 데이터에서 시간적으로 멀리 떨어진, 장기(long term) 의존 관계를 잘 학습할 수 없다는 데 있다.

요즘은 단순한 RNN 대신 LSTM이나 GRU라는 계층이 주로 쓰인다. LSTM이나 GRU에는 게이트$^{gate}$라는 구조가 더해져 있는데, 이 덕분에 시계열 데이터의 장기 의존 관계를 학습할 수 있다.

6.1 - RNN의 문제점

기본적인 RNN은 시계열 데이터의 장기 의존 관계를 학습하기 어렵다. 그 원인은 BPTT에서 기울기 소실 혹은 기울기 폭발이 일어나기 때문이다.

• 기울기 소실: 역전파 값이 점점 작아지다가 0이 되어 사라지는 현상
• 기울기 폭발: 역전파의 값이 매우 큰 수가 되는 현상

6.1.1 - RNN 복습

RNN 계층은 시계열 데이터인 $\bold x_t$를 입력하면 $\bold h_t$를 출력한다. 이 $\bold h_t$가 은닉 상태 벡터라고 하여, 과거 정보를 저장한다.

RNN은 이 은닉 상태 벡터를 이용하여 과거 정보를 계승한다.

6.1.2 - 기울기 소실 또는 기울기 폭발

앞 장에서 RNN을 사용한 언어 모델을 RNNLM이라 했다. 이번 절에서는 RNNLM의 단점을 확인하는 차원에서 다음 문제를 다시 한 번 생각해 보자.

"?"에 들어가는 단어는 "Tom"이다. 이 문제에 답하기 위해서는 앞 문장의 정보들을 은닉 상태 벡터에 인코딩해 보관해둬야 한다.

RNNLM의 역전파는 BPTT로 수행된다. 정답 레이블이 "Tom"이라고 주어진 시점으로부터 과거 방향으로 기울기가 전달된다.

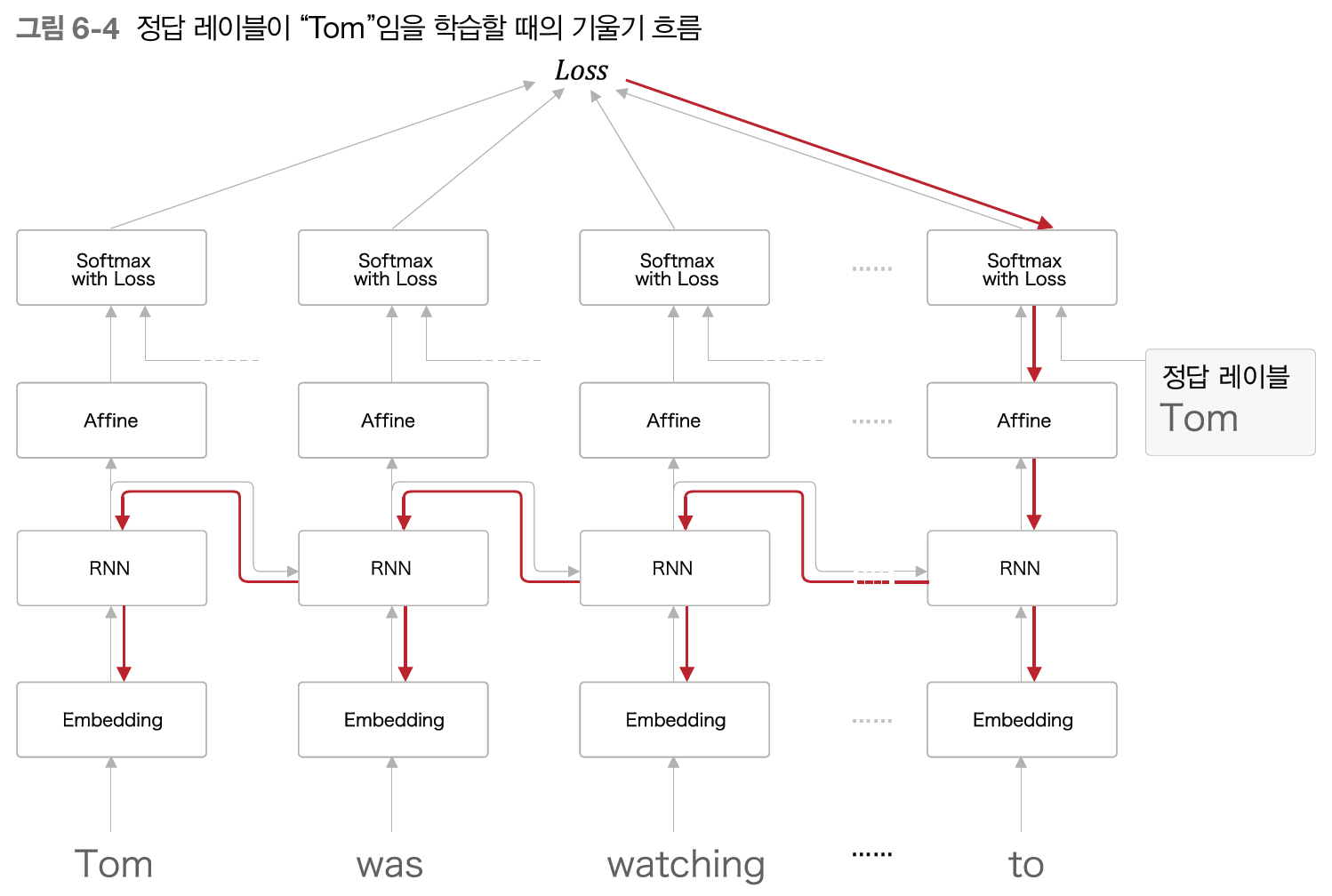
원래대로라면 RNN 계층이 과거 방향으로 '의미 있는 기울기'를 전달함으로써 시간 방향의 의존 관계를 학습할 수 있어야 한다.

하지만 이 기울기가 중간에 사그라들면, 즉 정보가 거의 남지 않게 되면 가중치 매개변수는 갱신되지 않는다. 기울기 폭발도 마찬가지이다.

6.1.3 - 기울기 소실과 기울기 폭발의 원인

원인을 파악하기 위해 RNN 계층에서의 시간 방향 역전파, 즉 은닉 상태 벡터의 기울기 흐름에 주목해 보자.

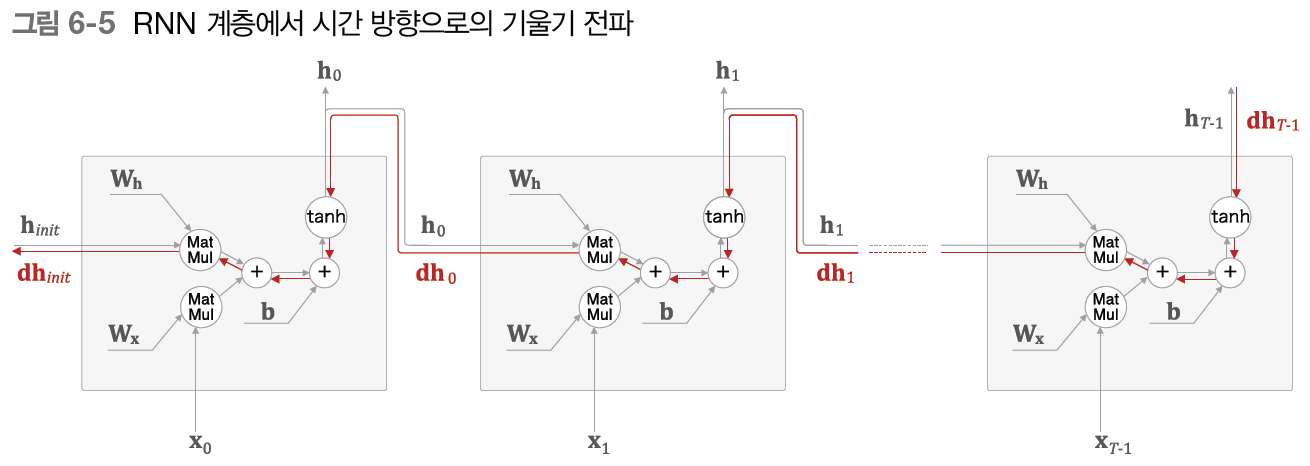
길이가 $T$인 시계열 데이터를 가정했다. 시간 방향 기울기에 주목하면 역전파로 전해지는 기울기는 차례로
'$\tanh$', '$+$', 행렬곱 연산을 통과한다는 것을 알 수 있다.

'$+$'의 역전파는 상류에서의 기울기를 그대로 흘릴 뿐이므로 기울기에 변화가 없다. 그럼 나머지 두 연산을 살펴보자.

우선 '$\tanh$'를 살펴보자. $y=\tanh (x)$일 때의 미분은 $\frac{\partial y}{\partial x} = 1-y^2$이다. 이때 $y=\tanh (x)$의 값과 그 미분 값을 각각 그래프로 그리면 다음과 같다.

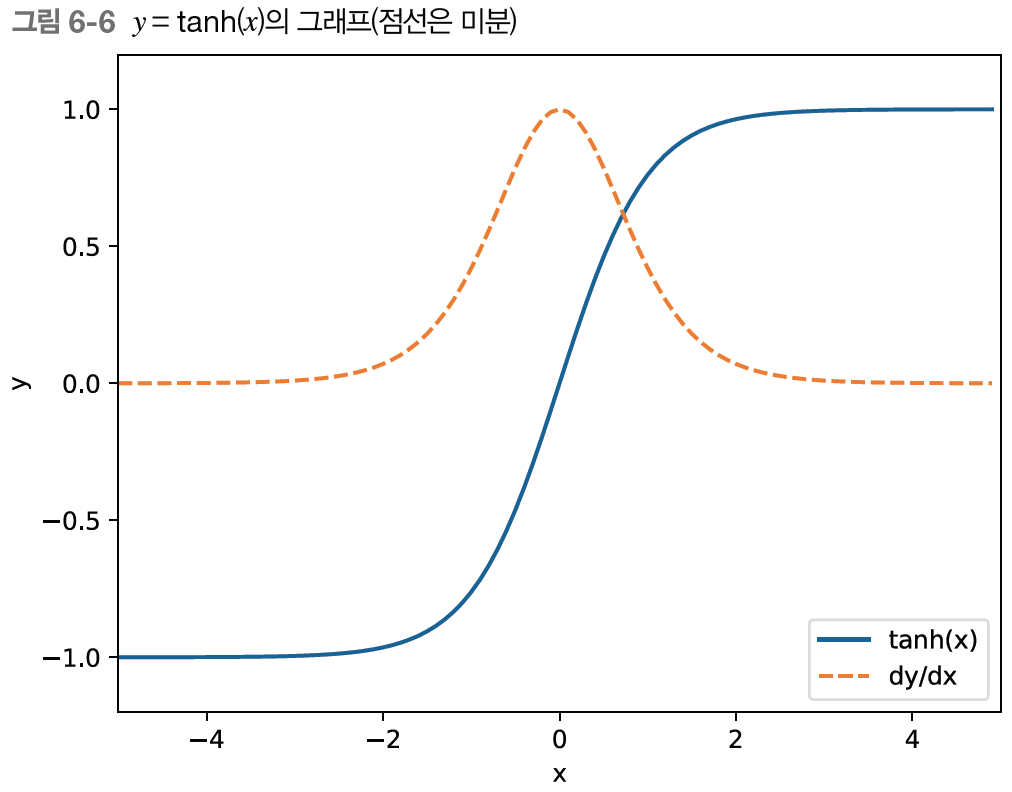
미분을 보면 그 값이 항상 1.0 이하이고 $x$가 0으로부터 멀어질수록 작아진다. 그리고 역전파는 이전에 흘러들어온 기울기에 이 값을 곱하기 때문에, 기울기가 점점 작아지게 된다.

$\tanh$ 노드를 지날 때마다 기울기가 작아진다는 것은 확인했다. 그럼 행렬곱 노드는 어떨까? 단순하게 생각하기 위해서 잠깐 $\tanh$ 노드를 무시하고 생각해 보자.

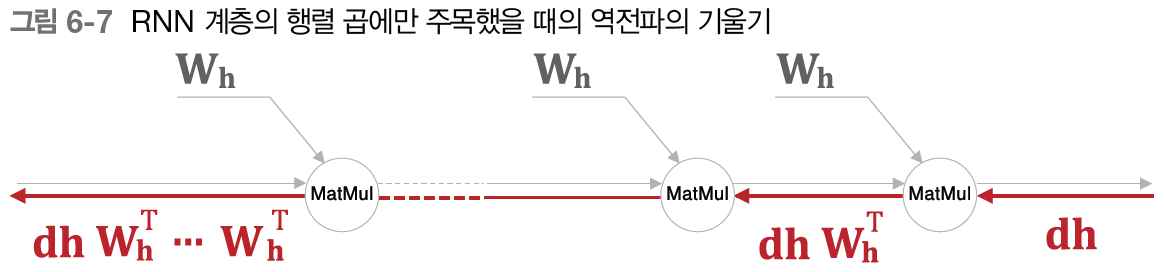
$T$의 시간부터 흘러온 역전파가 $L$일 때 $\frac{\partial L}{\partial \bold h_t}= \frac{\partial L}{\partial \bold h_{t+1}} \bold W_{\bold h}^T$가 된다. 위의 그림에서 생각하면 위로부터 흘러온 기울기 $\bold d \bold h$에 $\bold W_{\bold h}^T$를 계속해서 곱하는 것이다. 여기에서 주목할 점은 이 행렬 곱셈에서는 매번 똑같은 가중치인 $\bold W_{\bold h}$가 사용된다는 것이다.

이런 식으로 역전파가 이루어지면 결과는 대부분 다음 두 경우 중 하나이다.

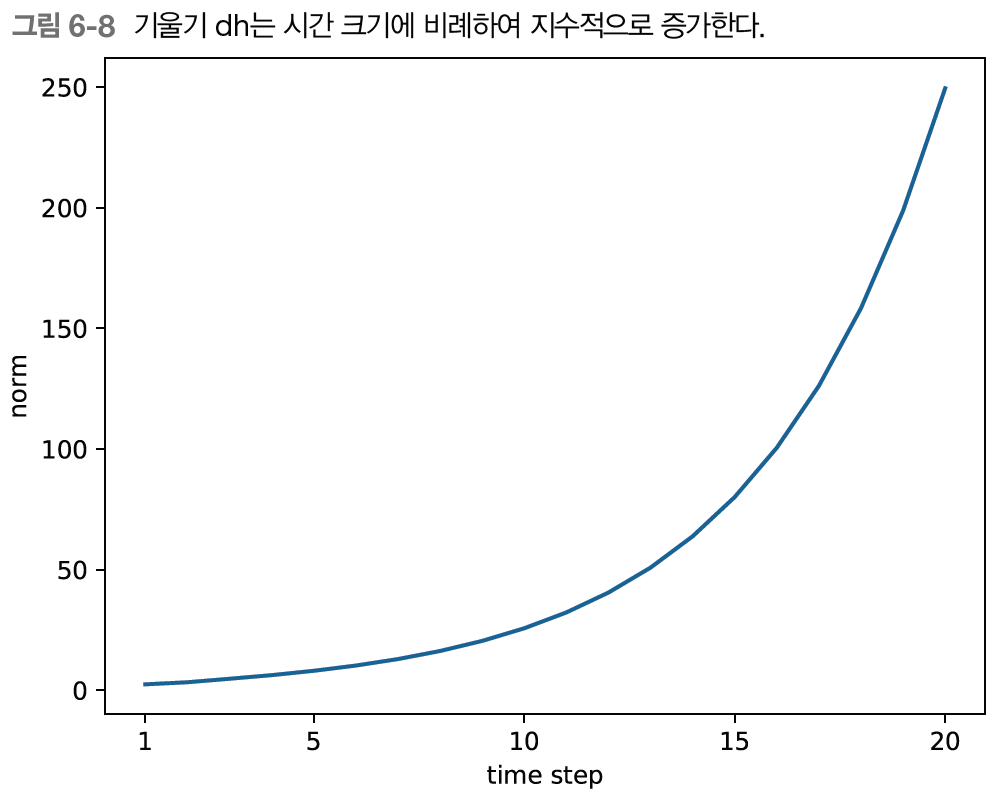
기울기가 시간에 비례해 지수적으로 증가하는 경우. 기울기 폭발$^{exploding \space gradients}$이다. 기울기 폭발이 일어나면 오버플로를 일으켜 NaN 같은 값을 발생시킨다.

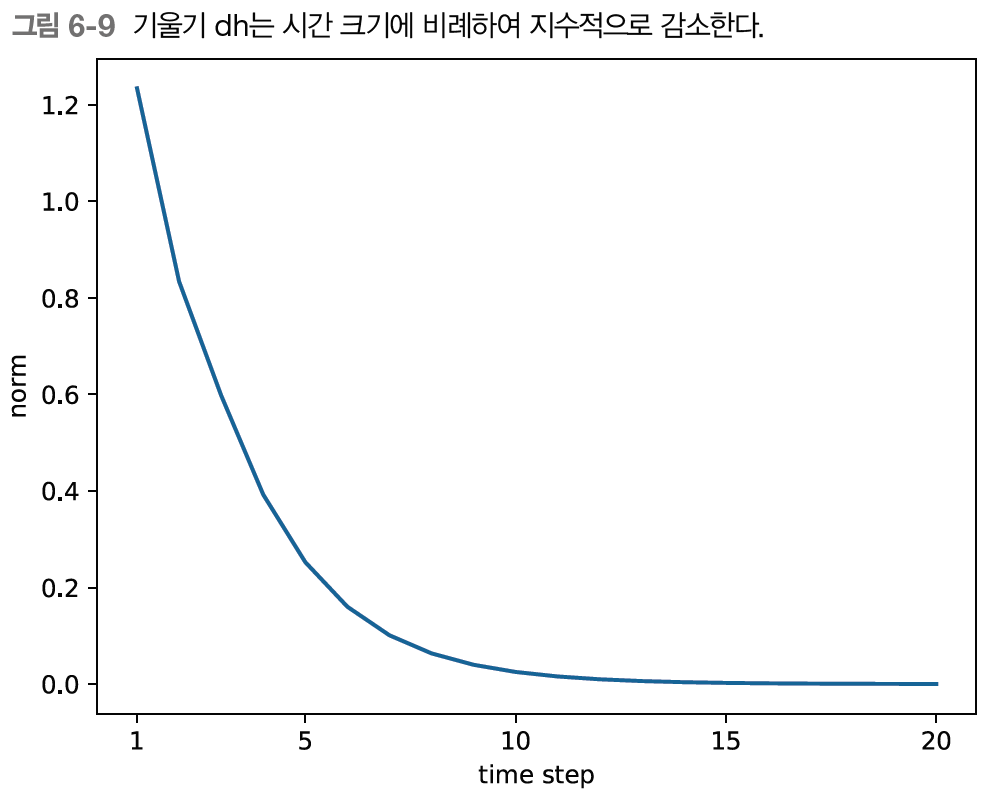
이번에는 기울기가 지수적으로 감소한다. 이게 기울기 소실$^{vanishing \space gradients}$이다. 기울기가 일정 수준 이하로 작아지면 가중치 매개변수가 더 이상 갱신되지 않으므로 장기 의존 관계를 학습할 수 없게 된다.

왜 이런 지수적인 변화가 나타날까? 간단하게 생각하면 $\bold W_{\bold h}^T$를 반복해서 곱했기 때문이다. 이걸 스칼라라고 생각하면 이야기는 단순해진다. 값이 1보다 크면 지수적으로 증가하고, 값이 1보다 작으면 지수적으로 감소한다.

근데 스칼라가 아니라 행렬로 생각하는 경우, 행렬의 '특잇값'이 척도가 된다. 행렬의 특잇값이란 간단히 말하면 데이터가 얼마나 퍼져 있는지를 나타낸다. 여러 특잇값 중 최댓값이 1보다 큰지 여부를 보면 기울기 크기가 어떻게 변할지 예측할 수 있다.

WARNING_ 특잇값의 최댓값으로 가능성을 예측할 수는 있으나, 1보다 크다고 해서 무조건 기울기가 폭발하는 것은 아니다. 어디까지나 가능성을 예측할 수 있다는 것이다.

6.1.4 - 기울기 폭발 대책

기울기 폭발의 대책으로는 전통적인 기법, 기울기 클리핑$^{gradients \space cipping}$이 있다. 그 알고리즘을 의사 코드로 쓰면 다음과 같다.

신경망에서 사용되는 모든 매개변수에 대한 기울기를 하나로 처리한다고 가정하고, 이를 기호 $\hat \bold g$으로 표기했다. 그리고 $threshold$를 문턱값으로 설정한다.

이때 $|| \hat \bold g||$(기울기의 L2 노름)이 문턱값을 초과하면 기울기를 수정한다. $|| \hat \bold g||$가 $threshold$에 비해 커질수록 기울기가 많이 줄어든다. 단순한 알고리즘이지만, 많은 경우에 잘 작동한다.

WARNING_ $\hat \bold g$은 신경망에서 사용되는 모든 매개변수의 기울기를 하나로 모은 것이다. 만약 W1과 W2 매개변수를 사용하는 모델이 있다면 dW1과 dW2를 결합한 것을 $\hat \bold g$이라 한다.

6.2 - 기울기 소실과 LSTM

기울기 소실을 해결하려면 RNN 계층의 아키텍처를 근본부터 뜯어고쳐야 한다. 여기서 등장하는 게 바로 게이트이다.

게이트가 추가된 RNN의 대표격이 LSTM(Long Short Term Memory)과 GRU이다.

6.2.1 - LSTM의 입출력

LSTM을 살펴보기 전에 계산 그래프를 단순화하는 도법을 하나 도입하자.

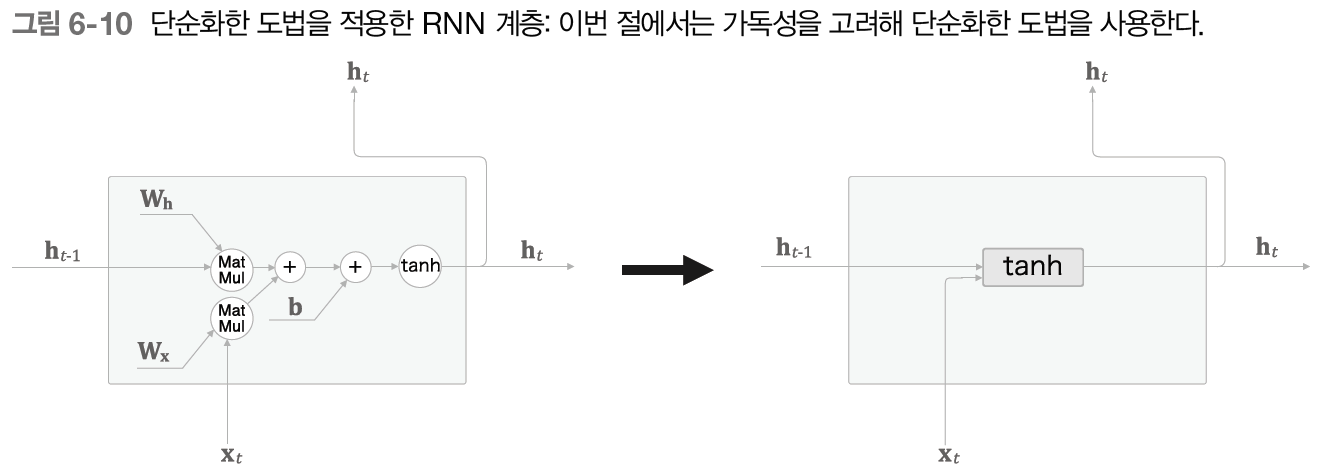
$\tanh(\bold h_{t-1} \bold W_{\bold h} + \bold x_t \bold W_{\bold x} + \bold b)$ 계산을 $\tanh$라는 직사각형 노드 하나로 그리자.

이제 LSTM의 입출력을 RNN과 비교하는 것부터 시작해보자.

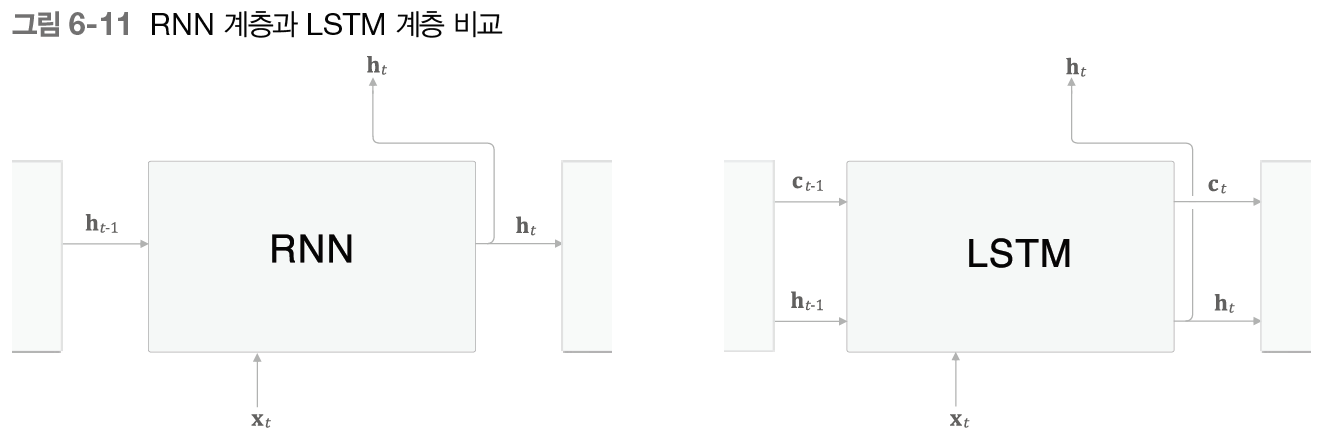
LSTM 계층의 입출력에는 $\bold c$라는 경로가 있다는 차이가 있다. 이 $\bold c$를 기억 셀$^{memory \space cell}$, 혹은 단순히 '셀'이라고 하기도 한다. 이게 바로 LSTM 전용의 기억 메커니즘이다.

기억 셀의 특징은 LSTM 계층 내에서만 주고받으며 다른 계층으로는 출력하지 않는다는 것이다. 반면, 은닉 상태 벡터 $\bold h$는 RNN 계층과 마찬가지로 다른 계층으로 출력된다.

NOTE_ 외부에서는 기억 셀이 보이지 않으므로 그 존재를 생각할 필요가 없다.

6.2.2 - LSTM 계층 조립하기

LSTM에는 기억 셀 $\bold c_t$가 있다. 이 $\bold c_t$에는 시각 $t$에서의 LSTM의 기억이 저장돼 있는데, 과거로부터 시각 $t$까지에 필요한 모든 정보가 저장돼 있다고 가정한다.

필요한 정보를 모두 간직한 이 정보를 바탕으로 은닉 상태 벡터 $\bold h_t$를 출력한다.

• 이때 출력하는 $\bold h_t$는 기억 셀을 $\tanh$ 함수로 변환한 값이다. 앞에서 말한 단순화가 아니라 진짜 변환만 하면 된다.

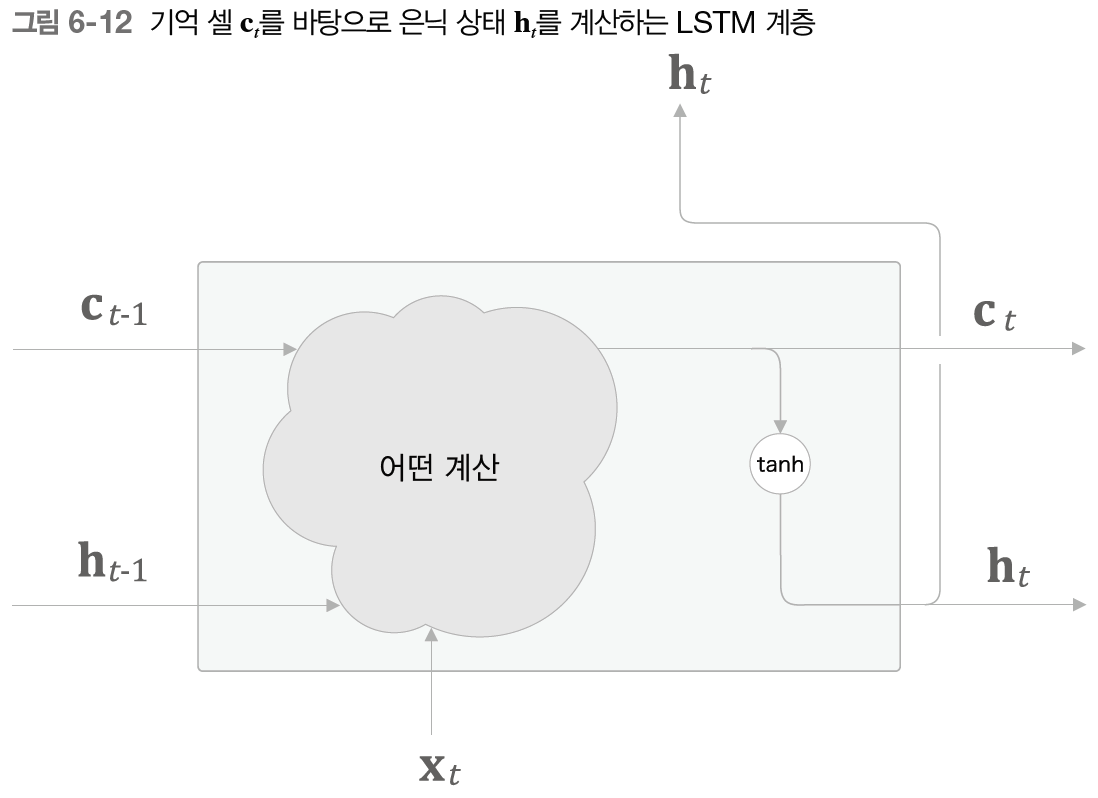
원래는 은닉 상태 벡터를 $\bold h_t=\tanh(\bold h_{t-1} \bold W_{\bold h} + \bold x_t \bold W_{\bold x} + \bold b)$로 직접 계산했지만, 이제는 기억 셀을 바탕으로 변환만 하면 된다.

물론 $\tanh$ 변환은 기억 셀 원소 각각에 적용해야 한다. $\bold c_t$와 $\bold h_t$의 원소 수는 같아야 한다.

이쯤에서 '게이트'라는 기능에 대해 알아보자. 문을 열거나 닫을 수 있듯이, 게이트는 데이터의 흐름을 제어한다.

LSTM에서 사용하는 게이트는 열고 닫는 것뿐만 아니라 다음 단계로 흘려보낼 물의 양을 조절할 수 있다. 흘려보내는 양을 열림 상태$^{openness}$라 부른다.

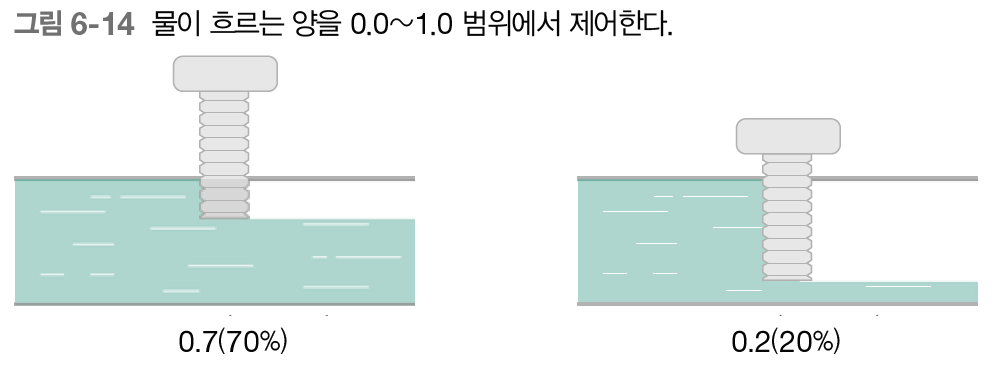
게이트의 열림 상태는 0에서 1 사이의 실수로 나타난다. 여기서 중요한 것은 게이트의 열림 상태도 데이터로부터 자동으로 학습한다는 점이다.

NOTE_ 게이트의 열림 상태를 제어하기 위해서 전용 가중치 매개변수를 이용한다. 참고로, 게이트의 열림 상태를 구할 때는 시그모이드 함수를 사용하는데, 시그모이드 함수의 출력이 0과 1 사이의 실수이기 때문이다.

6.2.3 - output 게이트

앞에서 은닉 상태 벡터 $\bold h_t$는 기억 셀 $\bold c_t$에 단순히 $\tanh$ 함수를 적용했을 뿐이라고 얘기했다. 다만 이번에는 $\tanh(\bold c_t)=\bold h_t$는 아니다. 그 전에 게이트를 적용할 것이다.

이번 절에서는 게이트의 적용에 대해 생각해 보자. 즉, $\tanh(\bold c_t)$의 각 원소에 대해 그것이 다음 시각의 은닉 상태에 얼마나 중요한지를 조정한다.

한편, 이 게이트는 다음 은닉 상태 벡터의 출력을 담당하는 게이트이므로 output 게이트(출력 게이트)라고 한다.

output 게이트의 열림 상태는 입력 $\bold x_t$와 이전 상태 $\bold h_{t-1}$로부터 구한다. 이때 계산은 다음과 같다.

여기서 사용하는 가중치 매개변수와 편향에는 output의 첫 글자인 $\bold o$를 첨자로 추가한다. 한편, 시그모이드 함수는 $\sigma()$로 표기한다.

시그모이드 함수 내부의 계산은 RNN 계층에서 본 적이 있다. 물론 가중치는 완전히 다르겠지만. 이 계산을 아핀 변환이라고 한다.

• 아핀 변환이란 행렬 변환과 평행 이동(편향)을 결합한 형태를 말한다. 여기서는
  $\bold x_t \bold W_{\bold x}^{(\bold o)} + \bold h_{t-1} \bold W_{\bold h}^{(\bold o)} + \bold b^{(\bold o)}$이 아핀 변환에 해당된다.

이 $\bold o$가 바로 열림 상태이다. 이 $\bold o$와 $\tanh(\bold c_t)$의 원소별 곱을 $\bold h_t$로서 출력하는 것이다. 이상의 계산을 계산 그래프로 그리면 다음과 같다.

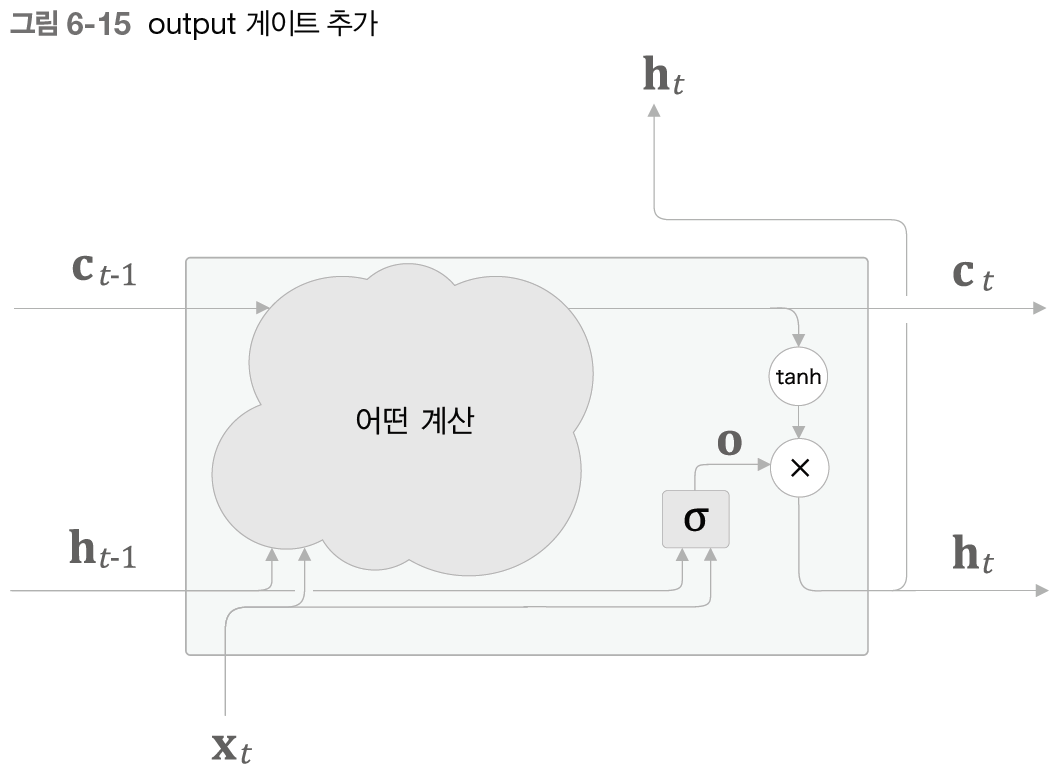
위의 $\sigma$는 단순히 시그모이드 함수가 아니라 output 게이트에서 수행하는 모든 계산을 합친 것이다. 그리고 $\sigma$의 출력인 $\bold o$와 $\tanh(\bold c_{t})$의 곱이 $\bold h_t$이다. 여기서 말하는 곱은 원소별 곱이고, 이것을
아다마르 곱$^{Hadamard \space product}$이라고도 한다. 기호로는 $\odot$으로 나타내며, 다음과 같은 계산을 수행한다.

WARNING_ $\tanh$의 출력은 -1.0~1.0 사이의 실수이다. 이 수치를 그 안에 인코딩된 '정보'의 강약(정도)을 표시한다고 해석할 수 있다. 따라서 실질적인 '정보'를 지니는 데이터에는 주로 $\tanh$ 함수가 활성화 함수로 사용된다.

6.2.4 - forget 게이트

망각은 더 나은 전진을 낳는다. 우리가 다음에 해야 할 일은 기억 셀에 '무엇을 잊을까'를 명확하게 지시하는 것이다. 이런 일도 게이트를 사용해 해결한다.

위 역할을 하는 게이트를 forget 게이트(망각 게이트)라고 하자. forget 게이트를 LSTM 계층에 추가하면 계산 그래프는 다음과 같다.

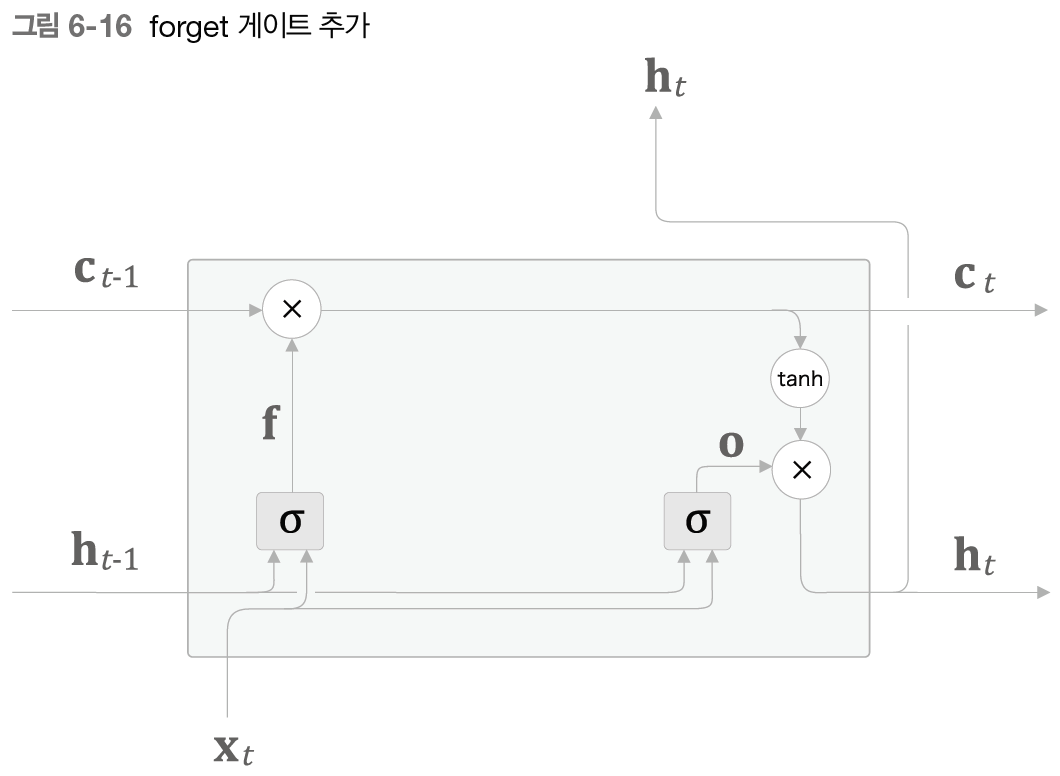
forget 게이트가 수행하는 일련의 계산을 $\sigma$ 노드로 표기했다. 이 $\sigma$ 안에는 forget 게이트 전용의 가중치 매개변수가 있다.

형태는 RNN 계층의 수식이나 output 게이트와 (첨자 빼고) 같지만, 가중치 매개변수가 다르기 때문에 같은 형태의 식이더라도 각자의 역할을 수행할 수 있다.

위 식을 통해 $\bold f$를 구하고 이전 기억 셀인 $\bold c_{t-1}$과의 원소별 곱을 계산해 주면 된다.

6.2.5 - 새로운 기억 셀

forget 게이트를 거치면서 이전 시각의 기억 셀로부터 잊어야 할 기억이 삭제되었다. 그런데 정작 기억을 삭제는 하는데 추가한 적이 없다. 왜 추가한 적이 없냐고?

RNN 계층에서는 은닉 상태 벡터를 계산하면서 기억이 쌓였다. 그런데 이번에는 기억 셀을 계산할 때 forget 게이트밖에 넣은 게 없다는 게 문제다. 그래서 지금 추가하려 한다.

새로 기억해야 할 정보를 기억 셀에 추가하기 위해 다음과 같이 $\tanh$ 노드를 추가한다.

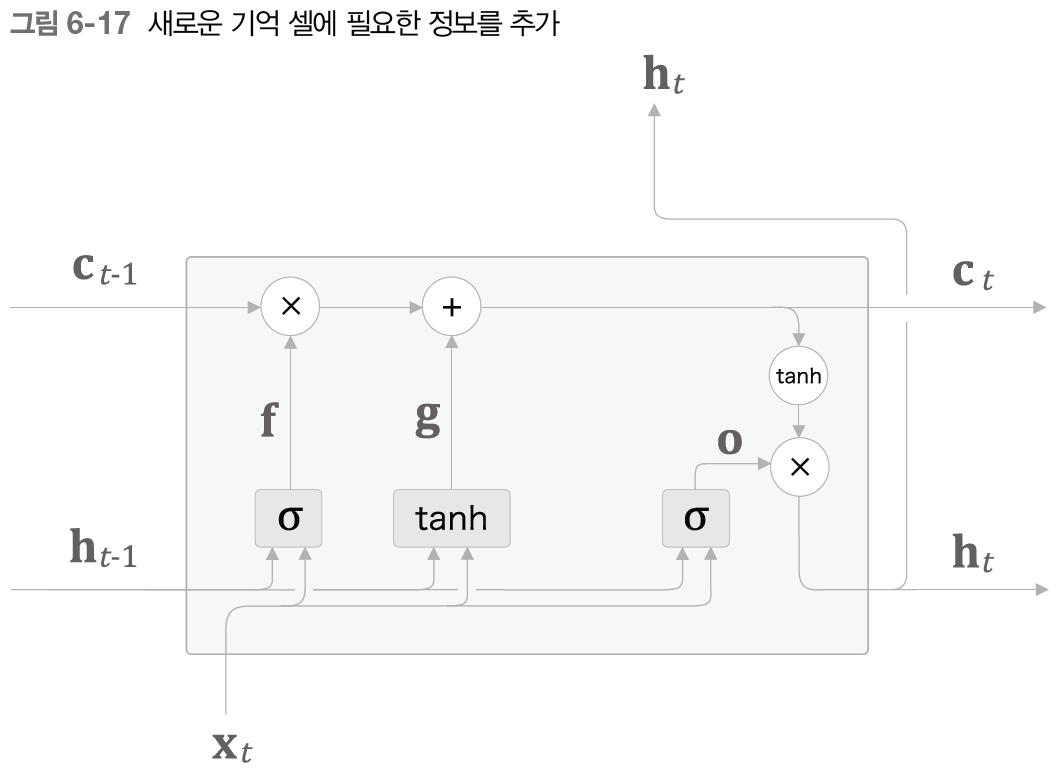
위 그림에서 볼 수 있듯 $\tanh$ 노드를 통과한 결과가 이전 시각의 기억 셀 $\bold c_{t-1}$에 더해진다. 기억 셀에 새로운 '정보'가 추가된 것이다.

이 $\tanh$ 노드는 게이트가 아니고, 새로운 '정보'를 기억 셀에 추가하는 게 목적이다. 따라서 활성화 함수로는 시그모이드 함수가 아니라 $\tanh$ 함수를 사용한다. 위에서 말했듯 '정보'를 지니는 데이터에는 주로 $\tanh$ 함수가 활성화 함수로 사용된다.

이 $\tanh$ 노드에서 수행하는 계산은 다음과 같다.

기억 셀에 추가하는 새로운 기억을 $\bold g$로 표기했다. 이 $\bold g$가 이전 시각의 기억 셀에 더해짐으로써 새로운 기억이 생겨난다.

6.2.6 - input 게이트

마지막으로 새로운 기억인 $\bold g$에 게이트를 하나 추가하고자 한다. 이 게이트를 input 게이트라 하겠다. input 게이트를 추가한 그림은 다음과 같다.

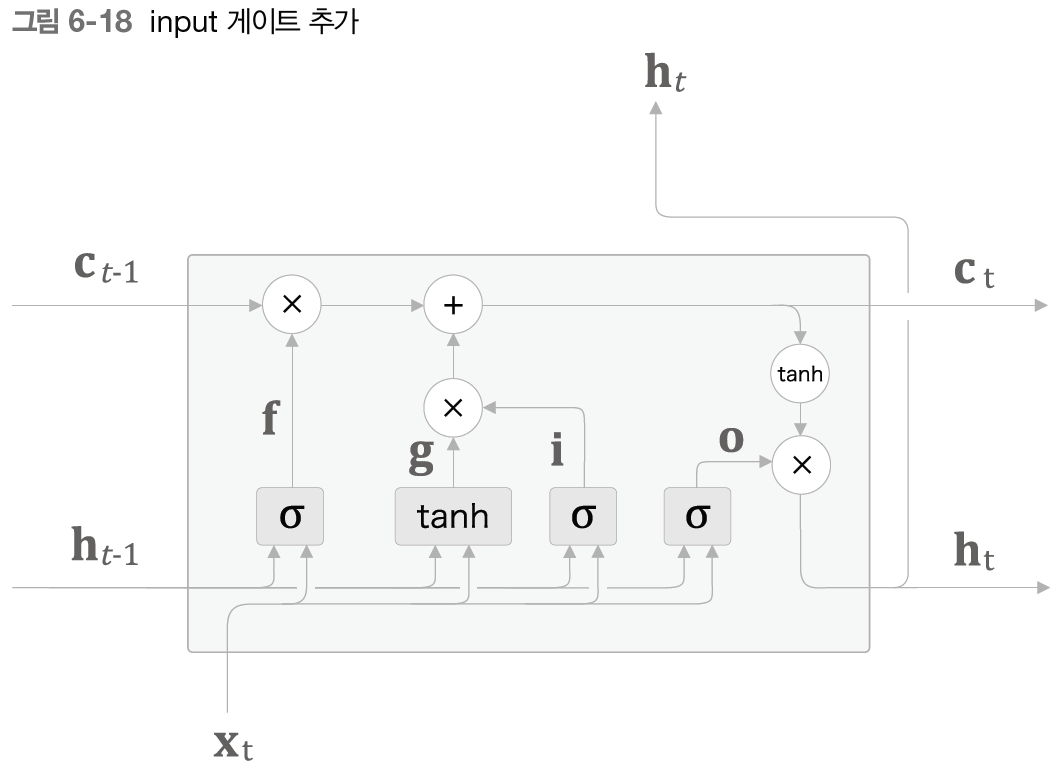
input 게이트는 $\bold g$의 각 원소가 새로 추가되는 정보로서의 가치가 얼마나 큰지를 판단한다. 새 정보를 적절히 취사선택하는 게 이 게이트의 역할이다. 다른 관점에서 보면, 'input 게이트에 의해 가중된 정보'가 새로 추가되는 셈이다.

수행하는 계산은 다음과 같다.

게이트이기 때문에 시그모이드 함수를 활성화 함수로 사용한다.

그런 다음 $\bold i$와 $\bold g$의 원소별 곱 결과를 기억 셀에 추가한다.

6.2.6.5 - LSTM 정리

간단하게 정리하자면 다음과 같다.

• output 게이트는 $\tanh(\bold c_t)$의 각 원소에 대해 그것이 다음 시각의 은닉 상태에 얼마나 중요한지를 조정한다. $\tanh(\bold c_t)$와 원소별 곱을 함으로써 은닉 상태 벡터를 만든다.

• forget 게이트는 기억 셀에 무엇을 잊을지를 명확하게 지시하는 역할을 한다. 이전 시각의 기억 셀과 원소별 곱을 한다.

• 새로운 기억은 기억 셀에 새로운 '정보'를 추가한다. 게이트가 아니므로 $\tanh$ 함수를 사용하며 input 게이트와 원소별 곱을 한 결과를 기억 셀에 더한다.

• input 게이트는 새로운 기억을 만들 때 새로 추가되는 정보로서의 가치를 판단한다. input 게이트와 새로운 기억의 원소별 곱을 한 결과를 기억 셀에 더한다.

6.2.7 - LSTM의 기울기 흐름

LSTM이 어떤 원리로 기울기 소실을 없애주는 걸까? 그 원리는 기억 셀 $\bold c$의 역전파에 주목하면 보인다.

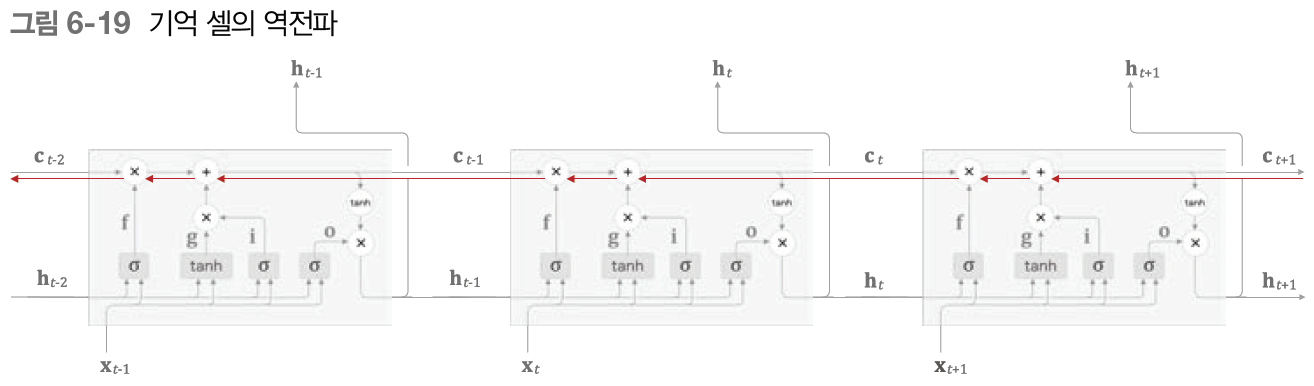
기억 셀의 역전파에 집중해 보면, '$+$' 노드와 '$\times$' 노드만을 지난다. '$+$' 노드는 상류에서 전해지는 기울기를 전달만 하기 때문에 기울기 변화는 일어나지 않는다.

'$\times$' 노드는 행렬 곱이 아니라 원소별 곱(아다마르 곱)을 의미한다. 행렬 곱이 아닌 데다가 매 시각 다른 게이트 값을 이용해 원소별 곱을 계산하기 때문에 곱셈의 효과가 누적되지 않는다. 그래서 기울기 소실이 일어나기 어렵다.

위 그림에서 '$\times$' 노드의 계산은 forget 게이트가 제어한다. forget 게이트가 '잊어야 한다'고 판단한 기억 셀의 원소에 대해서는 그 기울기가 작아지는 것이다. 반대로 '잊어서는 안 된다'고 판단한 원소에 대해서는 기울기가 약화되지 않은 채로 전해진다.

WARNING_ LSTM이 Long Short Term Memory인 이유는 단기 기억$^{short \space term \space memory}$을 긴$^{long}$ 시간 지속할 수 있기 때문이다.

6.3 - LSTM 구현

다음은 LSTM에서 수행하는 계산을 정리한 수식들이다.

순서대로 output 게이트, forget 게이트, 새로운 기억, input 게이트이다.

그리고 기억 셀은 forget 게이트와 이전 시각 기억 셀의 원소별 곱에, 새로운 기억과 input 게이트의 원소별 곱을 더한 것이다.

마지막으로 은닉 상태 벡터는 output 게이트와 기억 셀을 $\tanh$ 함수로 변환한 것의 원소별 곱이다.

여기서 주목할 부분은 아핀 변환($\bold x \bold W_{\bold x} + \bold h \bold W_{\bold h} + \bold b$ 형태의 식)을 포함하는 네 수식이다. 위의 네 가지 수식에서는 아핀 변환을 개별적으로 수행하지만, 이를 하나의 식으로 정리할 수 있다.

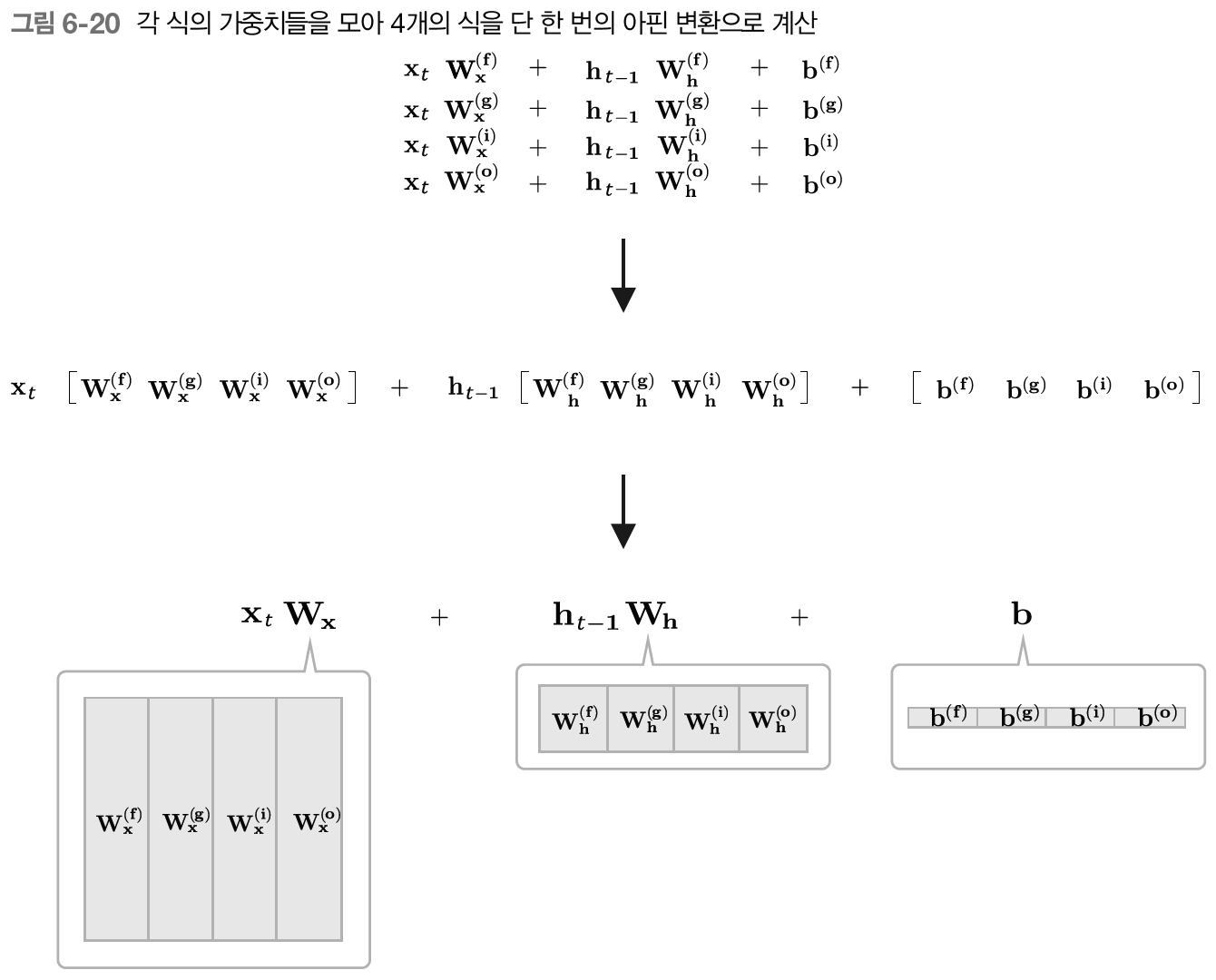
4개의 가중치와 편향을 각각 하나로 모을 수 있고, 이로써 아핀 변환을 단 1번의 계산으로 끝낼 수 있다. 일반적으로 행렬 라이브러리는 '큰 행렬'을 한꺼번에 계산할 때가 각각을 따로 계산할 때보다 빠르기 때문에 계산 속도가 빨라진다는 이점이 있다.

또한, 가중치를 한 데 모아서 관리할 수 있기 때문에 코드 상에서도 간결해진다.

위의 계산을 행렬의 형상으로 보면 다음과 같다.

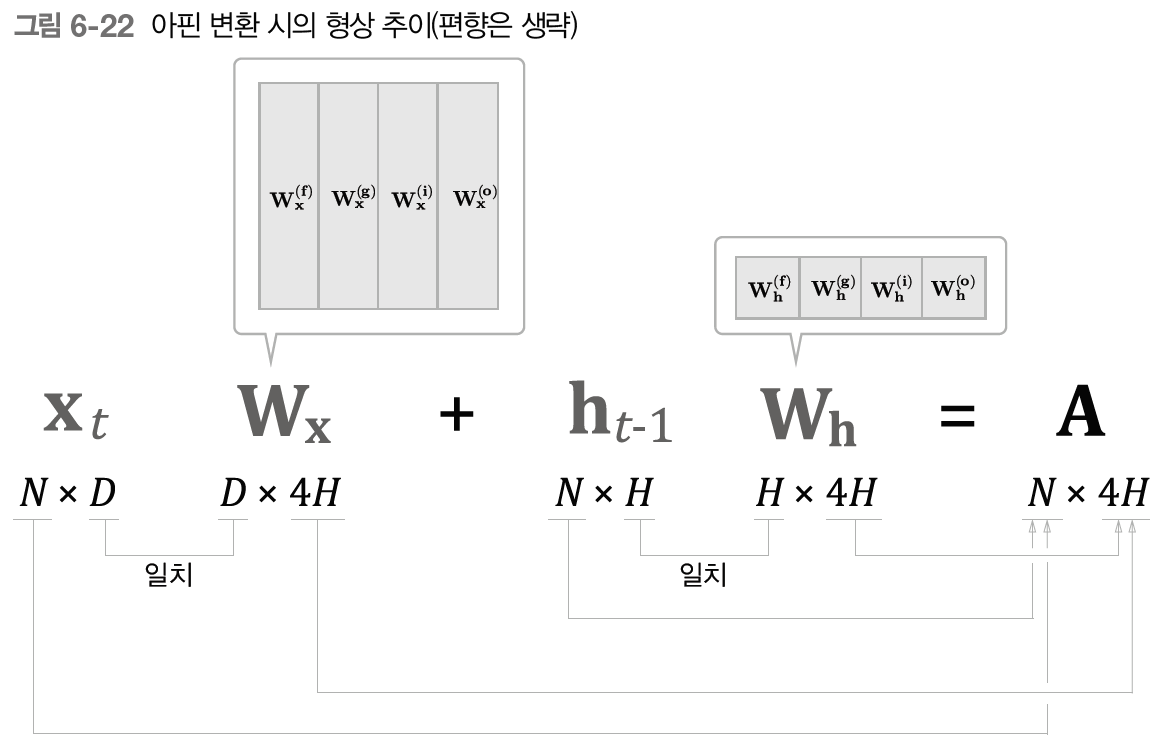
이제 $\bold W_{\bold x}$, $\bold W_{\bold h}$, $\bold b$ 각각에 4개분의 가중치나 편향이 포함되어 있다고 가정하고, 이때의 LSTM을 계산 그래프로 그리면 다음과 같다.

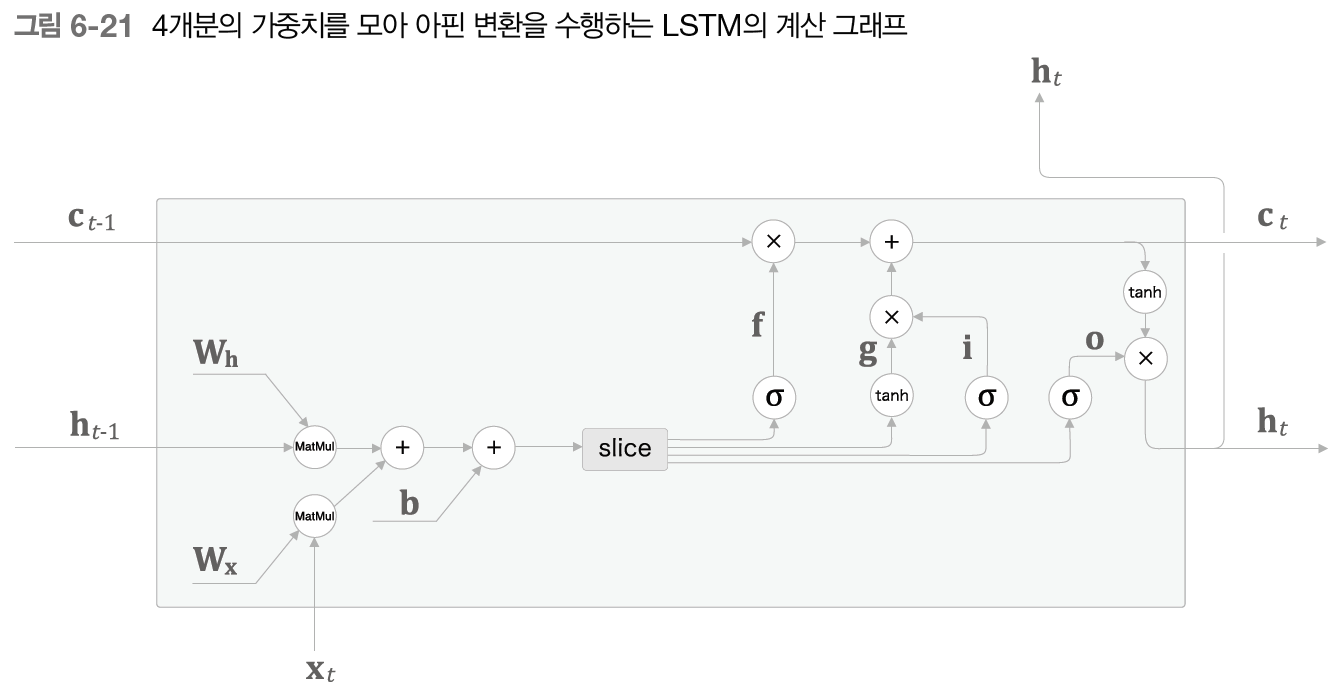
slice는 아핀 변환이 끝난 행렬을 균등하게 네 조각으로 나눠주는 단순한 노드이다. 물론 서로 가중치나 편향이 섞이면 안 된다.

가중치와 편향이 나눠졌다면 각각 알맞은 활성화 함수를 사용해 주면 된다.

slice 노드가 처음 등장했기 때문에 역전파에 대해서 알아봐야 한다. slice 노드는 행렬을 네 조각으로 나눠서 분배했다. 따라서 그 역전파에서는 반대로 4개의 기울기를 하나의 행렬로 결합해야 한다.

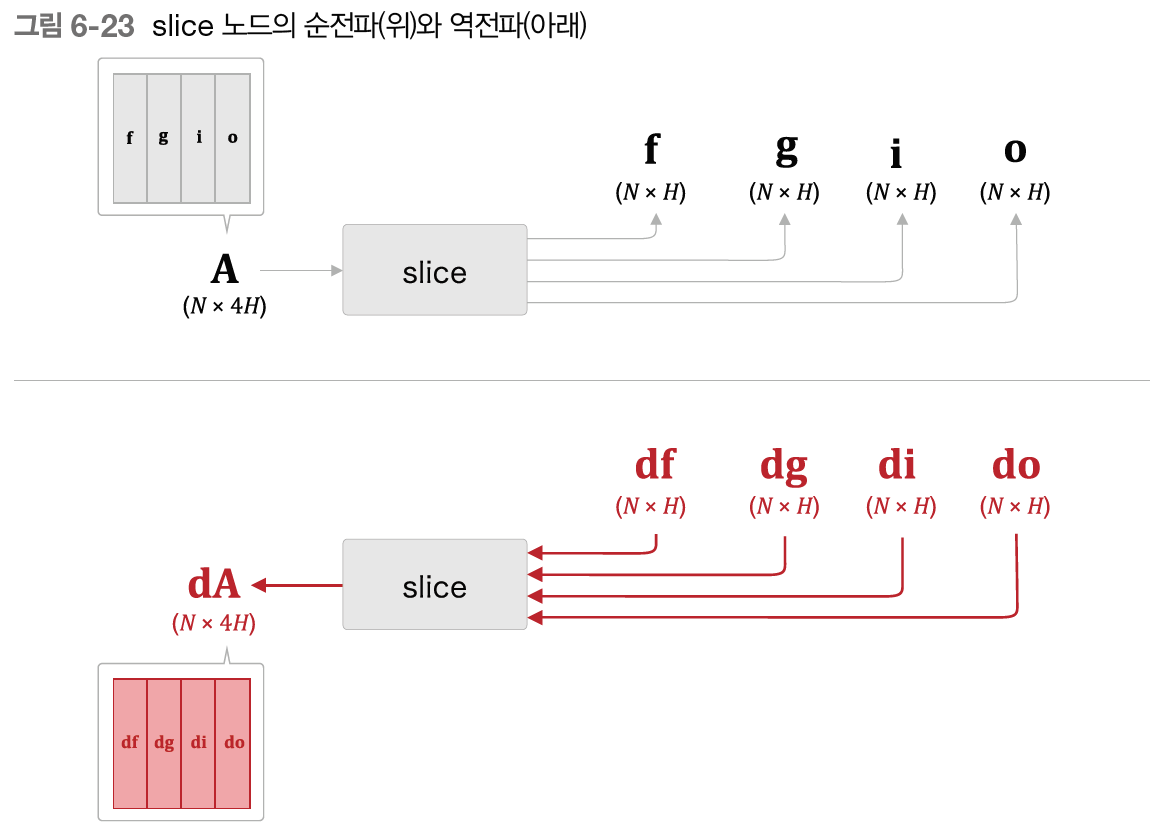
6.3.1 - Time LSTM 구현

Time LSTM은 $T$개분의 시계열 데이터를 한꺼번에 처리하는 계층이다.

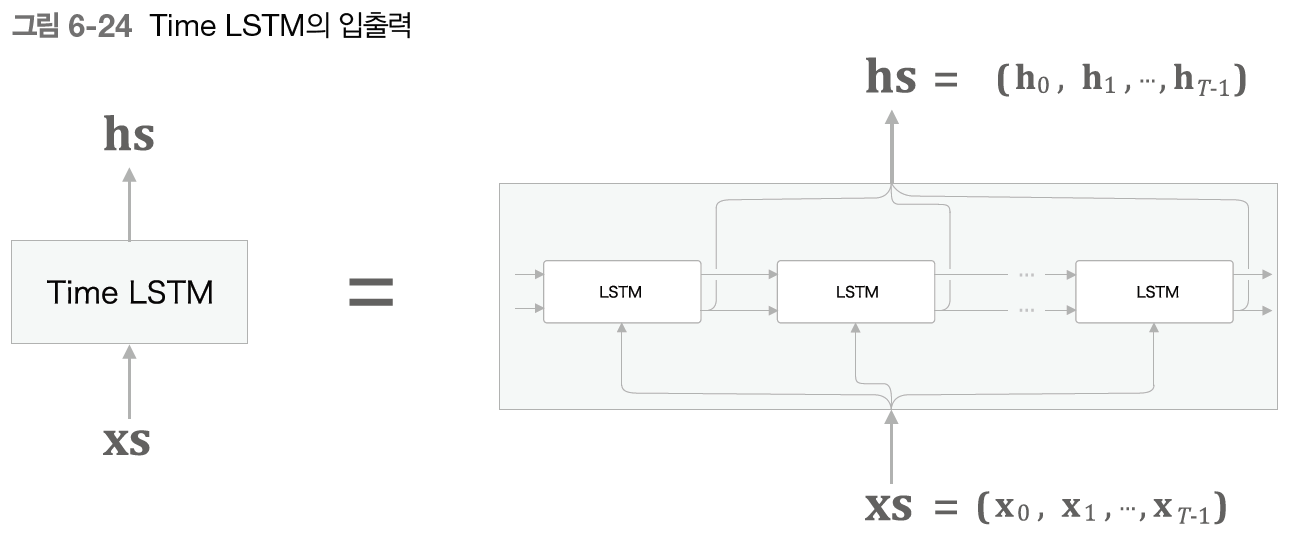
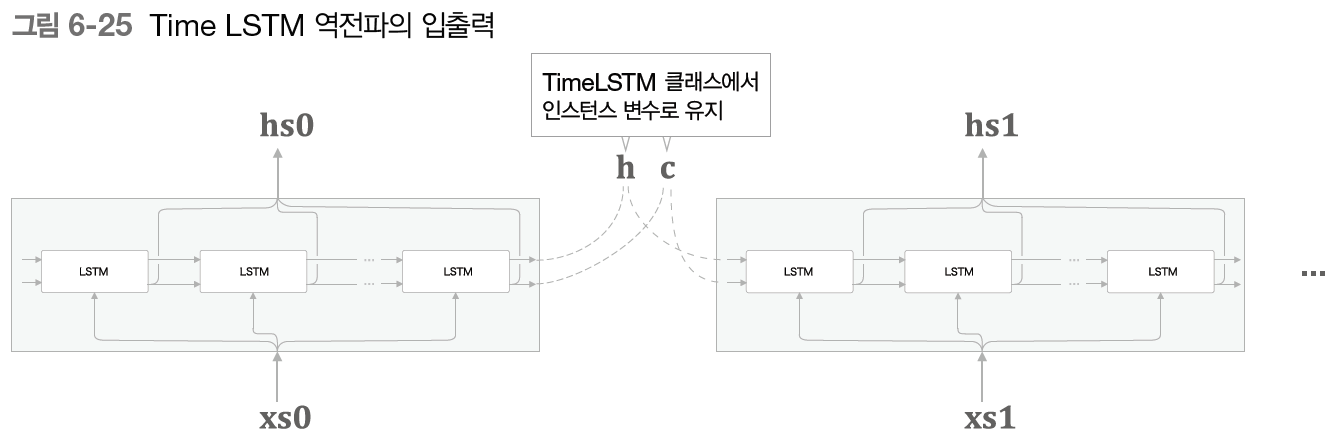
다만 RNN에서 Truncated BPTT를 이용했던 것처럼 여기서도 역전파를 끊고 순전파를 유지한다. 순전파를 유지하기 위해 은닉 상태 벡터와 기억 셀을 유지해 줘야 한다.

6.4 - LSTM을 사용한 언어 모델

원래 언어 모델을 구현하기 위해 RNN 계층을 배웠었다. 그럼 RNN 계층을 개선한 LSTM 계층을 배웠으니 언어 모델도 개선하는 게 좋겠다.

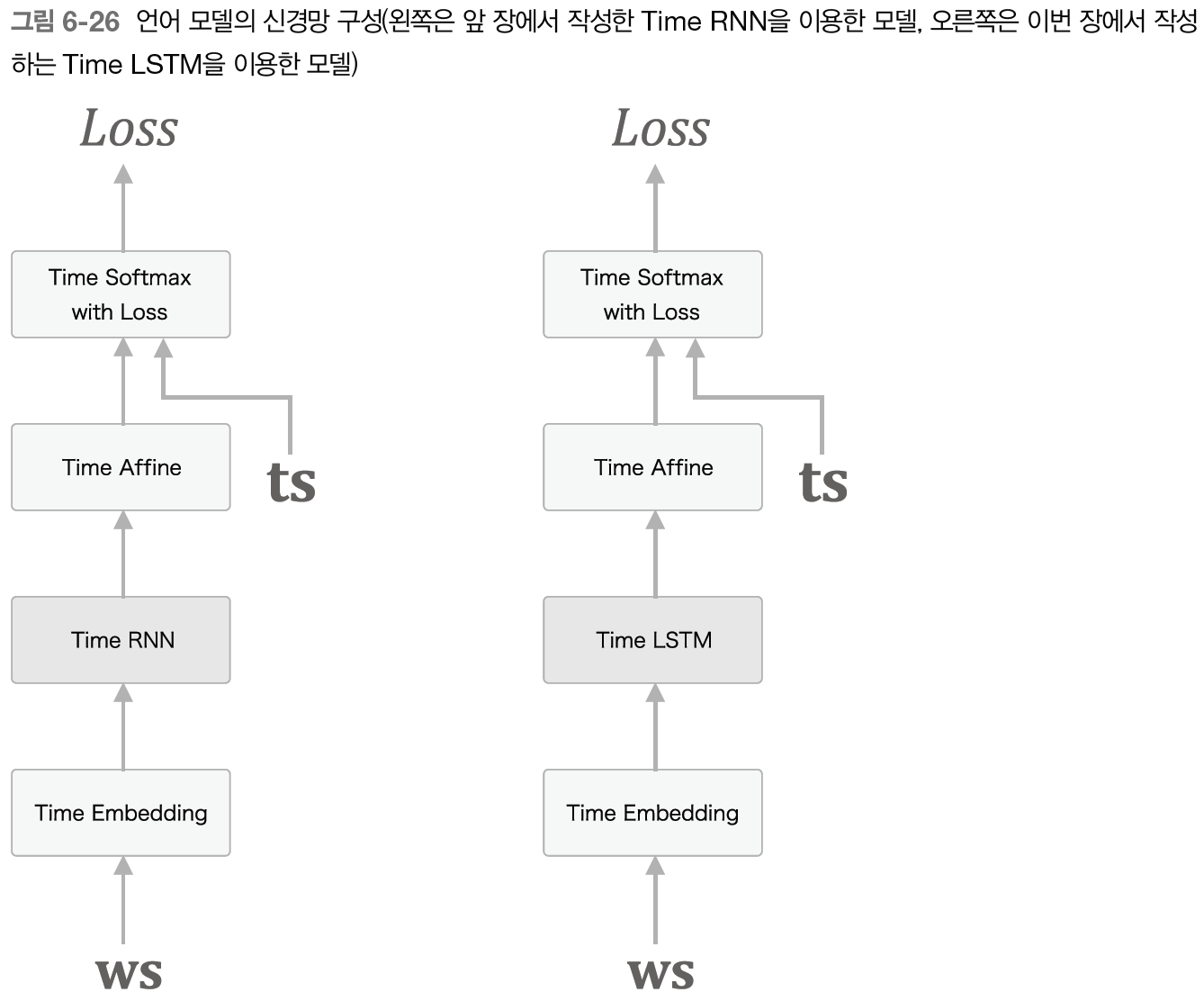
별 차이는 없고 Time RNN 계층이 Time LSTM 계층으로 바뀌었다. 앞 장과의 차이는 LSTM을 사용한다는 점뿐이다.

6.5 - RNNLM 추가 개선

6.5.1 - LSTM 계층 다층화

RNNLM으로 정확한 모델을 만들고자 한다면 많은 경우에 LSTM 계층을 깊게 쌓아 효과를 볼 수 있다.

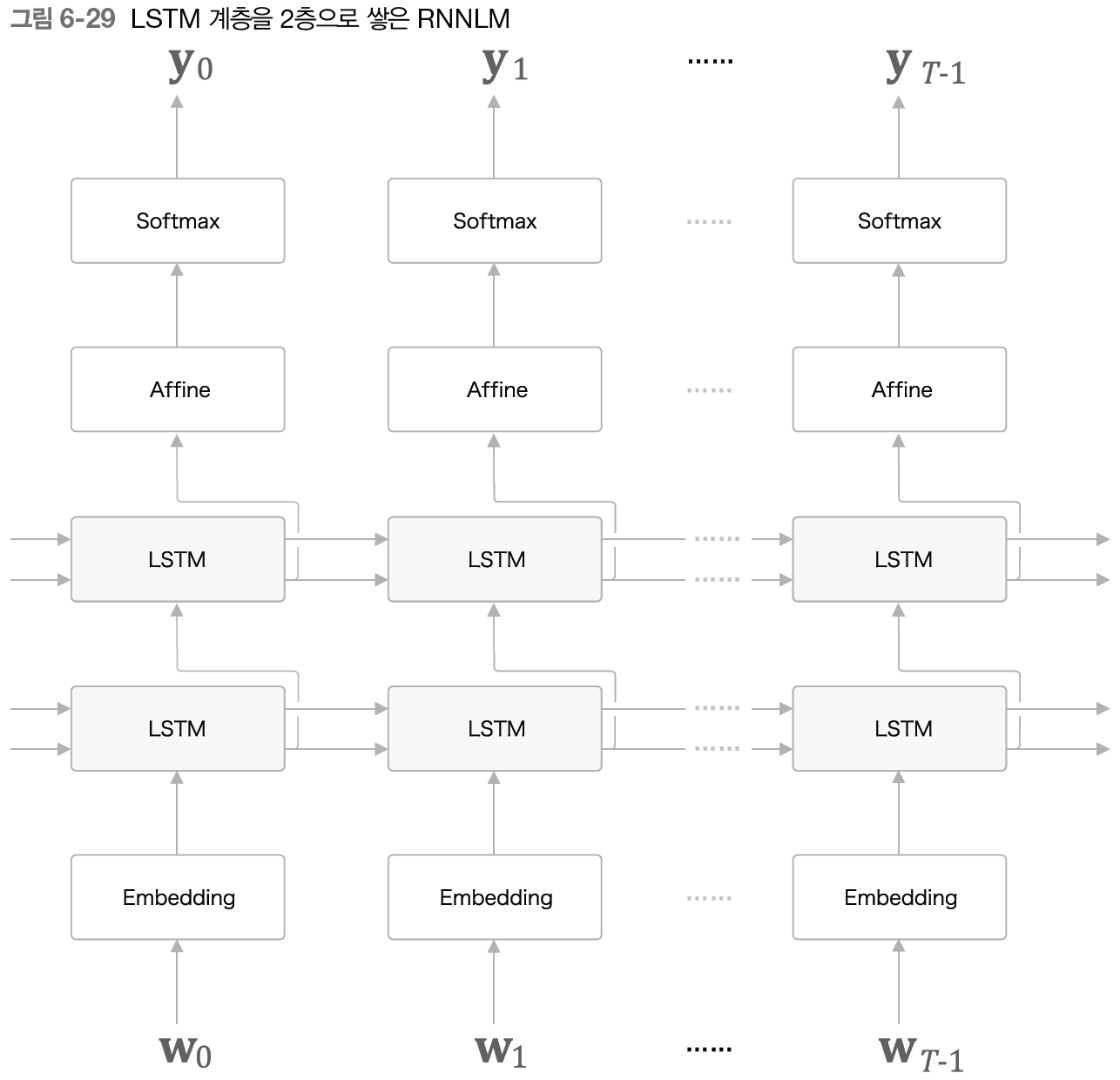
지금까지는 LSTM 계층을 1층만 사용했지만 여러 겹 쌓으면 언어 모델의 정확도가 향상되리라 기대할 수 있다.

위 그림은 2층을 쌓은 경우이다. 첫 번째 LSTM 계층의 은닉 상태 벡터가 두 번째 LSTM 계층에 입력된다. 이런 요령으로 LSTM 계층을 여러 층 쌓을 수 있고, 그 결과 더 복잡한 패턴을 학습할 수 있다. 마치 피드포워드 신경망에서 계층을 쌓는 이야기와 같다.

그렇다면 몇 층을 쌓는 게 좋을까? 쌓는 층 수는 하이퍼파라미터이기 때문에 처리할 문제의 복잡도나 준비된 학습 데이터의 양에 따라 적절하게 결정하는 게 좋다.

6.5.2 - 드롭아웃에 의한 과적합 억제

LSTM 계층을 다층화하면 표현력이 풍부한 모델을 만들 수 있다. 그러나, 이런 모델은 종종 과적합을 일으킨다. 게다가 RNN은 일반적인 피드포워드 신경망보다 쉽게 과적합을 일으킨다.

과적합을 억제하는 방법 중 드롭아웃이 있다. 훈련 시 계층 내의 뉴런 몇 개(예를 들면 50%)를 무작위로 무시하고 학습하는 방법이다. 이거솓 일종의 정규화라고 할 수 있다.

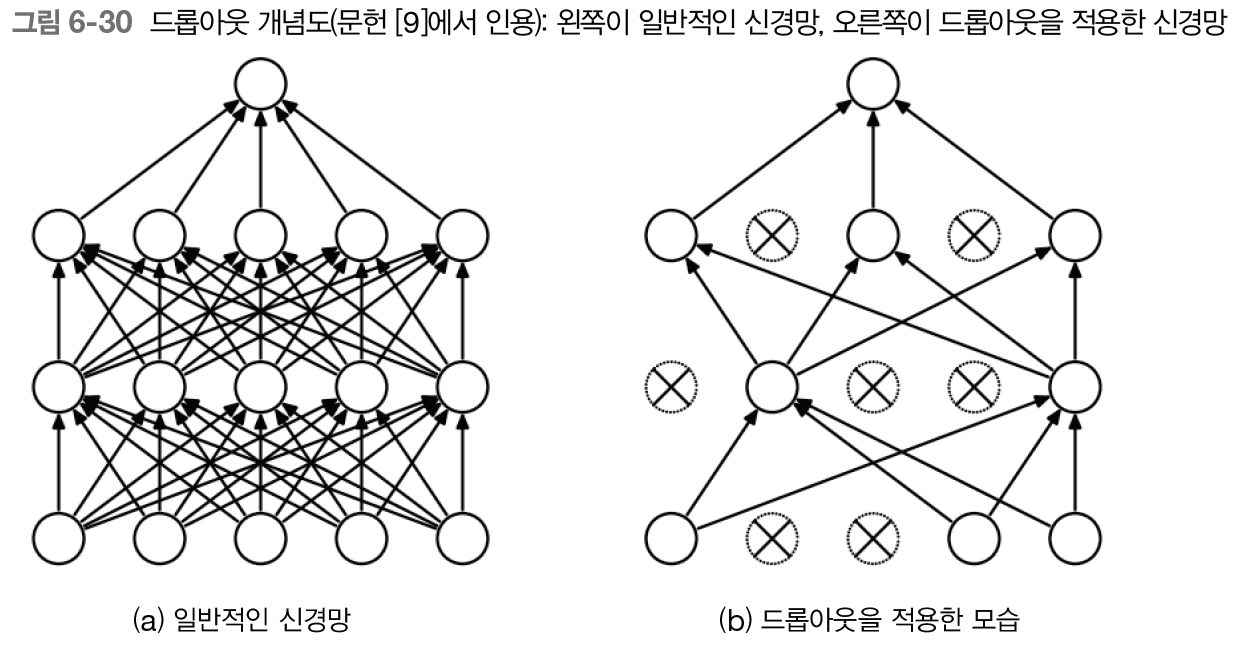
드롭아웃은 무작위로 뉴런을 선택하여 선택한 뉴런을 무시한다. 즉, 앞 계층으로부터의 신호 전달을 막는다. 이 '무작위한 무시'가 제약이 되어 신경망의 일반화 성능을 개선할 수 있다.

그렇다면 RNN을 사용한 모델에서는 드롭아웃 계층을 어디에 삽입해야 할까? 첫 번째 후보는 LSTM 계층의 시계열 방향으로 삽입하는 것이다.

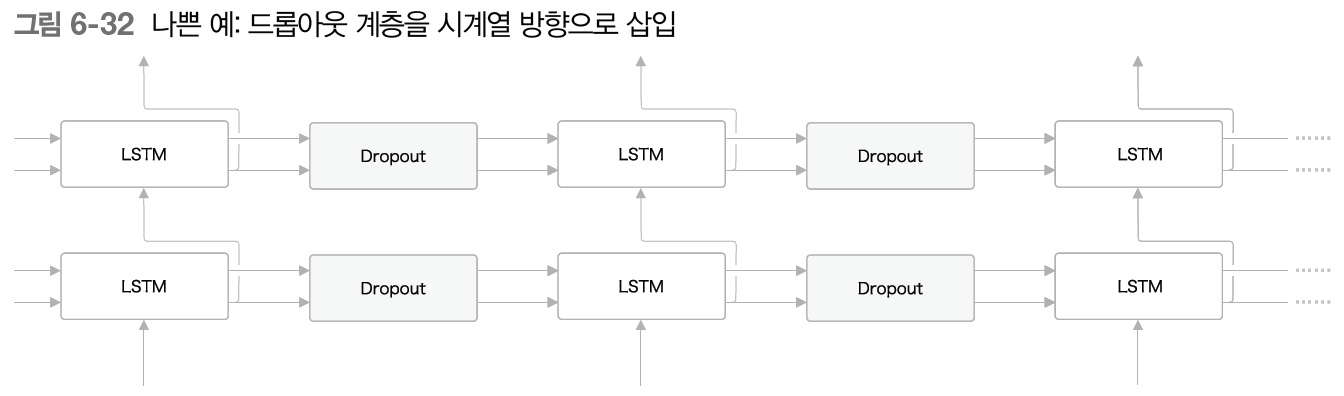
다만 이건 좋은 방법이 아니다. 학습 시에 시간이 흐름에 따라 정보가 사라질 수 있기 때문이다. 즉, 흐르는 시간에 비례해 노이즈가 축적된다. 그렇다면 드롭아웃 계층을 상하 방향으로 삽입하는 방안을 생각해 보자.

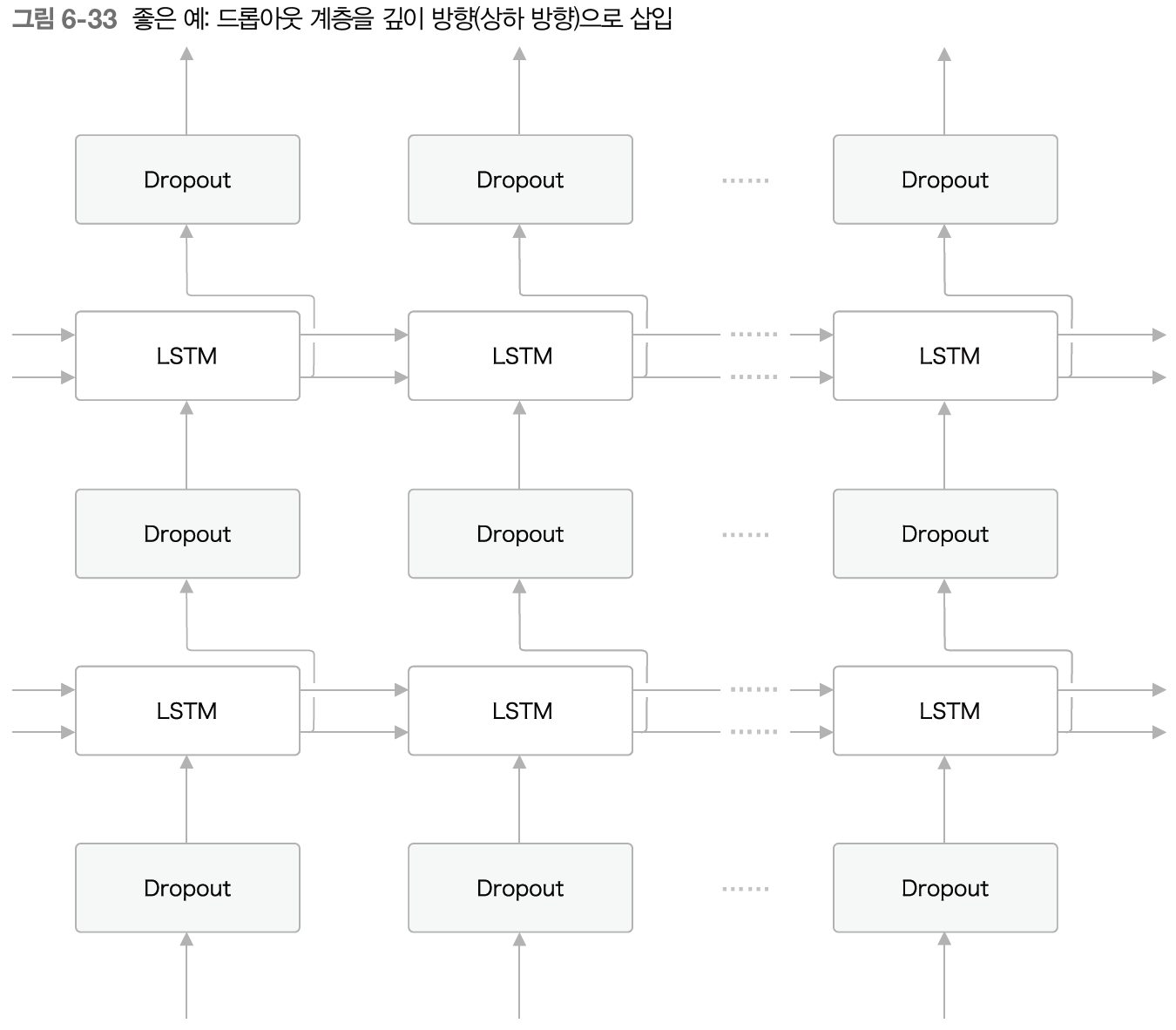
이렇게 구성하면 시간 방향으로 아무리 진행해도 정보를 잃지 않는다. 드롭아웃이 시간축과는 독립적으로 깊이 방향(상하 방향)에만 영향을 주게 되는 것이다.

이렇듯 '일반적인 드롭아웃'은 시간 방향에는 적합하지 않다. 그러나 최근 연구에서는 시간 방향 정규화를 목표로 변형 드롭아웃$^{Variational \space Dropout}$을 제안했고, 시간 방향으로 적용하는 데 성공했다.

변형 드롭아웃은 깊이 방향은 물론 시간 방향에도 이용할 수 있다. 그 구조는 다음과 같다.

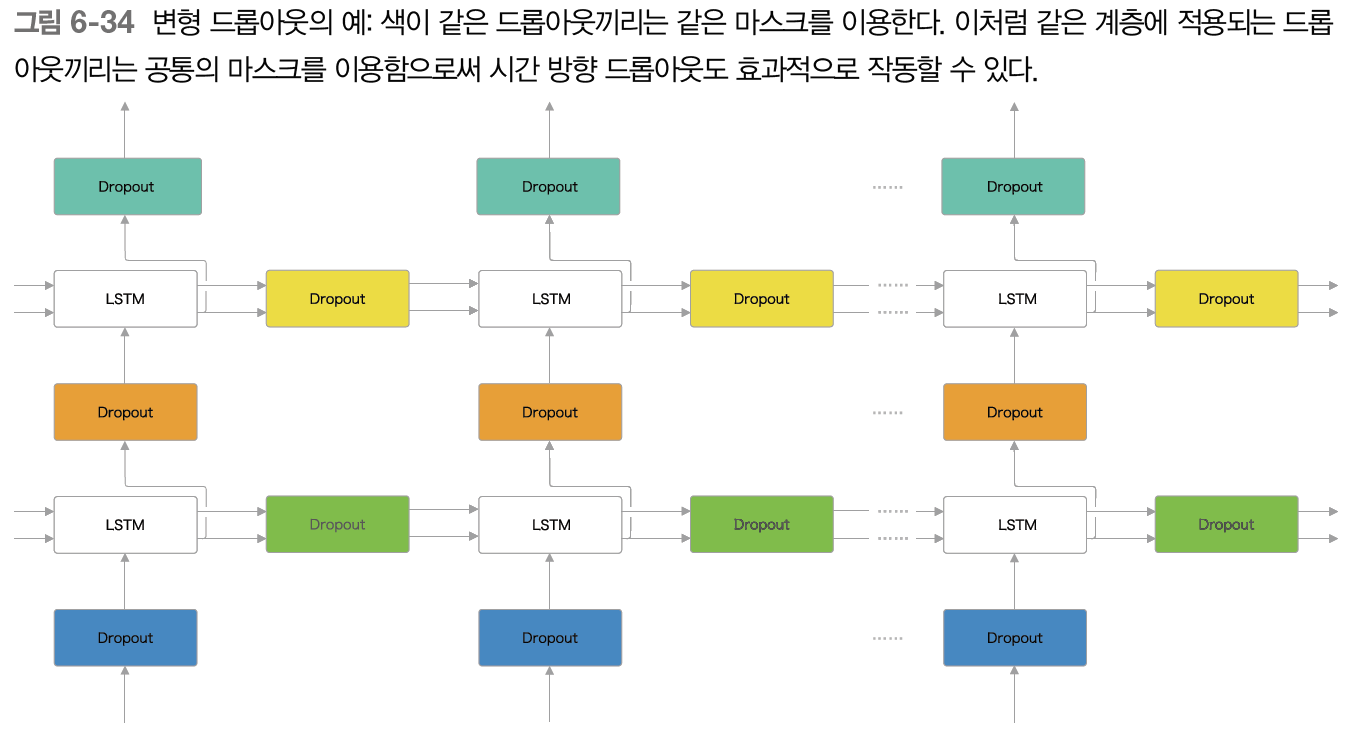
같은 계층에 속한 드롭아웃들은 같은 마스크$^{mask}$를 공유한다. 여기서 '마스크'란 어떤 뉴런을 무시할지에 대한 정보(이진 형태의 패턴)를 말한다. 즉 같은 계층의 드롭아웃들은 같은 방식으로 뉴런을 무시하게 된다.

같은 방식으로 뉴런을 무시하면 정보를 잃게 되는 방법도 '고정'되기 때문에 일반적인 드롭아웃 때와 달리 정보가 지수적으로 손실되는 사태를 피할 수 있다.

6.5.3 - 가중치 공유

언어 모델을 개선하는 아주 간단한 트릭 중 가중치 공유$^{weight \space tying}$가 있다.

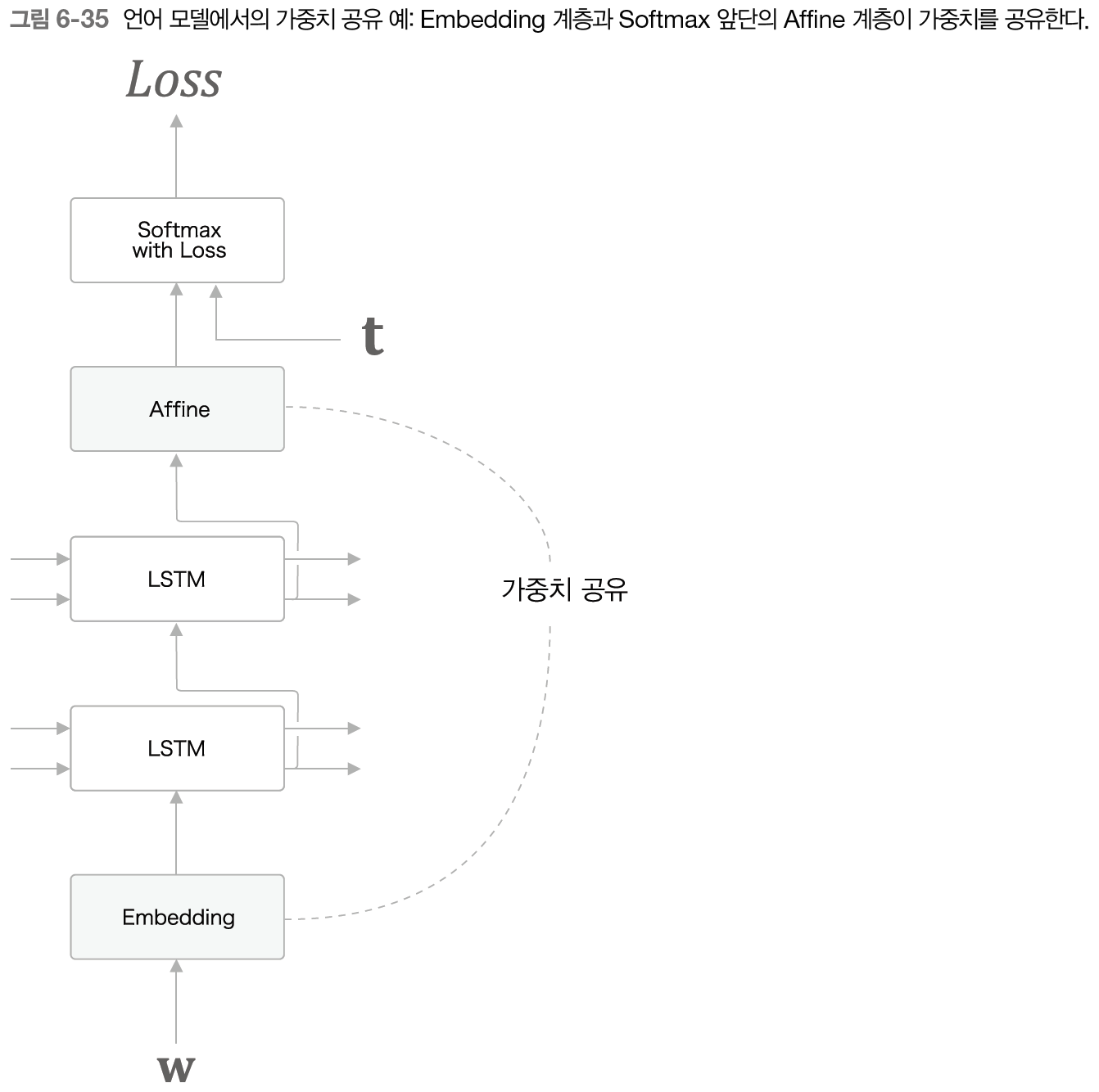
Embedding 계층의 가중치와 Affine 계층의 가중치를 연결(공유)하는 기법이 가중치 공유이다. 두 계층이 가중치를 공유함으로써 학습하는 매개변수 수가 크게 줄어드는 동시에 정확도도 향상된다.

그럼, 가중치 공유를 구현 관점에서 생각해 보자. 어휘 수가 $V$, 단어 벡터의 차원 수를 $D$, LSTM의 은닉 상태 벡터의 차원 수를 $H$라 하겠다.

그러면 Embedding 계층의 가중치는 형상이 $V \times D$이고, Affine 계층의 가중치 형상은 $H \times V$가 된다.

• 이 책에서는 $D$와 $H$가 일치해서 작동하는데, 실제로도 이렇게 구현하는지는 잘 모르겠다.

이때 가중치 공유를 적용하려면 Embedding 계층의 가중치를 전치하여 Affine 계층의 가중치로 설정하기만 하면 된다.