이번 장의 공부 배경

• CH2와 연결됩니다. System and Matrix 참조

Agenda

Elementary Transformations을 조합하여 (Gaussian Elimination을 활용하여) Reduced Row-Echlen form을 만들어서, 간단하게 Inverse Matrix를 얻거나 시스템의 Solution을 구할 수 있다.

하지만, 이 방법론을 적용하다보면 한 가지 문제가 발생할 수도 있다.

• i.e.

$A=\begin{bmatrix} 1 & 1 & -1 \\ 3 & 1 &2 \\3 & 3& -3\end{bmatrix}, \ B=\begin{bmatrix} 2 \\ 5 \\ 6 \end{bmatrix}$
$\rightarrow Equation \ 3개, Unknown \ 3개$

Elementary Transforamtion 적용하면 아래와 같이 표현될 수 있다.

$A^{'}=\begin{bmatrix} 3 & 3 & -3 \\ 3 & 1 &2 \\3 & 3& -3\end{bmatrix}, \ B=\begin{bmatrix} 6 \\ 5 \\ 6 \end{bmatrix}$
$\rightarrow Equation \ 2개, Unknown \ 3개$
$\therefore$ Particular가 아닌, General solution이 발생하게 된다.

그렇다면, 이러한 특이한 케이스는 어떻게 설명해야할까?

Linear Independence로 설명할 수 있다.

자세한 설명에 앞서 반드시 짚고 넘어가야하는 배경 지식을 먼저 학습해본다.

• Groups
• Vector Space
• Vector Subspace

Groups

Definition

set과 operation이 하나의 묶으로 구성되어 있고, 4가지 조건을 만족해야 한다.

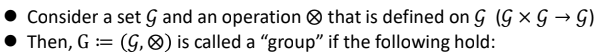
조건 1. Closure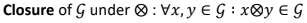
폐쇄적이다 : Set에서 두개의 element를 sampling해서 거기에 operation을 적용하면, Set 내에 있는 element가 된다.

조건 2. Associativity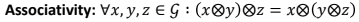
Set 내에서 임의의 고른 임의의 element의 operation을 할 때, 연산의 선후가 바뀌어도 결과 같아야 한다. 단, 연산 순서가 뒤집어지는 것을 의미하는 것은 아니다.
$i.e.) \ a*b*c \neq c*b*a$

조건 3. Neutral element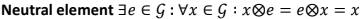

Neutral element 또한, set 안에 있어야 한다.
Set 안의 모든 element 'x'와 operation을 했을 때, operatin과 상관 없이 'x'가 그대로 나오게 해야한다.
$i.e) \ if \otimes = '+'\ \ then, \ e =0 \\\ \ if \otimes = '*'\ \ then, \ e =1$

조건 4. Inverse element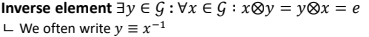

Inverse element역시 set 안에 있어야 한다. 모든 샘플 x에 대해서 y 와 operation 했을 때, neutral element가 나온다면 이 y를 inverse element라고 한다.

Abelian Group

Definition

Group의 subset이다. 즉, group의 4조건을 모두 충족하고 추가로 하나의 조건을 더 만족해야 한다.

조건 5. Commutativity

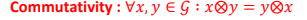
Example

- ($\mathbb{Z}, +)$

Z = 허수 ($a+bi$형태)

1) Closure
$a+bi$와 $c-di$를 '$+$'하면 여전히
$x+yi$형태를 유지한다.

2) Associativity
연산 대상들의 연산 순서를 바꿔도 여전하다

3) Neutral Element
$+$ operation인바, 0이 존재하며
0은 Z허수에 포함된다.

4) Inverse element
$a+bi$의 inverse는 $-a-bi$이며, 역시 허수 안에서 $x+yi$형태 유지한다.

$\therefore (\mathbb{Z}, +) 는 \ Group이다.$

- ($\mathbb{Z}, \times)$

위와 같은 순서로 진행해보면 된다. 다만,

4) Inverse element
$a+bi$의 inverse는 $\frac{1}{a+bi}$이며, $a+bi$가 0이 될 수 있다. $\frac{1}{0}$은 허수에 포함이 안된다.

$\therefore (\mathbb{Z}, \times)는 \ Group이 \ 아니다.$

- ($\mathbb{R^{m \times n}}, +)$

위와 같은 순서로 진행해보면 된다.

$\therefore (\mathbb{R^{m \times n}}, +) 는 \ Group이다.$

Vector Spaces

Definition

Vector Space란, 어떤 벡터를 샘플링해서 더하거나 어떤 스칼라를 곱해도 여전히 가지고 있는 벡터로 표현 할 수 있다는 의미이다.

Inner operation은 set 안에서 두개의 샘플을 뽑았을 때, 여전히 Closure한지를 판단.
Outer operation은 set 안의 하나의 샘플과 임의의 스칼라를 operation했을 때, 여전히 set안에 들어 있는지를 보는 것.

정의상, Inner의 경우 + Outer의 경우 곱하기로 operation이 정해져 있다.

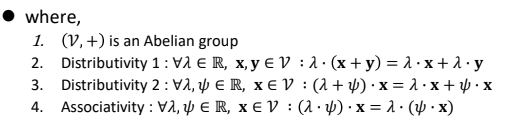
Row and Column Vectors

가장 기본적인 형태의 vector는 column vector를 지칭한다.

Vector Subspace

U는 $\varnothing$이면 안된다.
0의 값을 가질 수 없기 때문이다.

• $(U, +, \cdot )$이 V의 Vector Subspace라는 것을 결정하기 위해서는 아래의 입증이 필요하다.
• $U \neq \varnothing, 0 \in U$ (즉, U는 공집합이면 안되고 원점을 포함하고 있어야 한다.)
• Check the closure of U
  $1. \ \ \ +:U \times U \rightarrow \ U (Inner \ operation) \\ 2. \ \ \ \cdot:\mathbb{R} \times U \rightarrow \ U(Outer \ operation)$

Example - Vector Subspace

if $V \in \mathbb{R}^2$

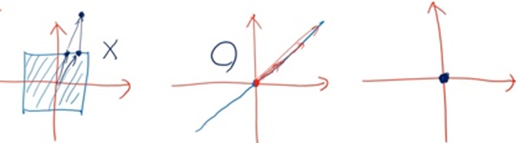
첫 번째 좌표 평면을 보면 해당 set의 샘플을 임의로 추출하여, 더하면 set 범위 바깥의 벡터가 나온다. 그러므로 Vector subspace가 아니다.

두 번째와 세번 째 그림은 Vector subspace이다.