이번 장의 공부 배경

CH3-1과 연결됩니다.

Vector Subspace로 부터 파생되는 Basis의 개념을 간략하게 이해하고, Basis를 얻어서 Linear Combination을 쉽게 구하는 방법을 알아본다.

Vector Space - Closure Property & Basis

Basis란, 벡터의 set인데 그 set내 샘플의 operation으로 Vector Space 상의 모든 벡터를 표현할 수 있는 set. 가령, 대표적인 표준 basis로 $\mathbf{V}\in\mathbb{R^{1 \times 3}}$일 때, {<1,0,0>,<0,1,0>,<0,0,1>} 을 예로 들 수 있다.
이로부터 나올 수 있는 생각이 "벡터 공간의 basis에 있는 벡터의 수를 그 공간의 차원(dimension)이라고"도 할 수 있다.

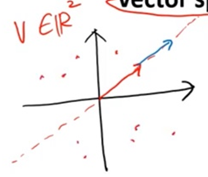
빨간 + 파랑으로 모든 좌표 평면을 나타낼 수 는 없다. 그러므로 이 Set은 Basis가 아니다.

Linear Combination

Definition

Weighted Sum으로 이루어진 벡터(x)들의 합으로 표현 된 form을 의미한다.

Example : 0-vector

k개의 Vector를 linear combination 형태로 표현이 가능하다.

왜냐면 모든 $\lambda$값이 '0'이므로, 이런 식으로 표현할 수 있다. $0=\sum_{i=1}^k0x_i$

어떤 Vector Space에서 어떠한 vector를 뽑든, 그것의 linear combination 형태로 표현이 가능하다.

모든 $\lambda$가 0이어서 0-vector를 얻을 수 있는 것을 Trivial linear combination이라고 한다.

반대로, $\lambda \neq0$이 하나라도 있을 경우, Non-trivial linear combination이라고 한다.

이 특징으로 인하여 Linear Independence라는 특성을 설명할 수 있게 된다.

Linear Independence

Definition

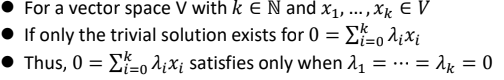
즉, Trivial solution만 있다면, Linear Independence하다.
i.e) $\lambda_1=\cdots=\lambda_k=0$일 경우 Linear Independence하다고 표현한다.

Linear dependence

Non-Trivial solution이 있다면, Linear dependence하다.
i.e)단 하나라도 $\lambda_i\neq0$일 경우 Linear dependence하다고 표현한다.

결국 어떤 A 매트릭스를 계산하는데, 여기서 linear equation을 푸는 것이 목표인데,

어떤 관계성을 가지는 equation들이 여러개 존재하는 상황을 알아보자. 어떻게 찾아내고 어떻게 표현할지를 위하여 배우는 것이다.

Linear Independence - Properties

• k vectors는 Linearly Independent하거나 dependent할 뿐 다른 형태의 특성이 있지 않다.
• k개 vector에 하나라도 0벡터가 있다면, Non-Trivial solution이 존재한다는 의미이며, 이는 곧 linearly dependent하다.

$\\$

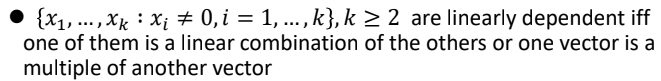
$\mathbf{A}=\begin{bmatrix}식a\\식b\\식c\end{bmatrix}$일때,

$c=a+b$ 처럼 다른 linear equation의 combination으로 다른 equation을 나타낼 수 있거나,

$c=\lambda a$ 처럼 표현될 때 linearly dependent하다고 표현한다.

정리:
$0=\sum_{i=1}^k\lambda_ix_i 가 only\ trivial일 때, linearly independent하다는 표현을 위와같이 풀어 쓸 수도 있는 것이다.$

• k개 벡터$(x_1,\cdots,x_k)$에다가 m개의 linear combination을 할 때,
  $m>k$인 경우, linearly dependent하다.

i.e) 2차원 평면에서 하나의 벡터는 두개 벡터의 조합으로 충분히 얻을 수 있다. 만약 여기서 3개의 linear가 있는 경우(3개의 벡터), linearly dependent하다고 표현한다.(=뽑을 수 있는 벡터의 차원수보다 많은 수의 벡터가 추출되는 경우)

Gaussian Elimination

Gaussian Elimination을 이용하여 Linearly Independence를 체크할 수 있다.

• 샘플링한 k개의 벡터를 각각의 Column으로 해서 매트릭스 A를 빌드한다.
• Gaussian elimination을 반복하여 Row-Echelon form을 구한다.(여기서는 Reduced 버전을 구할 필요도 없다. Pivot/Non-Pivot column의 존재만 확인하면 되기 때문이다.)

Example

$A\in\mathbb{Q^{2\times3}}\rightarrow\ Row-Echelon\ Form\rightarrow \begin{bmatrix}2 & 1 &4 \\ 0 & 0 & 3\end{bmatrix}$

• 이 경우 Pivot column은 첫번째, 세번째이다.
  Non pivot column은 두번째이다.

• Pivot column 끼리는 각각 변형하여 다른 pivot column을 나타낼 수없다. = 서로 다른 column끼리 독립성이 있다. = 영향을 끼칠 수 없다.

• 반대로, Non pivot column은 다른 column(ex. pivot column)을 변형하여 나타낼 수 있게 된다.

• 이를 통해 알 수 있는 것은 만약 모든 column이 pivot column이라면, 모든 column은 linearly independent하다. 반대로, non-pivot column이 단 하나라도 있다면, column들은 linearly dependent하다고 표현이 된다.

Linear Combination - Compact Form

$\mathbf{V} :$ Vector space
$\mathbf{k} :$ Linearly independent vector의 개수(k개, $\mathbf{b_1},...,\mathbf{b_k}$)

$\mathbf{b}$ : basis를 의미한다.(linearly independent하면 basis가 포함되어 있으므로 종종 이렇게 표시한다)

m linear combination :

• $\mathbf{x_1} =\sum_{i=1}^k\lambda_{i1}\mathbf{b_i},\cdots,\mathbf{x_m} =\sum_{i=1}^k\lambda_{im}\mathbf{b_i}$

여러개의 linear equation의 combination을 간단하게 matrix * vector 형태로 나타낼 수 있다. $\rightarrow$ Compact form

$\mathbf{B}=\begin{bmatrix}\mathbf{b_1},\cdots,\mathbf{b_k}\end{bmatrix}$

$\mathbf{\lambda_j}=\begin{bmatrix}\lambda_{1j} \\ \cdots \\ \lambda_{kj}\end{bmatrix}$($j = 1,\cdots,m$)

$\therefore$ $\mathbf{x_j}= \mathbf{B\lambda_j}$

여기서 한가지 의문이 들 수 있다.
$\mathbf{B}$는 linearly independent한 벡터들의 집합이다. 그렇다면 위의 compact form으로 구해진 $\mathbf{x}$(m개의 x벡터) 역시 linearly independent할까?

결론적으로는 $\mathbf{\lambda}$가 linearly independent하다면 그러하다. 다시 Linear Independence의 정의를 이용하여 보자.

즉, Trivial solution만 있다면, Linear Independence하다.
i.e) $\lambda_1=\cdots=\lambda_k=0$일 경우 $\mathbf{x}$는 Linear Independence하다고 표현한다.

우리는 $\mathbf{x}$가 Linearly Independent하다고 증명하기 위하여 다시 $0=\sum\lambda\mathbf{x}$에서 $\lambda$가 모두 0만 존재하므로 trivial 솔루션이 있고 그래서 $\mathbf{x}$가 Linearly Independent하다는 것을 유도할 것이다.

그러므로 새로운 스칼라 값인 $\psi$를 사용하여 식을 전개해본다.

$0=\sum_{j=1}^m\psi_j\mathbf{x}_j=\sum_{j=1}^m\psi_j\mathbf{B\lambda}_j=\mathbf{B}\sum_{j=1}^m\psi_j\mathbf{\lambda}_j$

애초에 $\mathbf{B}$는 Basis로서, Linearly independence를 전제하였기 때문에 0이 될 수 없다. 또한, 모든 sum에 대해 적용되기 때문에 상수처럼 여겨서 맨 앞으로 빼내어 수식을 정리할 수 있다.

결국, $\mathbf{x}$가 linearly Independent한가에 대한 질문이 $\mathbf{\lambda}$가 linearly Independent한가에 대한 질문으로 바뀌게 된다.

이 내용은 나중에 Dual이라는 문제와 엮여서 x의 linear Independence를 구하기 어려울 때, $\lambda$로 대체하여 구한다.

Example

$b_1,b_2,b_3,b_4\in \mathbb{R}^4$이다. b는 basis로서 linearly independent하다. 이 때, x는 Linearly Independent한가?

$x_1 = b_1 -2b_2+b_3-b_4\\ x_2 = -4b_1 -2b_2+ \ \ 4b_4\\ x_3 = 2b_1 +3b_2-b_3-3b_4\\ x_4 = 17b_1 -10b_2+11b_3+b_4$

Sol)

matrix form으로 변형한다.
$\mathbf{x}=\begin{bmatrix}1 & -4 & 2 & 17\\ -2 & -2 & 3 & 10\\ 1 & 0 &-1 &11\\ -1 & 4 & -3 & 1\end{bmatrix}\begin{bmatrix}b_1\\b_2\\b_3\\b_4\end{bmatrix}$

Gaussian elmination을 이용하여 Row-Echlen Form으로 변형해준다.

$\mathbf{A}=\begin{bmatrix}1 & -4 & 2 & 17\\ -2 & -2 & 3 & 10\\ 1 & 0 &-1 &11\\ -1 & 4 & -3 & 1\end{bmatrix}$$\rightarrow$$\begin{bmatrix}1 & -4 & 2 & 17\\ 0 & -10 & 7 & 24\\ 0 & 4 & -3 & -6\\ 0 & 0 & -1 & 18\end{bmatrix}$

$\rightarrow$

$\begin{bmatrix}1 & -4 & 2 & 17\\ 0 & 4 & -3 & -6\\ 0 & -10 & 7 & 24\\ 0 & 0 & -1 & 18\end{bmatrix}$$\rightarrow$$\begin{bmatrix}1 & 0 & -1 & 11\\ 0 & 4 & -3 & -6\\ 0 & 0 & -1/2 & 15\\ 0 & 0 & -1 & 18\end{bmatrix}$

$\rightarrow$

$\begin{bmatrix}1 & 0 & 0 & -7\\ 0 & 1 & 0 & -15\\ 0 & 0 & 1 & -18\\ 0 & 0 & 0 & 0\end{bmatrix}$

Column 1, 2, 3은 Pivot column이지만
Column 4는 Non Pivot 이다. 그러므로 Linearly Dependent하다.