Vector & Matrix
Vector
Definition
Elements of R (tuples of n real numbers)
스칼라 값(a)들의 묶음
Notation
a≡a=⎣⎢⎢⎢⎢⎢⎡a1a2⋯an−1an⎦⎥⎥⎥⎥⎥⎤∈Rn
표현 : lowercase letter(소문자) + bold
n : element의 개수
Operations with Vector
덧셈
Scalar 값을 모든 element에 곱한다 (λ∈R)
λa=λ⎣⎢⎢⎢⎢⎢⎡a1a2⋯anan⎦⎥⎥⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎢⎡λa1λa2⋯λan−1λan⎦⎥⎥⎥⎥⎥⎤∈Rn
기존의 입력된 벡터의 사이즈가 그대로 유지 된다.
Matrix
Definition
Elements of Rm×n (tuples of n real numbers with 2 dimensions)
Notation
A=⎣⎢⎢⎢⎡a11a21⋯am1a12a22⋯am2⋯⋯⋯⋯⋯⋯⋯⋯a1na2n⋯ann⎦⎥⎥⎥⎤∈Rm×n
표현 : Uppercase letter(대문자) + bold
해석 : a12 -> (1,2)
Operations with Matrix
- Matrix Addition
덧셈
- Matrix Multiplication
Multiply and sum for every row and column
A∈Rn×h,B∈Rh×m
AB=C∈Rn×m
AB=BA
Identity Matrix
Definition
In Rn×n, containing 1 on the diagonal and others are all '0'
Diagonal : aij=1, (only i=j)
Properties
ImA=AIn=A (Im=m×m 행렬)
Solving linear equations by using vector & matirx
Systems of Linear Equations
- a11x1+⋯+a1nxn=b1
- ⋯
- am1x1+⋯+amnxn=bm
x : unknown, a : user parameter, : result
해석 : 사용자가 a를 바꿔가며 b라는 결과가 나올 때 x는 미지수임.
Linear Equations to Vectors
⎣⎢⎡a11⋯am1⎦⎥⎤x1+⎣⎢⎡a12⋯am2⎦⎥⎤x2+⋯+⎣⎢⎡a1n⋯amn⎦⎥⎤xn=⎣⎢⎡b1⋯bm⎦⎥⎤∈Rn
Linear Equations to Vector & Matrix
의의 : 복잡한 Linear equation을 단 3개의 variable로 표현할 수 있게 된다.
Operations for Matrix - Inverse
Square matrix에 대해,
A가 B의 Inverse matrix라고 한다면
AB=In=BA
Notation A−1=B
- iff Inverse matrix가 있다면, Regular / Invertible / Nonsingular하다고 표현.
- 역행렬의 간단한 표현식은 구글에서 찾아 볼 것.
Operations for Matrix - Transpose
A∈Rm×n 에 대하여, B∈Rn×m이라면 B를 A의 Transpose라고 한다.
Notation : B=AT
이 때 bij=aji 이다.
i.e.)
A=⎣⎢⎡a11a21a31a12a22a32⎦⎥⎤∈R3×2
AT=B=[a11a12a21a22a31a32]∈R2×3
Operations for Matrix - Properties
AA−1=I=A−1A
(AB)−1=B−1A−1
(A+B)−1=A−1+B−1
(AT)T=A
(A+B)T=AT+BT
(AB)T=BTAT
Operations for Matrix - Symmetric Matrix
- A=AT 라면, A는 Symmetric하다
- Transpose 하면 사이즈가 바뀔 수 있기 때문에 위의 조건이 나온 것
- 그 결과 오직 square matrix만 symmetric할 수 있다.
- symmetric matrices의 합은 여전히 symmetric하다. [(A+B)T=AT+BT]
Solving Linear Equations
- Particular Solution
해 (특정한 값)
i.e)
if Ax = b,
[100182−412]⎣⎢⎢⎢⎡x1x2x3x4⎦⎥⎥⎥⎤=[428]
∴x=⎣⎢⎢⎢⎡42800⎦⎥⎥⎥⎤▶ParticularSolution
- General Solution
시스템을 성립시키는 모든 해를 수식의 형태로 표시한 것.
#unknowns > #equations
x=⎣⎢⎢⎢⎡42800⎦⎥⎥⎥⎤+λ1⎣⎢⎢⎢⎡82−10⎦⎥⎥⎥⎤+λ2⎣⎢⎢⎢⎡−4120−1⎦⎥⎥⎥⎤(λ1,λ2∈R)
Elementary transforamation of matrix
- 주어진 equation system을 우리가 풀어주기 쉬운 형태로 변형시키는 과정 즉, 간단한 수식으로 변형시켜 주는 것. Ax=b→A′x=b′
- 변형을 해도 해는 동일해야 함. 해가 달라진다면 잘못 계산한 것.
i.e)
1. 두 식의 순서를 바꾼다.(row 변형)
개념
[a11a21a12a22]⇒[a21a11a22a12]
b도 위치 변형시켜줘야 한다.
표현 예시
Ax=b→E1Ax=E1b
E1=⎣⎢⎡100001010⎦⎥⎤
2번째, 3번째의 equation 순서를 뒤집는다.
2. 수식에 스칼라 값을 곱한다.
개념
[λa11a21λa12a22]⇒[λa11a21λa12a22]
b도 λ 곱해줘야 한다.
표현 예시
Ax=b→E2Ax=E2b
Constant를 곱해주는 Equation 순서에 해당되는 곳에만 λ 를 둔다.
E2=⎣⎢⎡λ00010001⎦⎥⎤
3. 두식을 더한다 (row 합성)
개념
두 식을 더하는 것을 매트릭스로 표현한다. E3를 곱해서 전개해보면 알 수 있다.
표현 예시
Ax=b→E3Ax=E3b
E3=[1011]
Definition
- All rows that contain only zeros are at the bottom of the matrix
- We can obtain R-E form by using the elementary transformations
로우 애슐런 폼은 이후 과정에서도 꾸준히 나오는 계산 기법 중 하나이다. "0만 포함하는 row는 매트릭스의 가장 아래에 위치하고 있다"고 표현하는데, 사실 글만으로는 이해가 안 될 수 있다.
정확한 방식인지는 모르겠으나, 이렇게 한 번 이해 해보면 쉬울 것 같다.
⎣⎢⎡100000010120233⎦⎥⎤
Pivot
-
First nonzero number from the left at each row
-
R-E form으로 매트릭스가 변형이 된다면, Row의 element 중에서 가장 먼저 0이 아닌 값이 나오는 경우가 있다. 그 값을 pivot이라고 한다.
-
Basic Variables : R-E form에서 pivot이 존재하는 column에 대응되는(곱해지는) variable(x1,x3,x5)을 의미한다.
-
Freee Variables : 나머지 Varialbes
⎣⎢⎡100000010120233⎦⎥⎤⎣⎢⎢⎢⎢⎢⎡x1x2x3x4x5⎦⎥⎥⎥⎥⎥⎤
Definition
- R-E form을 간소화 시킨 버전이다.
- 모든 pivot은 1로 만들어야 한다.
- pivot은 자기가 포함된 column 내에서 유일한 nonzero값인 형태여야 한다.
⎣⎢⎡100200010340001⎦⎥⎤
Necessity
- Non-Pivot column들을 쉽게 찾을 수 있다.
i.e)
- General Solution을 쉽게 찾을 수 있다.
해당 방법에 대해서는 필요시 찾아보길 바란다.
Gaussian Elimination
Elementary transformation을 반복하여 reduced row-echelon form을 얻는 알고리즘을 의미한다.
Calculation of Inverse Matrix
Gaussian Elimination을 이용하여 Inverse Matrix를 구하는 것이 중요하다.
-
만약 매트릭스에 determinant가 존재한다면, Inverse Matrix도 존재한다.
-
A 매트릭스의 Inverse matrix를 계산하고싶다면, A 매트릭스에 I를 붙여 놓고, Gaussian elimination을 사용하여 A 매트릭스 위치에 자리하는 A매트릭스를 I로 만들어 버린다. 이 경우, 기존 I자리의 I는 A−1로 변형된다.
-
흐름을 표현하자면,
[A∣In]→(Gaussian Elimination적용)→[In∣A−1]
-
표현 예시
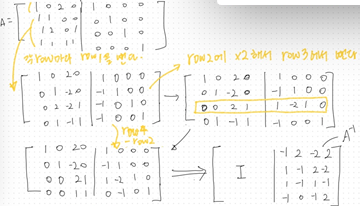
Moore-Penrose Pseudo-Inverse
-
Ax=b,A∈Rm×n
A가 Square matrix가 아닌 경우가 있을 수도 있다. 이 때의 Inver Matrix를 구하는 방법.
-
Ax=b→ATAx=ATb→x=(ATA)−1ATb
Moore-Penrose Pseudo-Inverse
At≡(ATA)−1AT
- (ATA)−1는 square matrix가 된다.
- Moore-Penrose Pseudo-Inverse의 복잡한 형태가 그냥 square를 곱하는 것보다 계산에 더 안정성을 줄 수 있는 경우도 있다고 한다.

