Introduction

What's the data?

"Data is a collection of discrete values that convey information" - Wikipedia

Data Representation

아래는 데이터의 대표 예시인 '표'를 통해 데이터를 이해해보도록 한다.

표(TABLE)

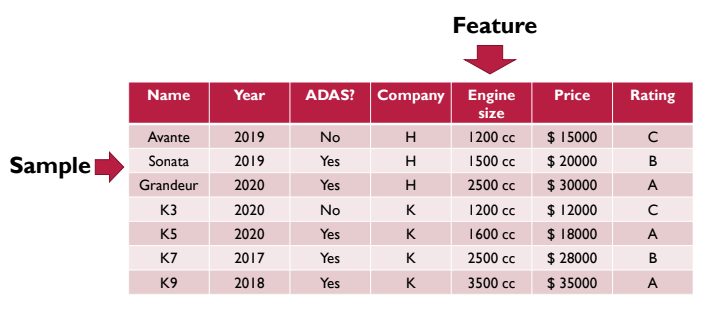
표의 구성성분인 행/열은 각각 아래와 같이 표현할 수 있다.

• Sample : 가로줄 (각 샘플은 여러 Feature가 개 묶여 있는 형상)
• Feature (or Feature Channel) : 세로줄

feature에 들어갈 수 있는 값은 정말 다양하다.
아래의 예시들에서는 이미지, 그래프, 텍스트 등 다양한 샘플 데이터가 표로 구성되고 feature와 같이 표현되는지를 살펴본다.

Feature에 따른 구분

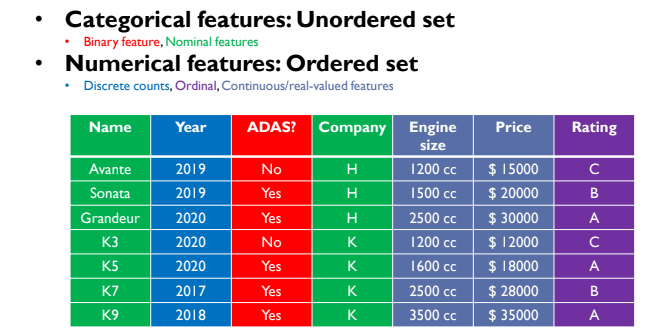
데이터 값에 순서 유/무에 따라 feature를 구분할 수 있다.

Categorical features : Unordered set

• Binary feature(Yes or No) : 소위 기냐 아니냐고 표현할 수 있다. 예시의 표에서는 ADAS 기능의 유무로 표현되고 있다.
• Nominal features(이름) : 이름이 있는 값이다. 무수히 많은 값이 저장될 수 있다.

위 두 feature는 순서를 매길 수 없는, 필요가 없는 데이터이다.

Numerical feature : Ordered set

• Discrete counts : 년/월/일처럼 어느 정도 정해진 숫자만 표현한다.
• Ordinal : 순위라고 이해하면 좋다. 알파벳으로 순서를 매겨놓았다.
• Continous/real-valued features : 가격, 제품 사이즈 등과 같이 어떠한 숫자도 나올 수 있는 데이터 값이다.

Bag of Words

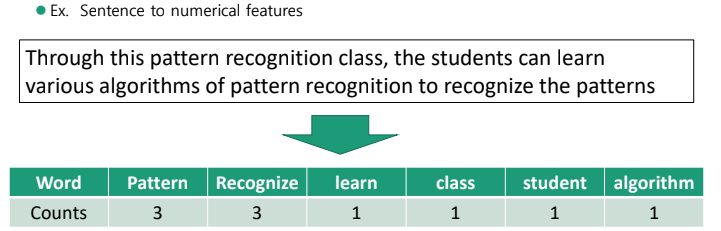
단어들의 순서는 전혀 고려하지 않고, 단어들의 출현 빈도(frequency)에만 집중하는 텍스트 데이터의 수치화 표현 방법이다.
출처 : wikidocs

Image Data & Graph Data

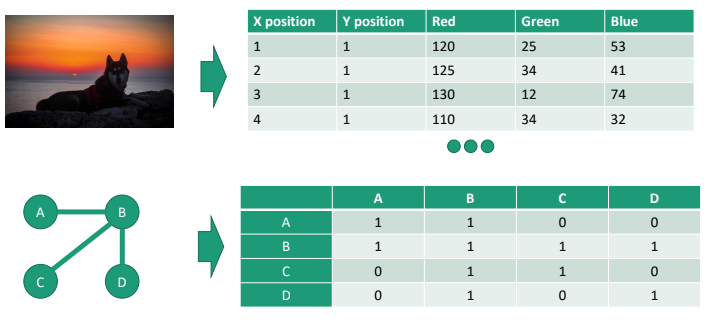
• 이미지 좌표 당 RGB값이 픽셀 개수만큼 존재하는 것을 표현한다. 사람이 보는 이미지를 feature matrix form으로 전환할 수 있다.

• 그래프를 활용하기도 한다. 물체/사람 간의 관계를 표현할 때 사용하는 것. ex) SNS에서 팔로우 / 언팔로우 한 사람끼리 연결/ 미연결을 시키는 것
  그래프를 Adjacency matrix로 표현하여 연결성을 표로 표현한다. (노드 개수만큼 feature 숫자가 표현된다. - AA, BB, CC 자기 자신은 1로 표현한다.)

Feature Aggregation

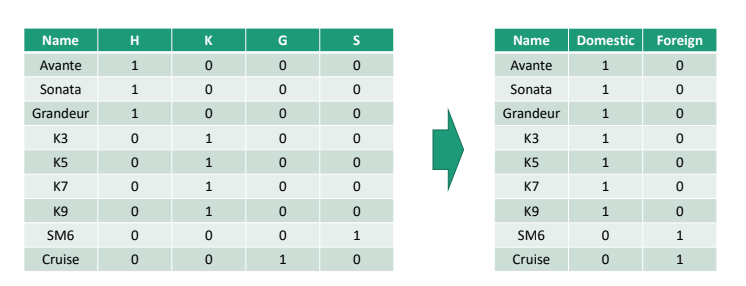
Feature를 줄일 수도 있다. 테이블 내에 불필요한 feature가 존재할 수 있기 때문이다. 가령, 자동차의 국산/외산으로만 구분하고자 할 때, feature를 합치는 것이다. feature의 크기가 계산량이므로 가능하다면 크기는 줄어들수록 좋다.

Feature Selection

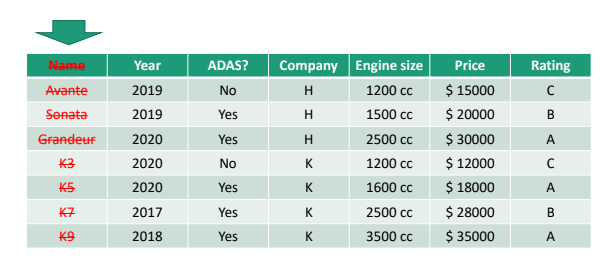
Feature 이름이 필요 없을 때가 있다. 가령, 연초에 진행되는 정기 자동차 점검의 경우 자동차 이름 별로 검사 여부가 결정나지 않는다. 즉, 자동차 이름이 결과에 영향을 주지 않는 값이므로 불필요 feature를 골라낸다.

Feature Categorization

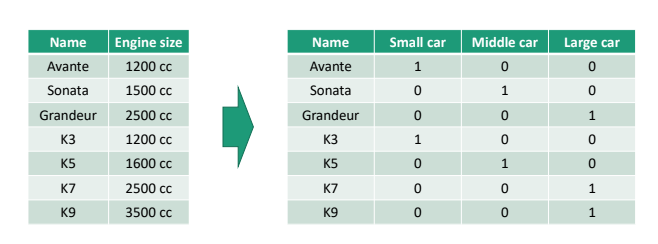
상세한 숫자가 필요 없는 상황이라면, 그 값을 단순하고 다르게 표현하는 것. 가령, 배기량 숫자에 따라 차종을 3가지로 feature를 단순화시킨다. (cf. 선택할 수 있는 숫자의 range를 Variation이라고 표현한다)

Feature Scaling

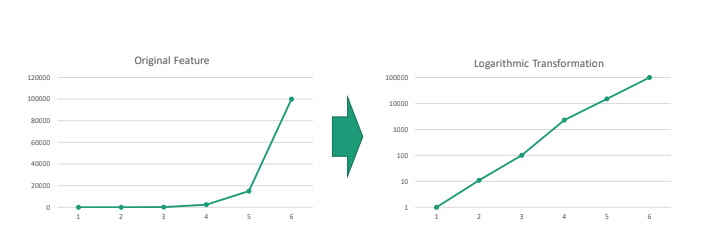
자동차와 비행기는 feature의 데이터 사이즈가 너무 차이가 난다. 그래서 자동차 간 데이터 사이즈 차이가 줄어들어서 feature 기반으로 자동차 간의 등급 구분이 어려워진다.

이 때, feature scaling 방법으로 log를 씌우면 된다. 차이가 적어도 상대적인 차이를 키워서 데이터 간 비교를 용이하게 할 수 있게 한다.

Data - Feature & Label

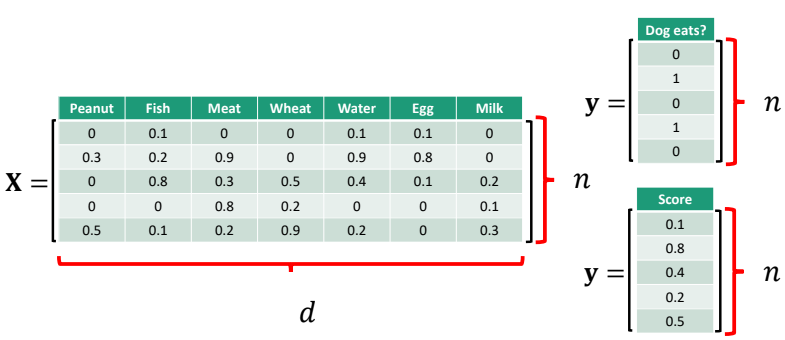
sample : n
feature : d

X = n x d (x : matrix)

matrix 기반으로 주요 성분을 뽑아내거나 머신러닝 모델을 뽑아낼 수 있다. 이것이 머신러닝을 위한 공업수학을 배우는 주목적이다.

Label : 사람의 결정을 표시해 둔 데이터 값이다.
가령, 강아지가 먹을 수 있을지 없을지만 본다면 0 / 1 두 라벨만 존재한다.
혹은 점수를 매긴다면, 라벨은 점수가 될 수 있고 0 ~ 1 사이 모든 숫자가 라벨이 될 수 있다.

cf) 라벨은 y로 사용한다.
대게 Matrix는 대문자(Capital letter)
Vector는 소문자(Small letter)를 사용한다.

Machine Learning Model

Generative model

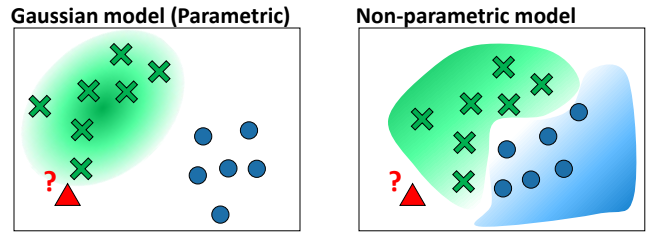
확률상 판단하는 모델
(가령, 개 같아? 고양이 같아?)

Non/Parametric 구분은 향후 확률과 통계 부분에서 추가 설명을 진행해보겠다.

Discriminative model

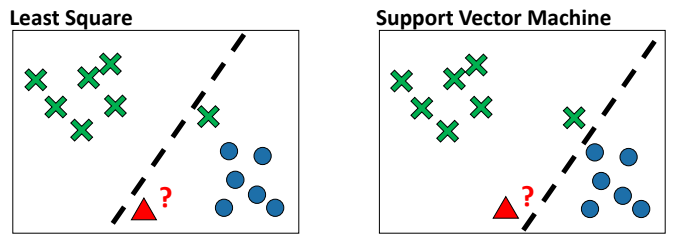
기냐 아니냐를 판단하는 모델 - find the line(model)
(가령, 강아지보다 고양이 같아? 고양이보다 강아지 같아?)

• Least Square : Norm과 연관
  여러 샘플들을 정확히 거리를 기반으로 절반을 나누는 모델을 찾는 방법이다.

• Support Vector Machine : Norm + a 와 연관
  모든 샘플을 고려하지 않고 가까운 샘플 두개를 고르고 가운데를 가로지르는 Decision boundary를 찾게 한다.

추후 다시 공부해본다.
상황에 따라 향 모델 중 선택을 하게 된다. 맞다 틀리다의 문제는 아니다.

Linear Model

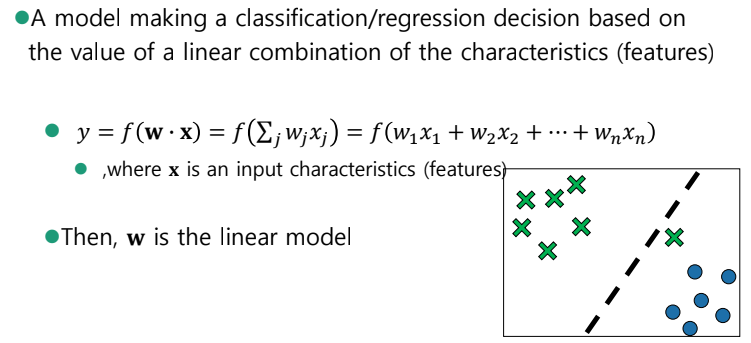
x = (x1, x2)

y = f >0, dog
y = f <0, cat

linear model은 결국 vector의 내적이다.

샘플이 여러개 있으면 vector가 쭈욱 쌓이고, 결국 이는 matrix로 표현되는 것이다.

y = f(W* X) W를 찾는 것이 주목적.

Linear Model - Classifier & Regressor

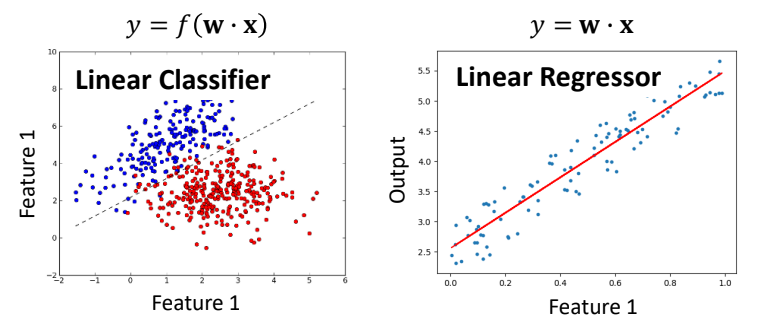
• Linear Classifier : f를 통해서 y의 값이 0 / 1로 바꿔주는 것
• Linear Regressor : 식의 결과값 자체가 label 값이 되는 경우

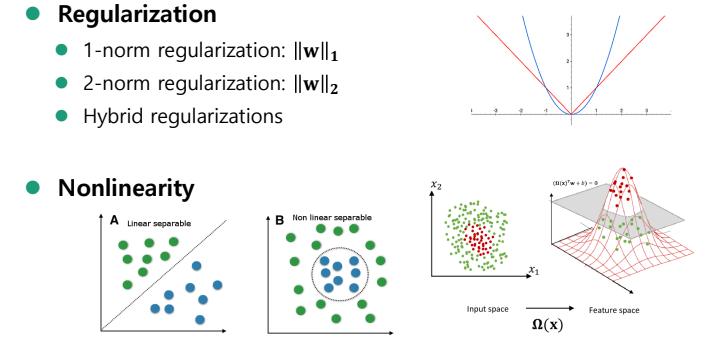
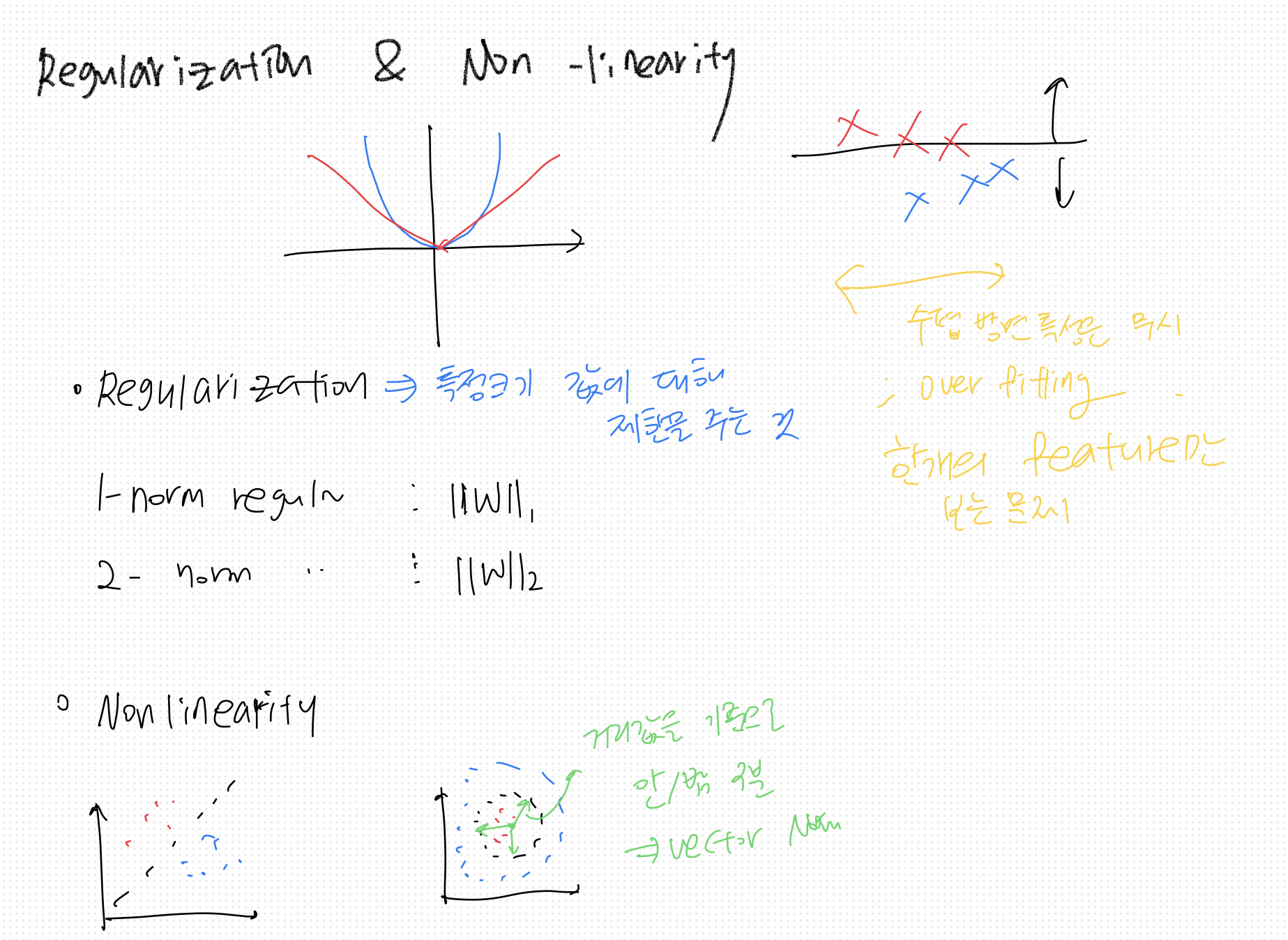
Regularization & Non-linearity