Week 3 | Hyperparameter Tuning
Tuning Process
- How do you go about finding a good setting for these hyperparameters?
- learning rate :
- momentum term : (good default is 0.9)
- the number of hidden units
- mini-batch size
- Adam Optimization Algorithm :
- learning rate decay
- the number of layers
red is most important,
followed orange,
followed purple,
But this isn't a hard and fast rule.
Other deep learning practitioners may disagree with me or have different intuitions on these.
- Now, if you're trying to tune some set of hyperparameters,
how do you select a set of values to explore?
Try random values : Don't use a grid
In earlier generations of machine learning algorithms,
if you had two hyperparameters(Hyperparameter 1, Hyperparameter 2) it was common practice to sample the points in a grid, and systematically explore these values.
In this example all 25 points, and then pick which of hyperparameter works best.
And this practice works okay when the number of hyperparamters was relatively small.
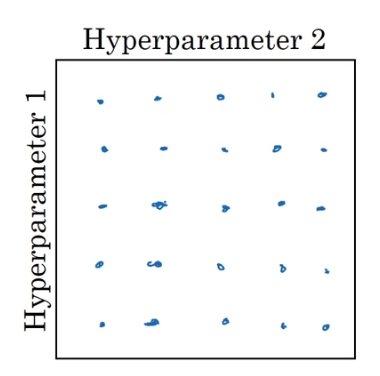
- Let's say Hyperparameter 1 turns out to be , the learning rate.
And let's say Hyperparameter 2 was that that you have in the denominator of the Adam algorithm.
So your choice of matters a lot than your choice of .
So if you sample in the gridthen you've really tried out 5 values of .
And you might find that all of the different values of give you essentially the same answer.
So you've now trained 25 models and only got into trial 5 values for the learning rate which i think is really important.
(더 중요한 hyperparameter인 는 5개의 옵션만 존재하기 때문에
25번의 model을 train시킬 동안 시도되는 는 5개 뿐이다.
따라서 최적의 를 찾기에는 한계가 있다.)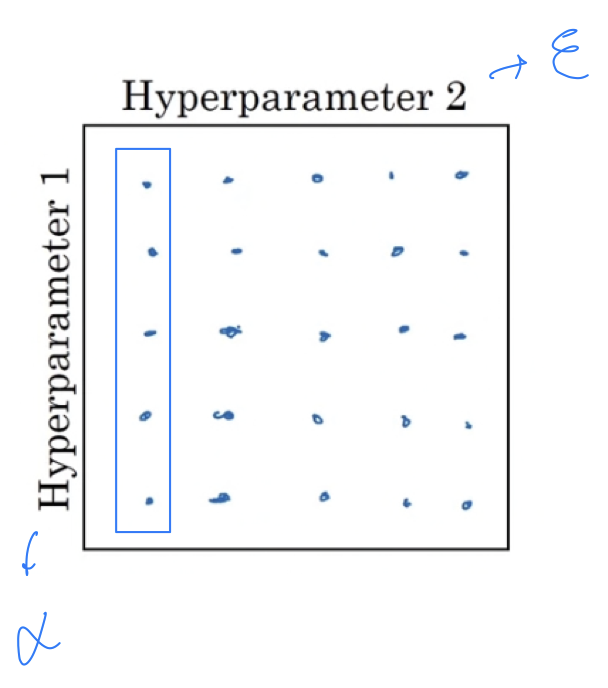
- Let's say Hyperparameter 1 turns out to be , the learning rate.
In deep learning, what we tend to do and what i recommend you do instead,
is choose the points at random.
So go ahead and choose a same number of points(=25 points),
and then try out the hyperparameters on this randomly chosen set of points.
The reason you do that is that it's difficult to know in advance
which hyperparameters are going to be the most important for your problem.
And some hyperparameters are actually much more important than others.
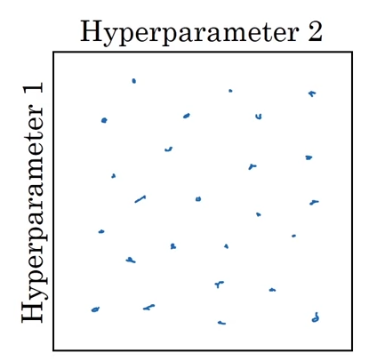
- Whereas in contrast,
if you were to sample atrandom, then you will have tried out 25 distinct values of the learning rate and therefore you be more likely to find a value that works really well.
(grid search에서는 25개의 model은 에 대해 5개의 값만 시도를 했었는데,
random search에서는 25개의 고유한 값을 시도하게 되므로
잘 작동하는 값을 찾을 가능성이 더 높아진다.)
If you have 3 Hyperparameters, you're searching over a cube.
By sampling this three-dimensional cube you get to try out a lot more values of each of your three hyperparameters.
And in practice you might be searching over even more hyperparameters than three and sometimes it's just hard to know in advance which ones turns out to be the really important hyperparamters for you application.
And sampling at random rather than in the grid shows that you are more richly exploring set of possible values for the most important hyperparamters.
- Whereas in contrast,
Coarse to fine
-
Another common practice is to use a
coarse to finesampling scheme. -
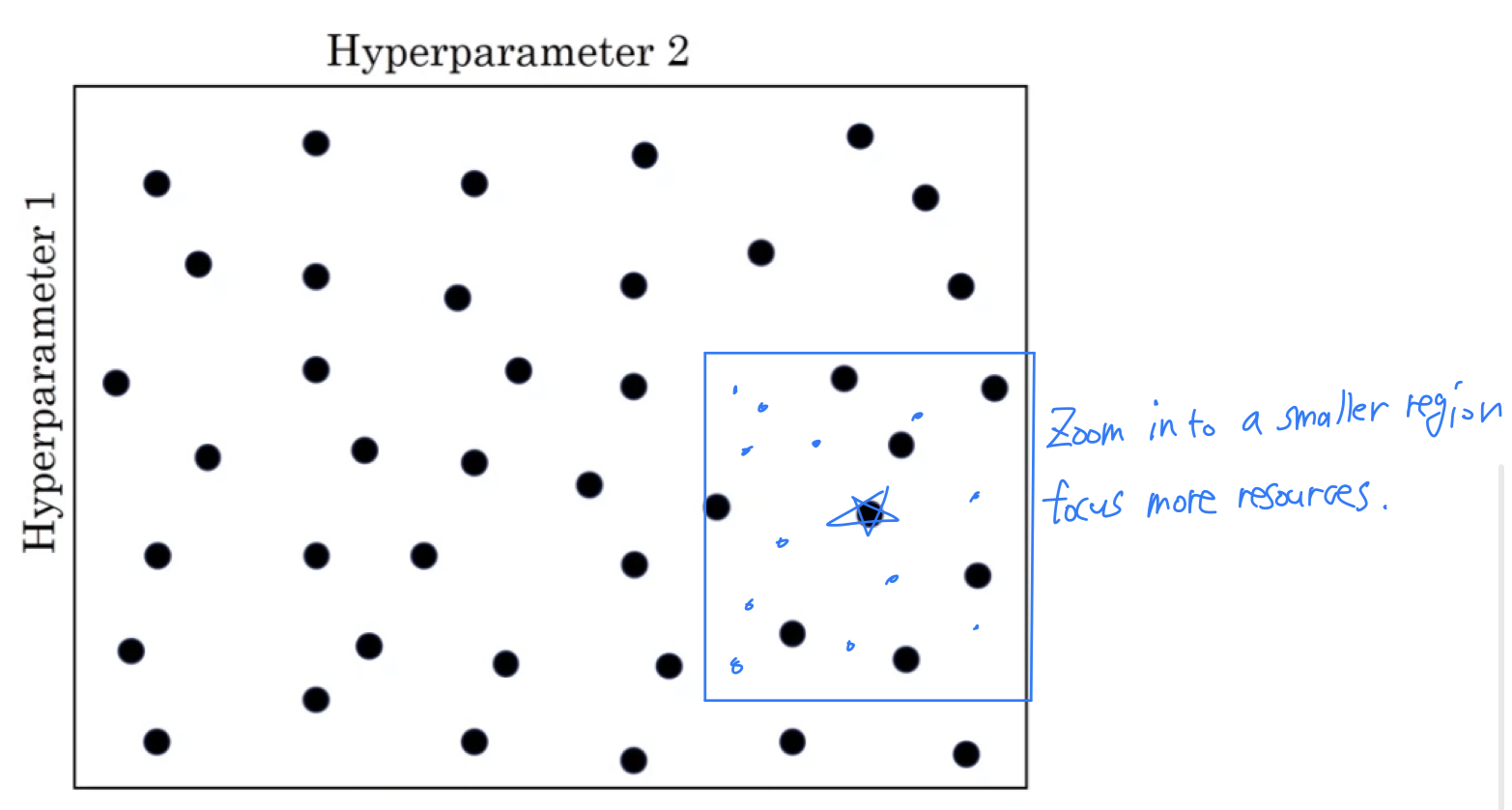
So let's say in this two-dimensional example that you sample these points,
and maybe you found that this point work the best and maybe a few other points around it tended to work really well.
Then inthe coarse of finescheme what you might do is zoom in to a smaller region of the hyperparamteres, and then sample more density within this space.
Or maybe again at rondom,
but to then focus more resources on searching within this blue square if you suspecting that the best set of the hyperparameters, may be in this region.
(최상의 설정인 하이퍼파라미터가 이 영역에 있을 수 있다고 의심되는 경우, 이 파란색 사각형 내에서 검색하는 데 더 많은 리소스를 집중할 수 있다.)
So after doing a coarse sample of this entire square, that tells you to then focus on a smaller square.
You can then sample more densely into smaller square.
(따라서 전체 사각형의 대략적인 sampling을 수행한 후,
더 작은 사각형으로 더 조밀하게 sampling할 수 있다.)
The two keys
1. Use random sampling
2. Optinally consider implementing a coarse to fine search process.
There's even more to hyperparameter search than these
Using an Appropriate Scale to pick Hyperparameters
- It's important to pick the appropriate scale on which to explore the hyperparameters.
Picking hyperparameters at random
- Let's say that you're trying to choose the number of hidden units, ,
and let's say that you think a good range of values is 50 ~ 100.
Maybe picking some number values at random within this number line.
Or if you're trying to decide on the number of layers in your nerual network, .
Maybe you think the total nubmer of layers should be 2~4.
Then sampling uniformly at random, along 2, 3 and 4 might be reasonable.
 So these were a couple examples where sampling
So these were a couple examples where sampling uniformlyat random over the range you're comtemplating might be a reasonable thing to do.
But this is not true for all hyperparameters.
(이러한 몇 가지 경우의 hyperparameter들은
균일화된 방법으로 샘플링하는 경우, 당신이 생각하고 있는 범위가 합리적인 방법일 수 있다.
하지만 이런 방법이 모든 hyperparameter에 적용되는 것은 아니다.)
Appropriate scale for hyperparameters
- Let's look at another example.
Say your searching for the hyperparameter , the learning rate.
And let's say that you suspect might be on the low end (낮은 경계선)
or maybe it could be as high as 1.
Sample values uniformly at random over this number line,
about 90% of the values you sample would be 0.1 ~ 1.
So you're using 90% of the resources to search 0.1 ~ 1
, and only 10% of the resources to search between 0.0001 ~ 0.1.
So that doesn't seem right.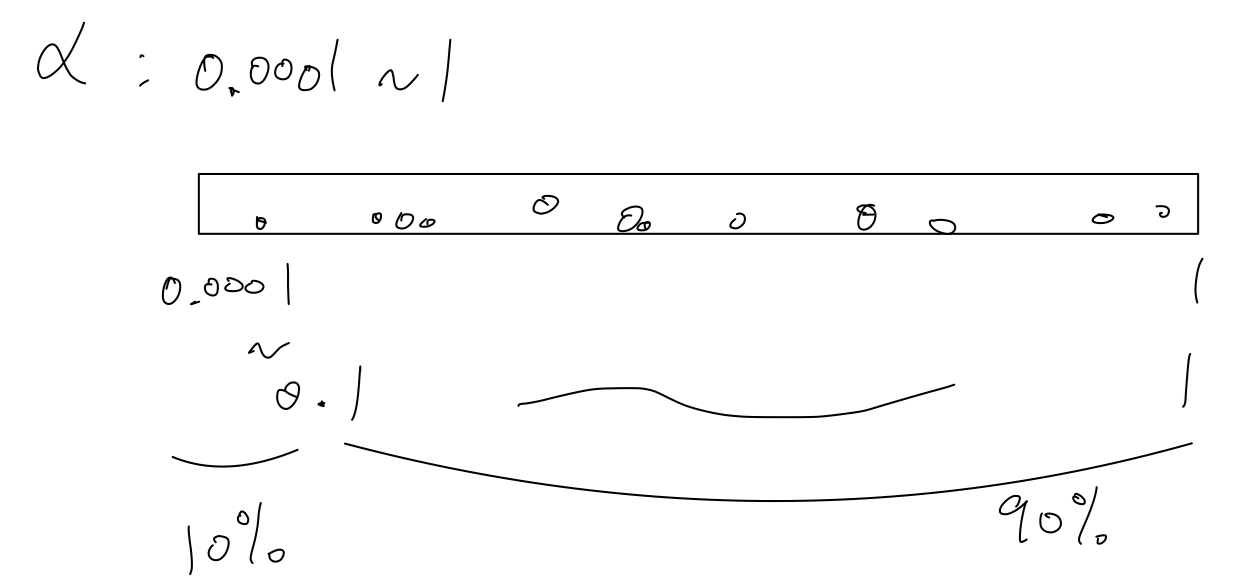 Instead, it seems more reason to search for hyperparameters on a
Instead, it seems more reason to search for hyperparameters on a log scale.
Instead of using a linear scale, you'd have 0.0001, 0.001, 0.01, 0.1, and then 1.
And you instead sample uniformly at random, on this tpye of logarithmic scale.
Now you have more resources dedicated to searching between 0.0001~0.001, and between 0.001 ~ 0.01, and so on.
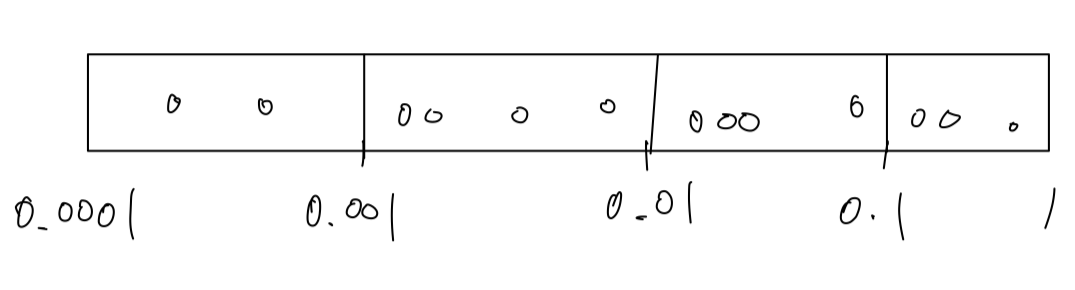 So in Python, the way you implement this,
So in Python, the way you implement this,
 In a more general case, if you're trying to sample between on the log scale
In a more general case, if you're trying to sample between on the log scale
what you do is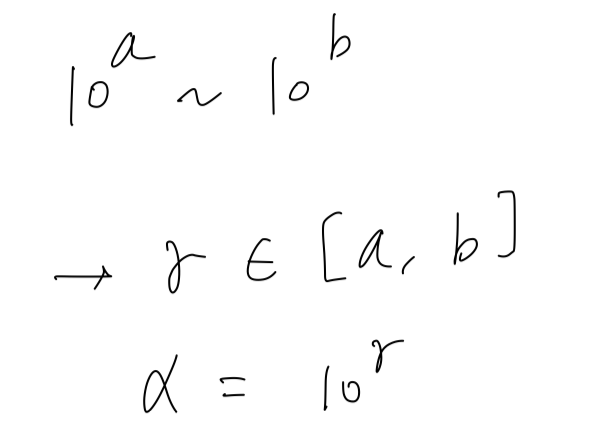 So that's how you implement sampling on this logarithmic scale.
So that's how you implement sampling on this logarithmic scale.
(이것이 log 척도의 sampling을 구현하는 방법이다.)
Hyperparameters for exponentially weighted averages
- Finally, one other tricky case is sampling the hyperparameter ,
used for computing exponentially weighted averages.
So let's say you suspect that should be somewhere between 0.9 ~ 0.999.
This is the range of values you want to search over.
So remember that, when computing exponentially weighted averaes using 0.9
is like averaging over the last 10 values
whereas using 0.999 is like averaging over the las 1,000 values.
So if you want to search between 0.9 ~ 0.999, it doesn't make sense to sample on the linear scale.(Uniformly at random between 0.9 ~ 0.9999)
So the best way to think about this,
is that we want to explore the range of values for
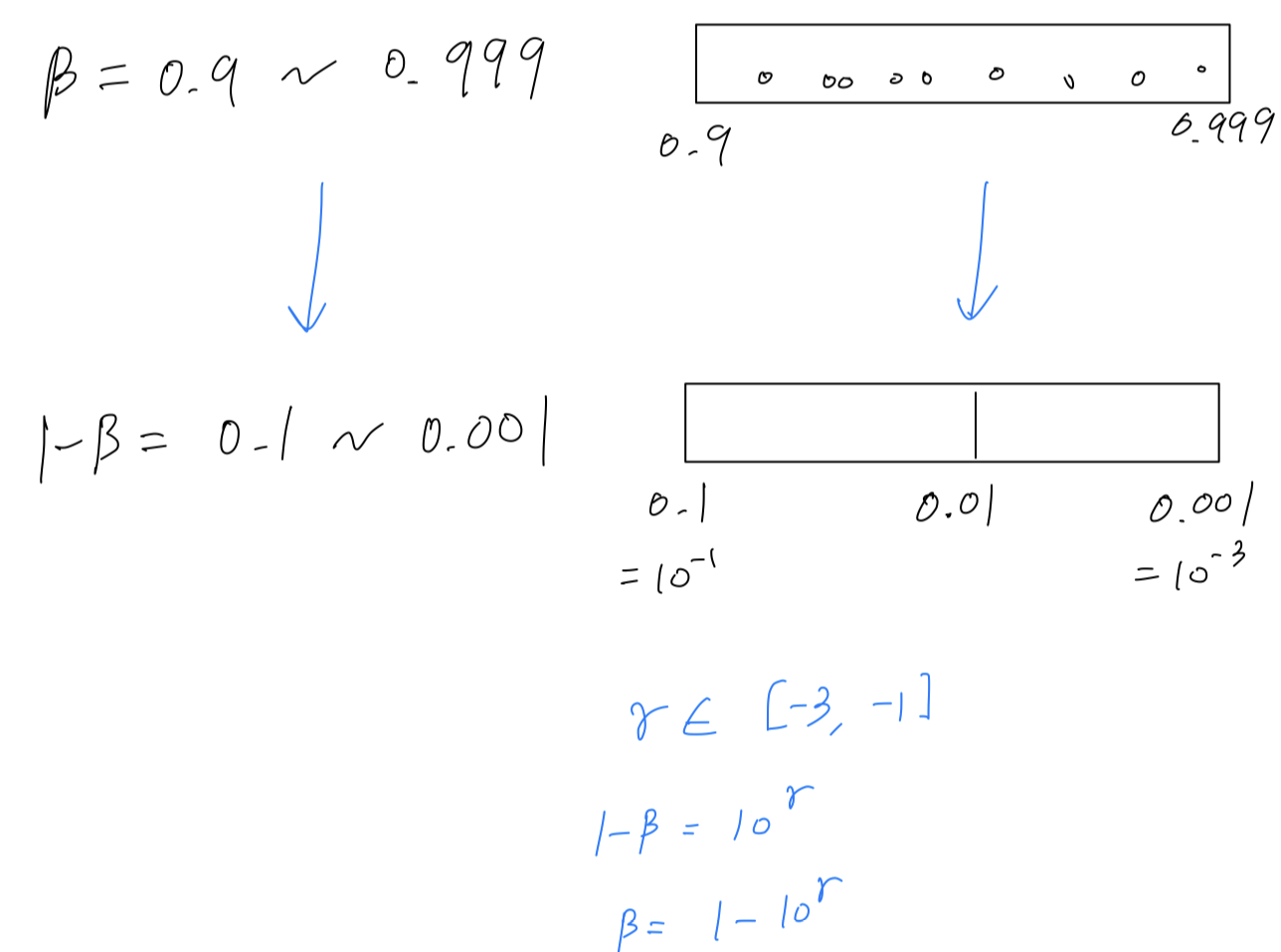 And hopefully this makes sense in that
And hopefully this makes sense in that
This way, you spend as much resources exploring the range 0.9 ~ 0.99 as
you would exploring 0.99 ~ 0.999.
So if you want to study more formal mathematical justification for why we're doing this
(why is it such a bad idea to sample in a linear scale?)
It is that, when ,
the senstivity of the results you get changes, even with very small changes to .
So if goes from 0.9 to 0.9005, it's no big deal, this is hardly any change in your results.
But if goes from 0.999 to 0.9995, this will have a huge impact on what your algorithm is doing.
And it's because that formula we have ,
this is very sensitive to small changes in when is close to .
So what this whole sampling process does, is it causes you to sample more densely in the region of when .
So that you can be more efficient in terms of how you distirbute the samples, to explore the space of possible outcomes more efficiently.
Hyperparameter Tuning in Practice : Pandas vs Caviar
-
Before wrapping up orur dicussion on hyperparamter search,
i want to share with you just a couple of final tips and tricks for how to organize your hyperparamter search process. -
Deep learning today is applied to many different application areas and
that intuitions about hyperparameter settings from one application area
may or may not transfer to a different one. -
Finally, in terms of
how people go about searching for hyperparameters,
i see maybetwo major different waysin which people go about it.
1. Babysitting one model
- One way is if you
babysit one model.
(하나의 modeldmf ehfqhsms rjt)
Usually you do this if you have maybe a huge data set
but not a lot of computational resourecs, not a lot of CPUs and GPUs,
so you can basically afford to train only one model or a very small number of models at a time.
In that case you might gradually babysit that model even as it's training.
(dataset은 매우 크지만 CPU와 CPU 자원과 같은 것들이 충분치 않아서
보통한 번에 하나의 model만 train시킬 수 있다.
이러한 경우, 우리는 해당 model이 train되는 동안 계속해서 돌봐줄 수 있다.)
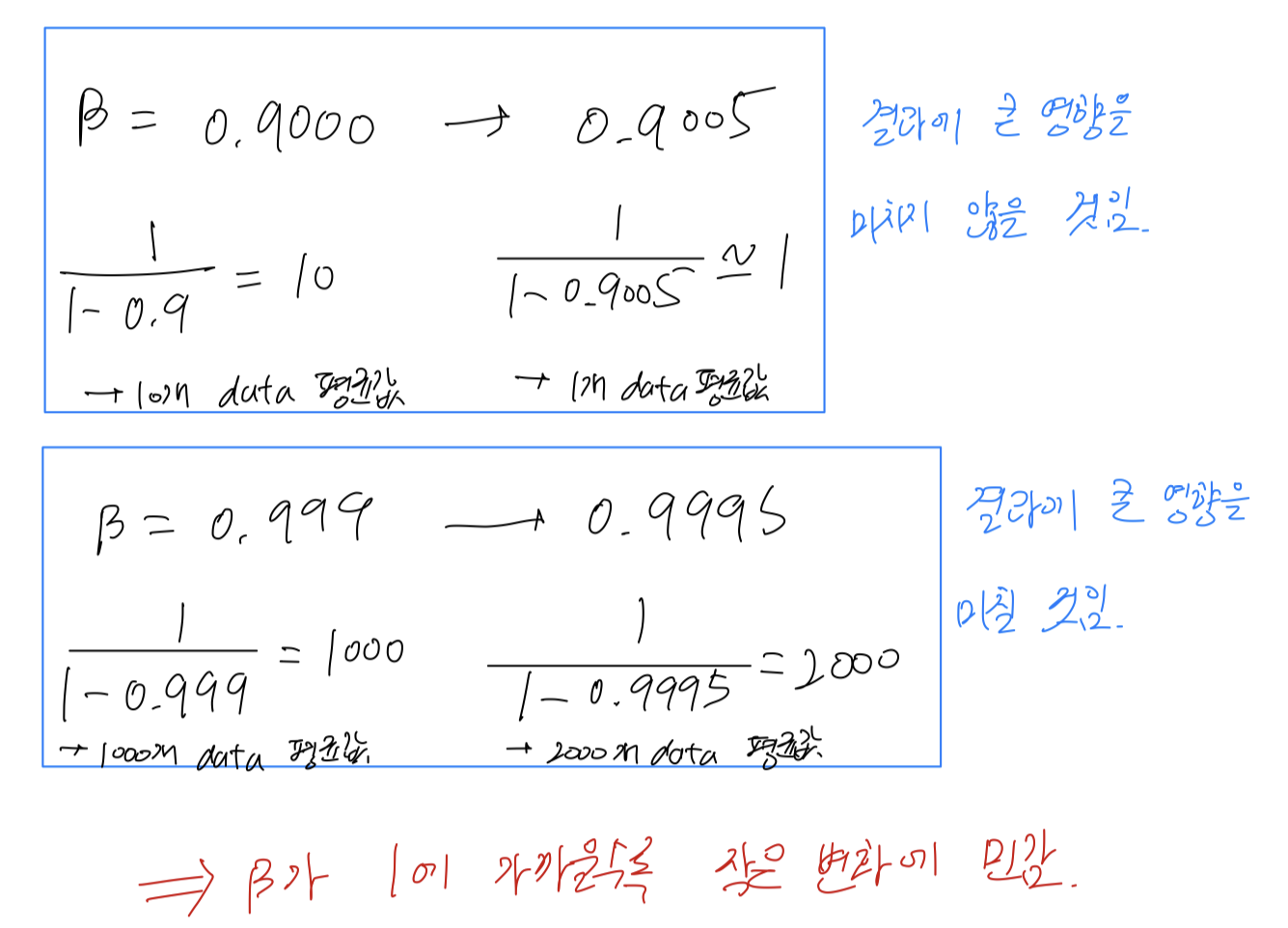
So, for example, on Day 0 you might initialize your parameter as random and then start training.
And you gradually watch your learning curve, maybe the cost function gradually decrease over the first day.
Then at the end of Day 1, you might say " looks it's learning quite well. I'm going to try increasing the learning rate a little bit and see how it does."
And then maybe it does better.
And after 2 days you say "Okay it's still doing quite well. Maybe i'll fill the momentum term a bit or decrease the learning variable a bit now."
and then you're now into Day 3.
And every day you kind of look at it and try nudging up and down your paramters.
And maybe on one day you found your learning rate was too big.
So you might go back to the previous day's model, and so on.
이러한 방법이 Babysitting one model이고, 동시에 여러 model을 train시킬 충분한 resource가 되지 않는 경우에 사용하는 방법이다. - So to make an analogy,
Babysitting one modelis going to call thepanda approach.
When pandas have childeren they have very few children, usually one child at a time.
Then they really put a lot of efforts into making sure that the baby panda survives.
2. Training many models in parallel.
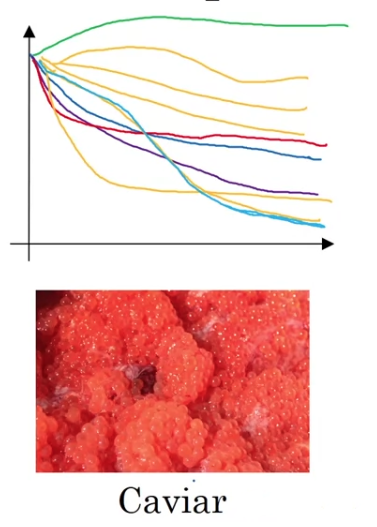
- The other approach would be if you train many models in parallel.
So you might have some setting of the hyperparameters and
just let it run by itself,
either for a day even for multiple days, and then you get some learning curve.
And then at the same time you might start up a different model with a different setting of the hyperparameters.
And so, your second model might generate a different learning curve.
And at the same time, you might train a third model.
And another one that maybe this diverges.
Or you might train many different models in parallel.
This way you can try a lot of different hyperparameter settings and then quickly at the end pick the one that works best. - Whereas
Training many models in parallelis going to call theCaviar strategy.
There's some fish that lay over 100 millon eggs in one mating season.
They lay a log of eggs and don'y pay too much attention to any one of them
just see that hopefully one of them will do well.
If you have enough computers to train a lot of models in parallel,
then by all means take the cavier approach and try a lot of different hyperparameters and see what works.
But in some application domains(online advertising setting, computer vision) where there's so much data and the models you want to train is so big that it's difficult to train a lot of models at the same time.
I've seen those communities use the panda approach a little bit more.
이런 유용한 정보를 나눠주셔서 감사합니다.